In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the rate of change of a function. These applications include acceleration and velocity in physics, population growth rates in biology, and marginal functions in economics.
One application for derivatives is to estimate an unknown value of a function at a point by using a known value of a function at some given point together with its rate of change at the given point. If
is a function defined on an interval
then the amount of change of
over the interval is the change in the
values of the function over that interval and is given by
The average rate of change of the function
over that same interval is the ratio of the amount of change over that interval to the corresponding change in the
values. It is given by
As we already know, the instantaneous rate of change of
at
is its derivative
For small enough values of
We can then solve for
to get the amount of change formula:
We can use this formula if we know only
and
and wish to estimate the value of
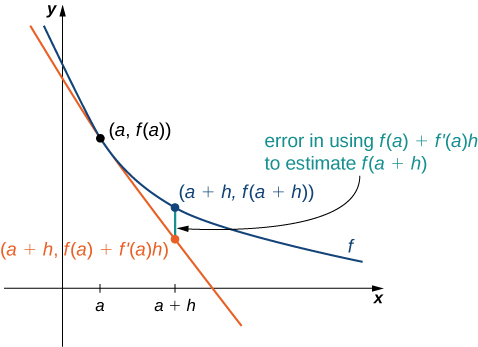
For example, we may use the current population of a city and the rate at which it is growing to estimate its population in the near future. As we can see in [link], we are approximating
by the
coordinate at
on the line tangent to
at
Observe that the accuracy of this estimate depends on the value of
as well as the value of

Here is an interesting demonstration of rate of change.
If
and
estimate
Begin by finding
We have
Thus,
Given
and
estimate
Use the same process as in the preceding example.
Another use for the derivative is to analyze motion along a line. We have described velocity as the rate of change of position. If we take the derivative of the velocity, we can find the acceleration, or the rate of change of velocity. It is also important to introduce the idea of speed, which is the magnitude of velocity. Thus, we can state the following mathematical definitions.
Let
be a function giving the position of an object at time
The velocity of the object at time
is given by
The speed of the object at time
is given by
The acceleration of the object at
is given by
A ball is dropped from a height of 64 feet. Its height above ground (in feet)
seconds later is given by
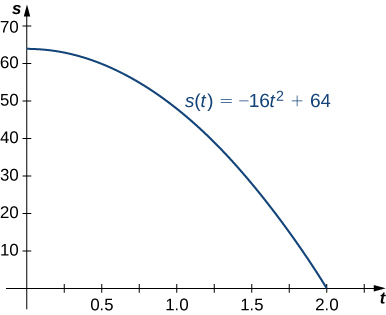
The first thing to do is determine how long it takes the ball to reach the ground. To do this, set
Solving
we get
so it take 2 seconds for the ball to reach the ground.
Since
we obtain
A particle moves along a coordinate axis in the positive direction to the right. Its position at time
is given by
Find
and
and use these values to answer the following questions.
Begin by finding
and
and
Evaluating these functions at
we obtain
and
the particle is moving from right to left.
and
velocity and acceleration are acting in opposite directions. In other words, the particle is being accelerated in the direction opposite the direction in which it is traveling, causing
to decrease. The particle is slowing down.
The position of a particle moving along a coordinate axis is given by
so set
Factoring the left-hand side of the equation produces
Solving, we find that the particle is at rest at
and
and from right to left when
[link] gives the analysis of the sign of
for
but it does not represent the axis along which the particle is moving.

Since
on
the particle is moving from left to right on these intervals.
Since
on
the particle is moving from right to left on this interval.
and at the times that it changes direction
We have
and
This means that the particle begins on the coordinate axis at 4 and changes direction at 0 and 20 on the coordinate axis. The path of the particle is shown on a coordinate axis in [link]. 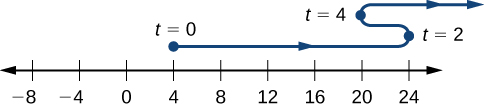
A particle moves along a coordinate axis. Its position at time
is given by
Is the particle moving from right to left or from left to right at time
left to right
Find
and look at the sign.
In addition to analyzing velocity, speed, acceleration, and position, we can use derivatives to analyze various types of populations, including those as diverse as bacteria colonies and cities. We can use a current population, together with a growth rate, to estimate the size of a population in the future. The population growth rate is the rate of change of a population and consequently can be represented by the derivative of the size of the population.
If
is the number of entities present in a population, then the population growth rate of
is defined to be
The population of a city is tripling every 5 years. If its current population is 10,000, what will be its approximate population 2 years from now?
Let
be the population (in thousands)
years from now. Thus, we know that
and based on the information, we anticipate
Now estimate
the current growth rate, using
By applying [link] to
we can estimate the population 2 years from now by writing
thus, in 2 years the population will be 18,000.
The current population of a mosquito colony is known to be 3,000; that is,
If
estimate the size of the population in 3 days, where
is measured in days.
3,300
Use
In addition to analyzing motion along a line and population growth, derivatives are useful in analyzing changes in cost, revenue, and profit. The concept of a marginal function is common in the fields of business and economics and implies the use of derivatives. The marginal cost is the derivative of the cost function. The marginal revenue is the derivative of the revenue function. The marginal profit is the derivative of the profit function, which is based on the cost function and the revenue function.
If
is the cost of producing x items, then the marginal cost
is
If
is the revenue obtained from selling
items, then the marginal revenue
is
If
is the profit obtained from selling x items, then the marginal profit
is defined to be
We can roughly approximate
by choosing an appropriate value for
Since x represents objects, a reasonable and small value for
is 1. Thus, by substituting
we get the approximation
Consequently,
for a given value of
can be thought of as the change in cost associated with producing one additional item. In a similar way,
approximates the revenue obtained by selling one additional item, and
approximates the profit obtained by producing and selling one additional item.
Assume that the number of barbeque dinners that can be sold,
can be related to the price charged,
by the equation
In this case, the revenue in dollars obtained by selling
barbeque dinners is given by
Use the marginal revenue function to estimate the revenue obtained from selling the 101st barbeque dinner. Compare this to the actual revenue obtained from the sale of this dinner.
First, find the marginal revenue function:
Next, use
to approximate
the revenue obtained from the sale of the 101st dinner. Since
the revenue obtained from the sale of the 101st dinner is approximately $3.
The actual revenue obtained from the sale of the 101st dinner is
The marginal revenue is a fairly good estimate in this case and has the advantage of being easy to compute.
Suppose that the profit obtained from the sale of
fish-fry dinners is given by
Use the marginal profit function to estimate the profit from the sale of the 101st fish-fry dinner.
$2
Use
to approximate
it is possible to estimate
given
and
For the following exercises, the given functions represent the position of a particle traveling along a horizontal line.
a.
b. speeds up
slows down
A rocket is fired vertically upward from the ground. The distance
in feet that the rocket travels from the ground after
seconds is given by
a.
b.
A ball is thrown downward with a speed of 8 ft/s from the top of a 64-foot-tall building. After t seconds, its height above the ground is given by
The position function
represents the position of the back of a car backing out of a driveway and then driving in a straight line, where
is in feet and
is in seconds. In this case,
represents the time at which the back of the car is at the garage door, so
is the starting position of the car, 4 feet inside the garage.
a. 5 ft/s b. 9 ft/s
The position of a hummingbird flying along a straight line in
seconds is given by
meters.
sec.
sec.
A potato is launched vertically upward with an initial velocity of 100 ft/s from a potato gun at the top of an 85-foot-tall building. The distance in feet that the potato travels from the ground after
seconds is given by
and
a. 84 ft/s, −84 ft/s b. 84 ft/s c.
d.
in both cases e.
f.
The position function
gives the position in miles of a freight train where east is the positive direction and
is measured in hours.
The following graph shows the position
of an object moving along a straight line.
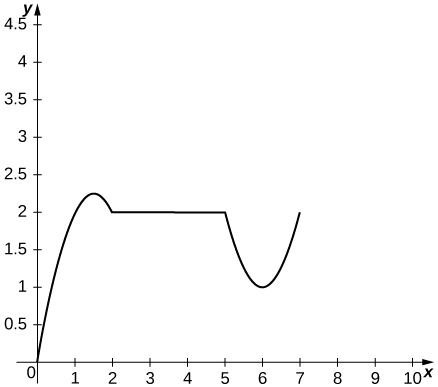
a. Velocity is positive on
negative on
and zero on
b.* * *
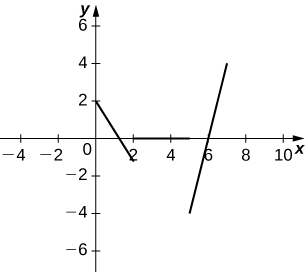
c. Acceleration is positive on
negative on
and zero on
d. The object is speeding up on
and slowing down on
The cost function, in dollars, of a company that manufactures food processors is given by
where
is the number of food processors manufactured.
The price
(in dollars) and the demand
for a certain digital clock radio is given by the price–demand function
and
a.
b.
c. $6 per item, $0 per item
[T] A profit is earned when revenue exceeds cost. Suppose the profit function for a skateboard manufacturer is given by
where
is the number of skateboards sold.
[T] In general, the profit function is the difference between the revenue and cost functions:
Suppose the price-demand and cost functions for the production of cordless drills is given respectively by
and
where
is the number of cordless drills that are sold at a price of
dollars per drill and
is the cost of producing
cordless drills.
and
Interpret the results.
and
Interpret the results.
a.
b.
c.
At a production level of 1000 cordless drills, revenue is increasing at a rate of $83 per drill; at a production level of 4000 cordless drills, revenue is decreasing at a rate of $97 per drill. d.
e.
At a production level of 1000 cordless drills, profit is increasing at a rate of $18 per drill; at a production level of 4000 cordless drills, profit is decreasing at a rate of $162 per drill.
A small town in Ohio commissioned an actuarial firm to conduct a study that modeled the rate of change of the town’s population. The study found that the town’s population (measured in thousands of people) can be modeled by the function
where
is measured in years.
of the population function.
and
Interpret what the results mean for the town.
and
Interpret what the results mean for the town’s population.
[T] A culture of bacteria grows in number according to the function
where
is measured in hours.
and
and
Interpret what the answers imply about the bacteria population growth.
a.
b.
c. The bacteria population increases from time 0 to 10 hours; afterwards, the bacteria population decreases. d.
The rate at which the bacteria is increasing is decreasing during the first 10 hours. Afterwards, the bacteria population is decreasing at a decreasing rate.
The centripetal force of an object of mass
is given by
where
is the speed of rotation and
is the distance from the center of rotation.
The following questions concern the population (in millions) of London by decade in the 19th century, which is listed in the following table.
| Years since 1800 | Population (millions) |
|---|---|
| 1 | 0.8795 |
| 11 | 1.040 |
| 21 | 1.264 |
| 31 | 1.516 |
| 41 | 1.661 |
| 51 | 2.000 |
| 61 | 2.634 |
| 71 | 3.272 |
| 81 | 3.911 |
| 91 | 4.422 |
[T]
a.
b.
The population is increasing. c.
The rate at which the population is increasing is constant.
[T]
For the following exercises, consider an astronaut on a large planet in another galaxy. To learn more about the composition of this planet, the astronaut drops an electronic sensor into a deep trench. The sensor transmits its vertical position every second in relation to the astronaut’s position. The summary of the falling sensor data is displayed in the following table.
| Time after dropping (s) | Position (m) | {: valign=”top”}|———- | 0 | 0 | {: valign=”top”}| 1 | −1 | {: valign=”top”}| 2 | −2 | {: valign=”top”}| 3 | −5 | {: valign=”top”}| 4 | −7 | {: valign=”top”}| 5 | −14 | {: valign=”top”}{: .unnumbered summary=”This table has seven rows and two columns. The first row is a header row and it labels each column. The first column header is Time after dropping (s) and the second column is Position (m). Under the first column are the values 0, 1, 2, 3, 4, and 5. Under the second column are the values 0, −1, −2, −5, −7, and −14.” data-label=””}
[T]
a.
b.
This is the velocity of the sensor. c.
This is the acceleration of the sensor; it is a constant acceleration downward.
[T]
The following problems deal with the Holling type I, II, and III equations. These equations describe the ecological event of growth of a predator population given the amount of prey available for consumption.
[T] The Holling type I equation is described by
where
is the amount of prey available and
is the rate at which the predator meets the prey for consumption.
a.* * *
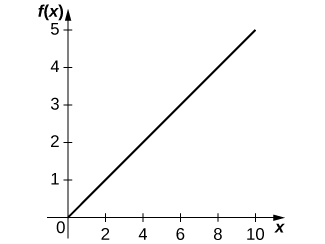
b.
The more increase in prey, the more growth for predators. c.
As the amount of prey increases, the rate at which the predator population growth increases is constant. d. This equation assumes that if there is more prey, the predator is able to increase consumption linearly. This assumption is unphysical because we would expect there to be some saturation point at which there is too much prey for the predator to consume adequately.
[T] The Holling type II equation is described by
where
is the amount of prey available and
is the maximum consumption rate of the predator.
and
What are the differences between the Holling type I and II equations?
and interpret the meaning of the parameter
[T] The Holling type III equation is described by
where
is the amount of prey available and
is the maximum consumption rate of the predator.
and
What are the differences between the Holling type II and III equations?
a.* * *
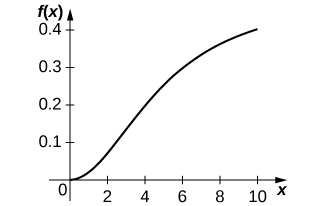
b.
When the amount of prey increases, the predator growth increases. c.
When the amount of prey is extremely small, the rate at which predator growth is increasing is increasing, but when the amount of prey reaches above a certain threshold, the rate at which predator growth is increasing begins to decrease. d. At lower levels of prey, the prey is more easily able to avoid detection by the predator, so fewer prey individuals are consumed, resulting in less predator growth.
[T] The populations of the snowshoe hare (in thousands) and the lynx (in hundreds) collected over 7 years from 1937 to 1943 are shown in the following table. The snowshoe hare is the primary prey of the lynx.
| Population of snowshoe hare (thousands) | Population of lynx (hundreds) |
|---|---|
| 20 | 10 |
| 55 | 15 |
| 65 | 55 |
| 95 | 60 |
and
determine values for those parameters by examining a graph of the data. Recall that
measures what prey value results in the half-maximum of the predator value.
over an interval
is
over an interval
is
is the speed of an object at time
whose velocity is given by

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: