By now you have progressed from the very informal definition of a limit in the introduction of this chapter to the intuitive understanding of a limit. At this point, you should have a very strong intuitive sense of what the limit of a function means and how you can find it. In this section, we convert this intuitive idea of a limit into a formal definition using precise mathematical language. The formal definition of a limit is quite possibly one of the most challenging definitions you will encounter early in your study of calculus; however, it is well worth any effort you make to reconcile it with your intuitive notion of a limit. Understanding this definition is the key that opens the door to a better understanding of calculus.
Before stating the formal definition of a limit, we must introduce a few preliminary ideas. Recall that the distance between two points a and b on a number line is given by
may be interpreted as: *The distance between
and L is less than ε.*
may be interpreted as:
and the distance between x and a is less than δ.
It is also important to look at the following equivalences for absolute value:
is equivalent to the statement
is equivalent to the statement
and
With these clarifications, we can state the formal epsilon-delta definition of the limit.
Let
be defined for all
over an open interval containing a. Let L be a real number. Then
if, for every
there exists a
such that if
then
This definition may seem rather complex from a mathematical point of view, but it becomes easier to understand if we break it down phrase by phrase. The statement itself involves something called a universal quantifier (for every
an existential quantifier (there exists a
and, last, a conditional statement (if
then
Let’s take a look at [link], which breaks down the definition and translates each part.
| Definition | Translation |
|---|---|
| 1. For every | 1. For every positive distance ε from L, |
| 2. there exists a | 2. There is a positive distance from a, |
| 3. such that | 3. such that |
| 4. if then | 4. if x is closer than to a and then is closer than ε to L. |
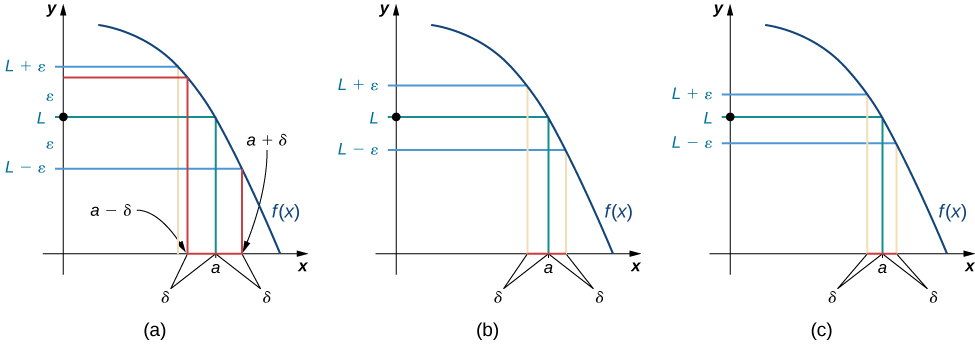
We can get a better handle on this definition by looking at the definition geometrically. [link] shows possible values of
for various choices of
for a given function
a number a, and a limit L at a. Notice that as we choose smaller values of ε (the distance between the function and the limit), we can always find a
small enough so that if we have chosen an x value within
of a, then the value of
is within ε of the limit L.

Visit the following applet to experiment with finding values of
for selected values of ε:
[link] shows how you can use this definition to prove a statement about the limit of a specific function at a specified value.
Prove that
Let
The first part of the definition begins “For every
This means we must prove that whatever follows is true no matter what positive value of ε is chosen. By stating “Let
we signal our intent to do so.
Choose
The definition continues with “there exists a
” The phrase “there exists” in a mathematical statement is always a signal for a scavenger hunt. In other words, we must go and find
So, where exactly did
come from? There are two basic approaches to tracking down
One method is purely algebraic and the other is geometric.
We begin by tackling the problem from an algebraic point of view. Since ultimately we want
we begin by manipulating this expression:
is equivalent to
which in turn is equivalent to
Last, this is equivalent to
Thus, it would seem that
is appropriate.
We may also find
through geometric methods. [link] demonstrates how this is done.
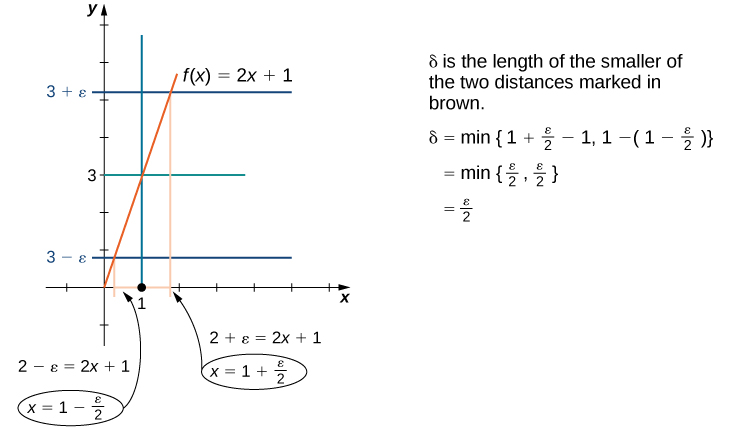
Assume
When
has been chosen, our goal is to show that if
then
To prove any statement of the form “If this, then that,” we begin by assuming “this” and trying to get “that.”
Thus,
In this part of the proof, we started with
and used our assumption
in a key part of the chain of inequalities to get
to be less than ε. We could just as easily have manipulated the assumed inequality
to arrive at
as follows:
Therefore,
(Having completed the proof, we state what we have accomplished.)
After removing all the remarks, here is a final version of the proof:
Let
Choose
Assume
Thus,
Therefore,
The following Problem-Solving Strategy summarizes the type of proof we worked out in [link].
After we have obtained this value, we make the following statement, filling in the blank with our choice of
: Choose
Assume
where
and L are our function
and our limit L. At some point, we need to use
Complete the proof that
by filling in the blanks.
Let _____.
Choose
Assume
Thus,
We begin by filling in the blanks where the choices are specified by the definition. Thus, we have
Let
Choose
Assume
(or equivalently,
Thus,
Focusing on the final line of the proof, we see that we should choose
We now complete the final write-up of the proof:
Let
Choose
Assume
(or equivalently,
Thus,
Complete the proof that
by filling in the blanks.
Let _______.
Choose
Assume
Thus,
Therefore,
Let
choose
assume
Thus,
Therefore,
Follow the outline in the Problem-Solving Strategy that we worked out in full in [link].
In [link] and [link], the proofs were fairly straightforward, since the functions with which we were working were linear. In [link], we see how to modify the proof to accommodate a nonlinear function.
Prove that
The first part of the definition begins “For every
so we must prove that whatever follows is true no matter what positive value of ε is chosen. By stating “Let
we signal our intent to do so.
Two questions present themselves: Why do we want
and why is it okay to make this assumption? In answer to the first question: Later on, in the process of solving for
we will discover that
involves the quantity
Consequently, we need
In answer to the second question: If we can find
that “works” for
then it will “work” for any
as well. Keep in mind that, although it is always okay to put an upper bound on ε, it is never okay to put a lower bound (other than zero) on ε.
[link] shows how we made this choice of
![This graph shows how we find δ geometrically for a given ε for the proof in [link]. This graph shows how to find delta geometrically for a given epsilon for the above proof. First, the function f(x) = x^2 is drawn from [-1, 3]. On the y axis, the proposed limit 4 is marked, and the line y=4 is drawn to intersect with the function at (2,4). For a given epsilon, point 4 + epsilon and 4 – epsilon are marked on the y axis above and below 4. Blue lines are drawn from these points to intersect with the function, where pink lines are drawn from the point of intersection to the x axis. These lines land on either side of x=2. Next, we solve for these x values, which have to be positive here. The first is x^2 = 4 – epsilon, which simplifies to x = sqrt(4-epsilon). The next is x^2 = 4 + epsilon, which simplifies to x = sqrt(4 + epsilon). Delta is the smaller of the two distances, so it is the min of (2 – sqrt(4 – epsilon) and sqrt(4 + epsilon) – 2).](../resources/CNX_Calc_Figure_02_05_003.jpg)
then
so we must begin by assuming
We don’t really need
(in other words,
for this proof. Since
it is okay to drop
Hence,
Recall that
Thus,
and consequently
We also use
here. We might ask at this point: Why did we substitute
for
on the left-hand side of the inequality and
on the right-hand side of the inequality? If we look at [link], we see that
corresponds to the distance on the left of 2 on the x-axis and
corresponds to the distance on the right. Thus,
We simplify the expression on the left:
Then, we add 2 to all parts of the inequality:
We square all parts of the inequality. It is okay to do so, since all parts of the inequality are positive:
We subtract 4 from all parts of the inequality:
Last,
The geometric approach to proving that the limit of a function takes on a specific value works quite well for some functions. Also, the insight into the formal definition of the limit that this method provides is invaluable. However, we may also approach limit proofs from a purely algebraic point of view. In many cases, an algebraic approach may not only provide us with additional insight into the definition, it may prove to be simpler as well. Furthermore, an algebraic approach is the primary tool used in proofs of statements about limits. For [link], we take on a purely algebraic approach.
Prove that
Let’s use our outline from the Problem-Solving Strategy:
This choice of
may appear odd at first glance, but it was obtained by taking a look at our ultimate desired inequality:
This inequality is equivalent to
At this point, the temptation simply to choose
is very strong. Unfortunately, our choice of
must depend on ε only and no other variable. If we can replace
by a numerical value, our problem can be resolved. This is the place where assuming
comes into play. The choice of
here is arbitrary. We could have just as easily used any other positive number. In some proofs, greater care in this choice may be necessary. Now, since
and
we are able to show that
Consequently,
At this point we realize that we also need
Thus, we choose
Thus,
Since
we may conclude that
Thus, by subtracting 4 from all parts of the inequality, we obtain
Consequently,
This gives us
Therefore,
Complete the proof that
Let
choose
assume
Since
we may conclude that
Thus,
Hence,
Use [link] as a guide.
You will find that, in general, the more complex a function, the more likely it is that the algebraic approach is the easiest to apply. The algebraic approach is also more useful in proving statements about limits.
We now demonstrate how to use the epsilon-delta definition of a limit to construct a rigorous proof of one of the limit laws. The triangle inequality is used at a key point of the proof, so we first review this key property of absolute value.
The triangle inequality states that if a and b are any real numbers, then
We prove the following limit law: If
and
then
Let
Choose
so that if
then
Choose
so that if
then
Choose
Assume
Thus,
Hence,
□
We now explore what it means for a limit not to exist. The limit
does not exist if there is no real number L for which
Thus, for all real numbers L,
To understand what this means, we look at each part of the definition of
together with its opposite. A translation of the definition is given in [link].
| Definition | Opposite |
|---|---|
| 1. For every | 1. There exists so that |
| 2. there exists a so that | 2. for every |
| 3. if then | 3. There is an x satisfying so that |
Finally, we may state what it means for a limit not to exist. The limit
does not exist if for every real number L, there exists a real number
so that for all
there is an x satisfying
so that
Let’s apply this in [link] to show that a limit does not exist.
Show that
does not exist. The graph of
is shown here:
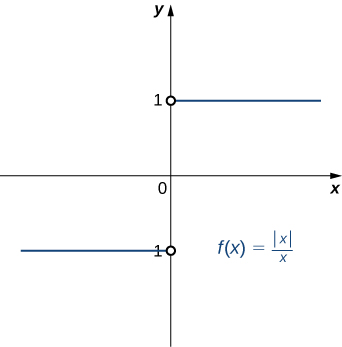
Suppose that L is a candidate for a limit. Choose
Let
Either
or
If
then let
Thus,
and
On the other hand, if
then let
Thus,
and
Thus, for any value of L,
Just as we first gained an intuitive understanding of limits and then moved on to a more rigorous definition of a limit, we now revisit one-sided limits. To do this, we modify the epsilon-delta definition of a limit to give formal epsilon-delta definitions for limits from the right and left at a point. These definitions only require slight modifications from the definition of the limit. In the definition of the limit from the right, the inequality
replaces
which ensures that we only consider values of x that are greater than (to the right of) a. Similarly, in the definition of the limit from the left, the inequality
replaces
which ensures that we only consider values of x that are less than (to the left of) a.
Limit from the Right: Let
be defined over an open interval of the form
where
Then,
if for every
there exists a
such that if
then
Limit from the Left: Let
be defined over an open interval of the form
where
Then,
if for every
there exists a
such that if
then
Prove that
Let
Choose
Since we ultimately want
we manipulate this inequality to get
or, equivalently,
making
a clear choice. We may also determine
geometrically, as shown in [link].
![This graph shows how we find δ for the proof in [link]. A graph showing how to find delta for the above proof. The function f(x) = sqrt(x-4) is drawn for x > 4. Since the proposed limit is 0, lines y = 0 + epsilon and y = 0 – epsilon are drawn in blue. Since only the top blue line corresponding to y = 0 + epsilon intersects the function, one red line is drawn from the point of intersection to the x axis. This x value is found by solving sqrt(x-4) = epsilon, or x = epsilon squared + 4. Delta is then the distance between this point and 4, which is epsilon squared.](../resources/CNX_Calc_Figure_02_05_004.jpg)
Assume
Thus,
Hence,
Finally,
Therefore,
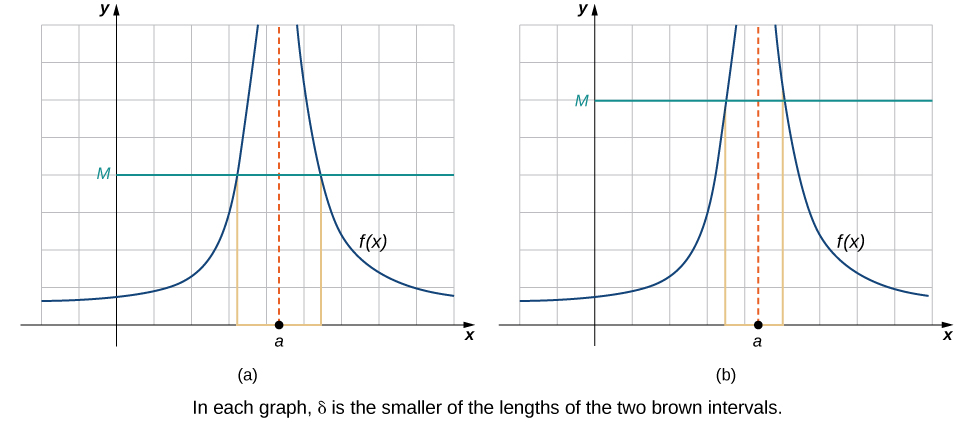
We conclude the process of converting our intuitive ideas of various types of limits to rigorous formal definitions by pursuing a formal definition of infinite limits. To have
we want the values of the function
to get larger and larger as x approaches a. Instead of the requirement that
for arbitrarily small ε when
for small enough
we want
for arbitrarily large positive M when
for small enough
[link] illustrates this idea by showing the value of
for successively larger values of M.
Let
be defined for all
in an open interval containing a. Then, we have an infinite limit
if for every
there exists
such that if
then
Let
be defined for all
in an open interval containing a. Then, we have a negative infinite limit
if for every
there exists
such that if
then
In the following exercises, write the appropriate
definition for each of the given statements.
For every
there exists a
so that if
then
For every
there exists a
so that if
then
The following graph of the function f satisfies
In the following exercises, determine a value of
that satisfies each statement.
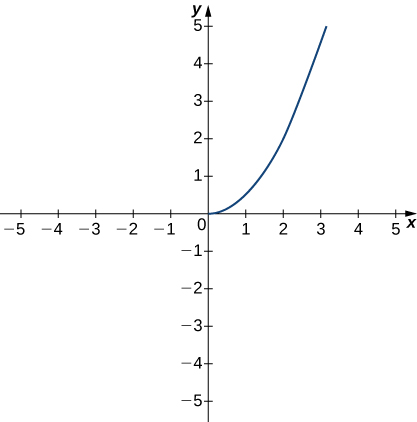
If
then
If
then
The following graph of the function f satisfies
In the following exercises, determine a value of
that satisfies each statement.
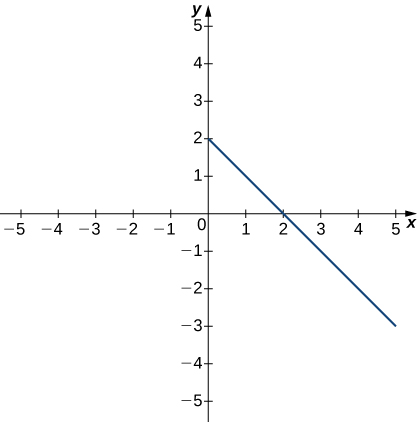
If
then
If
then
The following graph of the function f satisfies
In the following exercises, for each value of ε, find a value of
such that the precise definition of limit holds true.
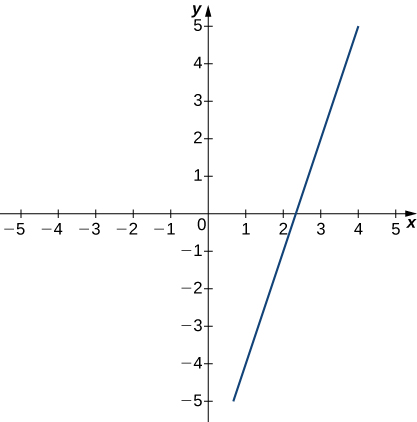
[T] In the following exercises, use a graphing calculator to find a number
such that the statements hold true.
whenever
In the following exercises, use the precise definition of limit to prove the given limits.
Let
If
then
Let
If
then
In the following exercises, use the precise definition of limit to prove the given one-sided limits.
Let
If
then
Let
If
then
In the following exercises, use the precise definition of limit to prove the given infinite limits.
Let
If
then
An engineer is using a machine to cut a flat square of Aerogel of area 144 cm2. If there is a maximum error tolerance in the area of 8 cm2, how accurately must the engineer cut on the side, assuming all sides have the same length? How do these numbers relate to
ε, a, and L?
0.033 cm,
Use the precise definition of limit to prove that the following limit does not exist:
Using precise definitions of limits, prove that
does not exist, given that
is the ceiling function. (Hint: Try any
Answers may vary.
Using precise definitions of limits, prove that
does not exist:
(Hint: Think about how you can always choose a rational number
but
Using precise definitions of limits, determine
for
(Hint: Break into two cases, x rational and x irrational.)
0
Using the function from the previous exercise, use the precise definition of limits to show that
does not exist for
For the following exercises, suppose that
and
both exist. Use the precise definition of limits to prove the following limit laws:
for any real constant c (Hint: Consider two cases:
and
(Hint:
Answers may vary.
True or False. In the following exercises, justify your answer with a proof or a counterexample.
A function has to be continuous at
if the
exists.
You can use the quotient rule to evaluate
False
If there is a vertical asymptote at
for the function
then f is undefined at the point
If
does not exist, then f is undefined at the point
False. A removable discontinuity is possible.
Using the graph, find each limit or explain why the limit does not exist.
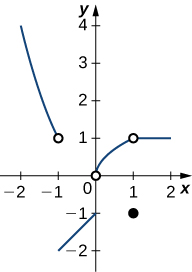
In the following exercises, evaluate the limit algebraically or explain why the limit does not exist.
5
DNE
−4;
In the following exercises, use the squeeze theorem to prove the limit.
Since
then
Since
it follows that
Determine the domain such that the function
is continuous over its domain.
In the following exercises, determine the value of c such that the function remains continuous. Draw your resulting function to ensure it is continuous.
In the following exercises, use the precise definition of limit to prove the limit.
A ball is thrown into the air and the vertical position is given by
Use the Intermediate Value Theorem to show that the ball must land on the ground sometime between 5 sec and 6 sec after the throw.
A particle moving along a line has a displacement according to the function
where x is measured in meters and t is measured in seconds. Find the average velocity over the time period
From the previous exercises, estimate the instantaneous velocity at
by checking the average velocity within
if for every
there exists a
such that if
then

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: