
In this section, we provide a formal definition of a function and examine several ways in which functions are represented—namely, through tables, formulas, and graphs. We study formal notation and terms related to functions. We also define composition of functions and symmetry properties. Most of this material will be a review for you, but it serves as a handy reference to remind you of some of the algebraic techniques useful for working with functions.
Given two sets
and
a set with elements that are ordered pairs
where
is an element of
and
is an element of
is a relation from
to
A relation from
to
defines a relationship between those two sets. A function is a special type of relation in which each element of the first set is related to exactly one element of the second set. The element of the first set is called the input; the element of the second set is called the output. Functions are used all the time in mathematics to describe relationships between two sets. For any function, when we know the input, the output is determined, so we say that the output is a function of the input. For example, the area of a square is determined by its side length, so we say that the area (the output) is a function of its side length (the input). The velocity of a ball thrown in the air can be described as a function of the amount of time the ball is in the air. The cost of mailing a package is a function of the weight of the package. Since functions have so many uses, it is important to have precise definitions and terminology to study them.
A function
consists of a set of inputs, a set of outputs, and a rule for assigning each input to exactly one output. The set of inputs is called the domain of the function. The set of outputs is called the range of the function.
For example, consider the function
where the domain is the set of all real numbers and the rule is to square the input. Then, the input
is assigned to the output
Since every nonnegative real number has a real-value square root, every nonnegative number is an element of the range of this function. Since there is no real number with a square that is negative, the negative real numbers are not elements of the range. We conclude that the range is the set of nonnegative real numbers.
For a general function
with domain
we often use
to denote the input and
to denote the output associated with
When doing so, we refer to
as the independent variable and
as the dependent variable, because it depends on
Using function notation, we write
and we read this equation as
equals
of
For the squaring function described earlier, we write
The concept of a function can be visualized using [link], [link], and [link].

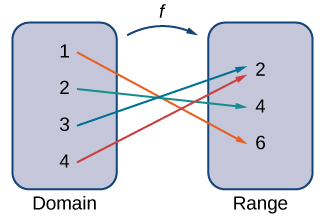
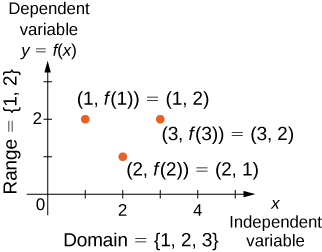
Visit this applet link to see more about graphs of functions.
We can also visualize a function by plotting points
in the coordinate plane where
The graph of a function is the set of all these points. For example, consider the function
where the domain is the set
and the rule is
In [link], we plot a graph of this function.
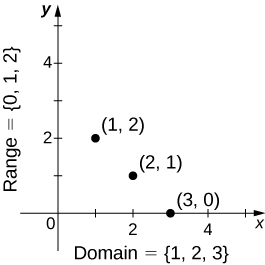
Every function has a domain. However, sometimes a function is described by an equation, as in
with no specific domain given. In this case, the domain is taken to be the set of all real numbers
for which
is a real number. For example, since any real number can be squared, if no other domain is specified, we consider the domain of
to be the set of all real numbers. On the other hand, the square root function
only gives a real output if
is nonnegative. Therefore, the domain of the function
is the set of nonnegative real numbers, sometimes called the natural domain.
For the functions
and
the domains are sets with an infinite number of elements. Clearly we cannot list all these elements. When describing a set with an infinite number of elements, it is often helpful to use set-builder or interval notation. When using set-builder notation to describe a subset of all real numbers, denoted
we write
We read this as the set of real numbers
such that
has some property. For example, if we were interested in the set of real numbers that are greater than one but less than five, we could denote this set using set-builder notation by writing
A set such as this, which contains all numbers greater than
and less than
can also be denoted using the interval notation
Therefore,
The numbers
and
are called the endpoints of this set. If we want to consider the set that includes the endpoints, we would denote this set by writing
We can use similar notation if we want to include one of the endpoints, but not the other. To denote the set of nonnegative real numbers, we would use the set-builder notation
The smallest number in this set is zero, but this set does not have a largest number. Using interval notation, we would use the symbol
which refers to positive infinity, and we would write the set as
It is important to note that
is not a real number. It is used symbolically here to indicate that this set includes all real numbers greater than or equal to zero. Similarly, if we wanted to describe the set of all nonpositive numbers, we could write
Here, the notation
refers to negative infinity, and it indicates that we are including all numbers less than or equal to zero, no matter how small. The set
refers to the set of all real numbers.
Some functions are defined using different equations for different parts of their domain. These types of functions are known as piecewise-defined functions. For example, suppose we want to define a function
with a domain that is the set of all real numbers such that
for
and
for
We denote this function by writing
When evaluating this function for an input
the equation to use depends on whether
or
For example, since
we use the fact that
for
and see that
On the other hand, for
we use the fact that
for
and see that
For the function
evaluate
Substitute the given value for x in the formula for
For
evaluate
and
and
Substitute
and
for
in the formula for
For each of the following functions, determine the i. domain and ii. range.
is a real number for any real number
the domain of
is the interval
we know
Therefore, the range must be a subset of
To show that every element in this set is in the range, we need to show that for a given
in that set, there is a real number
such that
Solving this equation for
we see that we need
such that
This equation is satisfied as long as there exists a real number
such that
Since
the square root is well-defined. We conclude that for
and therefore the range is
we need the expression
Solving this inequality, we conclude that the domain is
we note that since
Therefore, the range of
must be a subset of the set
To show that every element in this set is in the range of
we need to show that for all
in this set, there exists a real number
in the domain such that
Let
Then,
if and only if
Solving this equation for
we see that
must solve the equation
Since
such an
could exist. Squaring both sides of this equation, we have
Therefore, we need
which implies
We just need to verify that
is in the domain of
Since the domain of
consists of all real numbers greater than or equal to
and
there does exist an
in the domain of
We conclude that the range of
is
is defined when the denominator is nonzero, the domain is
we need to find the values of
such that there exists a real number
in the domain with the property that
Solving this equation for
we find that
Therefore, as long as
there exists a real number
in the domain such that
Thus, the range is
Find the domain and range for
Domain =
range =
Use
Typically, a function is represented using one or more of the following tools:
We can identify a function in each form, but we can also use them together. For instance, we can plot on a graph the values from a table or create a table from a formula.
Functions described using a table of values arise frequently in real-world applications. Consider the following simple example. We can describe temperature on a given day as a function of time of day. Suppose we record the temperature every hour for a 24-hour period starting at midnight. We let our input variable
be the time after midnight, measured in hours, and the output variable
be the temperature
hours after midnight, measured in degrees Fahrenheit. We record our data in [link].
| Hours after Midnight | Temperature | Hours after Midnight | Temperature |
|---|---|---|---|
| 0 | 58 | 12 | 84 |
| 1 | 54 | 13 | 85 |
| 2 | 53 | 14 | 85 |
| 3 | 52 | 15 | 83 |
| 4 | 52 | 16 | 82 |
| 5 | 55 | 17 | 80 |
| 6 | 60 | 18 | 77 |
| 7 | 64 | 19 | 74 |
| 8 | 72 | 20 | 69 |
| 9 | 75 | 21 | 65 |
| 10 | 78 | 22 | 60 |
| 11 | 80 | 23 | 58 |
We can see from the table that temperature is a function of time, and the temperature decreases, then increases, and then decreases again. However, we cannot get a clear picture of the behavior of the function without graphing it.
Given a function
described by a table, we can provide a visual picture of the function in the form of a graph. Graphing the temperatures listed in [link] can give us a better idea of their fluctuation throughout the day. [link] shows the plot of the temperature function.
![The graph of the data from [link] shows temperature as a function of time. An image of a graph. The y axis runs from 0 to 90 and has the label “Temperature in Fahrenheit”. The x axis runs from 0 to 24 and has the label “hours after midnight”. There are 24 points on the graph, one at each increment of 1 on the x-axis. The first point is at (0, 58) and the function decreases until x = 4, where the point is (4, 52) and is the minimum value of the function. After x=4, the function increases until x = 13, where the point is (13, 85) and is the maximum of the function along with the point (14, 85). After x = 14, the function decreases until the last point on the graph, which is (23, 58).](../resources/CNX_Calc_Figure_01_01_005.jpg)
From the points plotted on the graph in [link], we can visualize the general shape of the graph. It is often useful to connect the dots in the graph, which represent the data from the table. In this example, although we cannot make any definitive conclusion regarding what the temperature was at any time for which the temperature was not recorded, given the number of data points collected and the pattern in these points, it is reasonable to suspect that the temperatures at other times followed a similar pattern, as we can see in [link].
![Connecting the dots in [link] shows the general pattern of the data. An image of a graph. The y axis runs from 0 to 90 and has the label “Temperature in Fahrenheit”. The x axis runs from 0 to 24 and has the label “hours after midnight”. There are 24 points on the graph, one at each increment of 1 on the x-axis. The first point is at (0, 58) and the function decreases until x = 4, where the point is (4, 52) and is the minimum value of the function. After x=4, the function increases until x = 13, where the point is (13, 85) and is the maximum of the function along with the point (14, 85). After x = 14, the function decreases until the last point on the graph, which is (23, 58). A line connects all the points on the graph.](../resources/CNX_Calc_Figure_01_01_014.jpg)
Sometimes we are not given the values of a function in table form, rather we are given the values in an explicit formula. Formulas arise in many applications. For example, the area of a circle of radius
is given by the formula
When an object is thrown upward from the ground with an initial velocity
ft/s, its height above the ground from the time it is thrown until it hits the ground is given by the formula
When
dollars are invested in an account at an annual interest rate
compounded continuously, the amount of money after
years is given by the formula
Algebraic formulas are important tools to calculate function values. Often we also represent these functions visually in graph form.
Given an algebraic formula for a function
the graph of
is the set of points
where
is in the domain of
and
is in the range. To graph a function given by a formula, it is helpful to begin by using the formula to create a table of inputs and outputs. If the domain of
consists of an infinite number of values, we cannot list all of them, but because listing some of the inputs and outputs can be very useful, it is often a good way to begin.
When creating a table of inputs and outputs, we typically check to determine whether zero is an output. Those values of
where
are called the zeros of a function. For example, the zeros of
are
The zeros determine where the graph of
intersects the
-axis, which gives us more information about the shape of the graph of the function. The graph of a function may never intersect the x-axis, or it may intersect multiple (or even infinitely many) times.
Another point of interest is the
-intercept, if it exists. The
-intercept is given by
Since a function has exactly one output for each input, the graph of a function can have, at most, one
-intercept. If
is in the domain of a function
then
has exactly one
-intercept. If
is not in the domain of
then
has no
-intercept. Similarly, for any real number
if
is in the domain of
there is exactly one output
and the line
intersects the graph of
exactly once. On the other hand, if
is not in the domain of
is not defined and the line
does not intersect the graph of
This property is summarized in the vertical line test.
Given a function
every vertical line that may be drawn intersects the graph of
no more than once. If any vertical line intersects a set of points more than once, the set of points does not represent a function.
We can use this test to determine whether a set of plotted points represents the graph of a function ([link]).
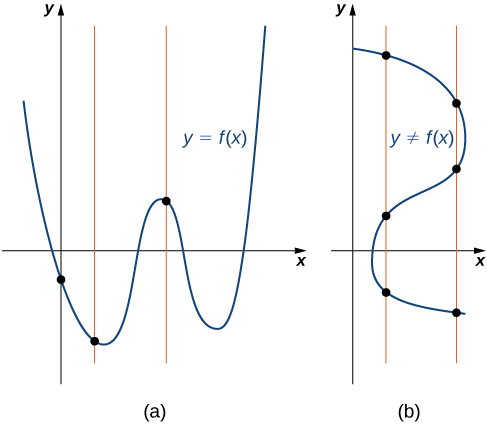
Consider the function
-intercept (if any).
We discover that
has one zero at
-intercept is given by
is a linear function of the form
that passes through the points
and
we can sketch the graph of
([link]). 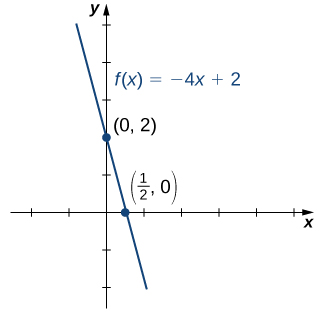
Consider the function
-intercept (if any).
This equation implies
Since
for all
this equation has no solutions, and therefore
has no zeros.
-intercept is given by
we need to choose values of
We choose values that make the square-root function easy to evaluate. |
| {: valign=”top”} |
| {: valign=”top”}{: .column-header summary=”A table with 2 rows and 3 columns. The first row is labeled “x” and has the values “-3; -2; 1”. The second row is labeled “f(x)” and has the values “1; 2; 3”.”}
Making use of the table and knowing that, since the function is a square root, the graph of
should be similar to the graph of
we sketch the graph ([link]).
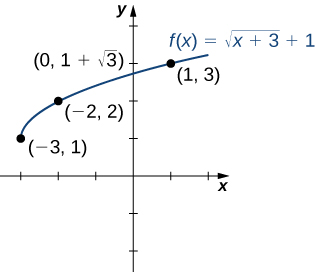
Find the zeros of
Factor the polynomial.
If a ball is dropped from a height of
ft, its height
at time
is given by the function
where
is measured in feet and
is measured in seconds. The domain is restricted to the interval
where
is the time when the ball is dropped and
is the time when the ball hits the ground.
when
Using the data from the table, determine the domain for this function. That is, find the time
when the ball hits the ground.
Since the ball hits the ground when
the domain of this function is the interval
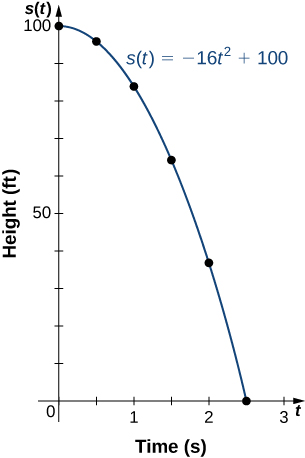
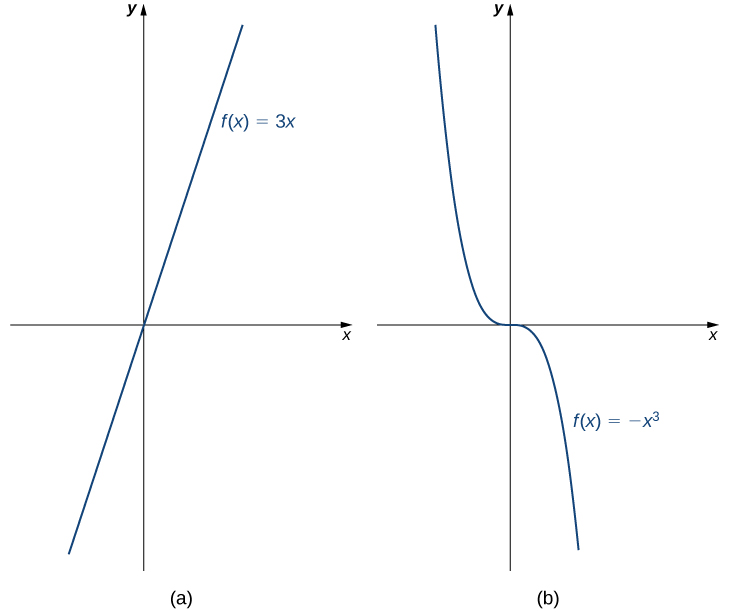
Note that for this function and the function
graphed in [link], the values of
are getting smaller as
is getting larger. A function with this property is said to be decreasing. On the other hand, for the function
graphed in [link], the values of
are getting larger as the values of
are getting larger. A function with this property is said to be increasing. It is important to note, however, that a function can be increasing on some interval or intervals and decreasing over a different interval or intervals. For example, using our temperature function in [link], we can see that the function is decreasing on the interval
increasing on the interval
and then decreasing on the interval
We make the idea of a function increasing or decreasing over a particular interval more precise in the next definition.
We say that a function
is **increasing on the interval
**{: data-type=”term”} if for all
We say
is strictly increasing on the interval
if for all
We say that a function
is **decreasing on the interval
**{: data-type=”term”} if for all
We say that a function
is strictly decreasing on the interval
if for all
For example, the function
is increasing on the interval
because
whenever
On the other hand, the function
is decreasing on the interval
because
whenever
([link]).
Now that we have reviewed the basic characteristics of functions, we can see what happens to these properties when we combine functions in different ways, using basic mathematical operations to create new functions. For example, if the cost for a company to manufacture
items is described by the function
and the revenue created by the sale of
items is described by the function
then the profit on the manufacture and sale of
items is defined as
Using the difference between two functions, we created a new function.
Alternatively, we can create a new function by composing two functions. For example, given the functions
and
the composite function
is defined such that
The composite function
is defined such that
Note that these two new functions are different from each other.
To combine functions using mathematical operators, we simply write the functions with the operator and simplify. Given two functions
and
we can define four new functions:
Given the functions
and
find each of the following functions and state its domain.
The domain of this function is the interval
The domain of this function is the interval
The domain of this function is the interval
The domain of this function is
For
and
find
and state its domain.
The domain is
The new function
is a quotient of two functions. For what values of
is the denominator zero?
When we compose functions, we take a function of a function. For example, suppose the temperature
on a given day is described as a function of time
(measured in hours after midnight) as in [link]. Suppose the cost
to heat or cool a building for 1 hour, can be described as a function of the temperature
Combining these two functions, we can describe the cost of heating or cooling a building as a function of time by evaluating
We have defined a new function, denoted
which is defined such that
for all
in the domain of
This new function is called a composite function. We note that since cost is a function of temperature and temperature is a function of time, it makes sense to define this new function
It does not make sense to consider
because temperature is not a function of cost.
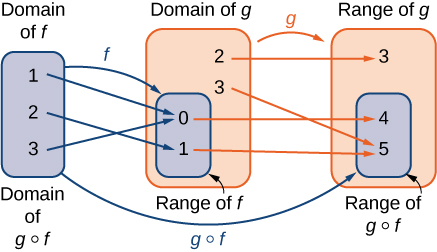
Consider the function
with domain
and range
and the function
with domain
and range
If
is a subset of
then the composite function
is the function with domain
such that
A composite function
can be viewed in two steps. First, the function
maps each input
in the domain of
to its output
in the range of
Second, since the range of
is a subset of the domain of
the output
is an element in the domain of
and therefore it is mapped to an output
in the range of
In [link], we see a visual image of a composite function.
Consider the functions
and
and state its domain and range.
and state its domain and range.
in two different ways. We could write
Alternatively, we could write
Since
for all real numbers
the domain of
is the set of all real numbers. Since
the range is, at most, the interval
To show that the range is this entire interval, we let
and solve this equation for
to show that for all
in the interval
there exists a real number
such that
Solving this equation for
we see that
which implies that
If
is in the interval
the expression under the radical is nonnegative, and therefore there exists a real number
such that
We conclude that the range of
is the interval
in two ways. First, we could write
Alternatively, we could write
The domain of
is the set of all real numbers
such that
To find the range of
we need to find all values
for which there exists a real number
such that
Solving this equation for
we see that we need
to satisfy
which simplifies to
Finally, we obtain
Since
is a real number if and only if
the range of
is the set
In [link], we can see that
This tells us, in general terms, that the order in which we compose functions matters.
Let
Let
Find
Consider the functions
and
described by [link] and [link].
| 0 | 1 | 2 | 3 | 4 |
| {: valign=”top”} |
| 0 | 4 | 2 | 4 |
| 0 |
| 4 | {: valign=”top”}{: .column-header summary=”A table with 2 rows and 8 columns. The first row is labeled “x” and has the values “-3; -2; -1; 0; 1; 2; 3; 4”. The second row is labeled “f(x)” and has the values “0; 4; 2; 4; -2; 0; -2; 4”.”}
| 0 | 2 | 4 |
| {: valign=”top”} |
| 1 | 0 | 3 | 0 | 5 | {: valign=”top”}{: .column-header summary=”A table with 2 rows and 5 columns. The first row is labeled “x” and has the values “-4; -2; 0; 2; 4”. The second row is labeled “g(x)” and has the values “1; 0; 3; 0; 5”.”}
is the set
Since the range of
is the set
the range of
is the set
is the set
Since the range of
is the set
the range of
is the set
A store is advertising a sale of
off all merchandise. Caroline has a coupon that entitles her to an additional
off any item, including sale merchandise. If Caroline decides to purchase an item with an original price of
dollars, how much will she end up paying if she applies her coupon to the sale price? Solve this problem by using a composite function.
Since the sale price is
off the original price, if an item is
dollars, its sale price is given by
Since the coupon entitles an individual to
off the price of any item, if an item is
dollars, the price, after applying the coupon, is given by
Therefore, if the price is originally
dollars, its sale price will be
and then its final price after the coupon will be
If items are on sale for
off their original price, and a customer has a coupon for an additional
off, what will be the final price for an item that is originally
dollars, after applying the coupon to the sale price?
The sale price of an item with an original price of
dollars is
The coupon price for an item that is
dollars is
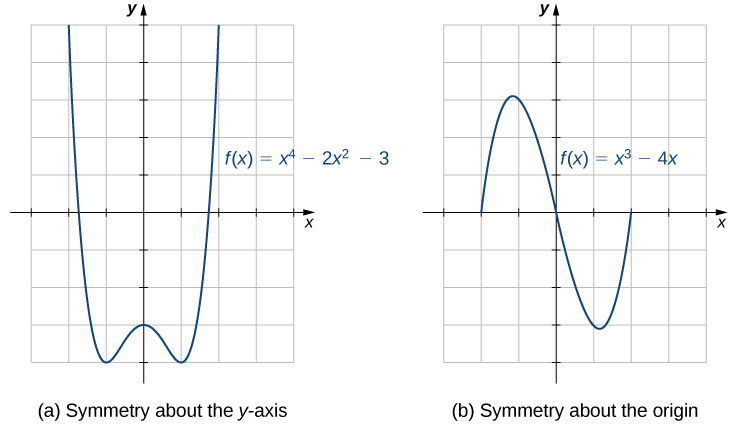
The graphs of certain functions have symmetry properties that help us understand the function and the shape of its graph. For example, consider the function
shown in [link](a). If we take the part of the curve that lies to the right of the y-axis and flip it over the y-axis, it lays exactly on top of the curve to the left of the y-axis. In this case, we say the function has symmetry about the y-axis. On the other hand, consider the function
shown in [link](b). If we take the graph and rotate it
about the origin, the new graph will look exactly the same. In this case, we say the function has symmetry about the origin.
If we are given the graph of a function, it is easy to see whether the graph has one of these symmetry properties. But without a graph, how can we determine algebraically whether a function
has symmetry? Looking at [link] again, we see that since
is symmetric about the
-axis, if the point
is on the graph, the point
is on the graph. In other words,
If a function
has this property, we say
is an even function, which has symmetry about the y-axis. For example,
is even because
In contrast, looking at [link] again, if a function
is symmetric about the origin, then whenever the point
is on the graph, the point
is also on the graph. In other words,
If
has this property, we say
is an odd function, which has symmetry about the origin. For example,
is odd because
If
for all
in the domain of
then
is an even function. An even function is symmetric about the y-axis.
If
for all
in the domain of
then
is an odd function. An odd function is symmetric about the origin.
Determine whether each of the following functions is even, odd, or neither.
To determine whether a function is even or odd, we evaluate
and compare it to f(x) and
Therefore,
is even.
Now,
Furthermore, noting that
we see that
Therefore,
is neither even nor odd.
Therefore,
is odd.
Determine whether
is even, odd, or neither.
is odd.
Compare
with
and
One symmetric function that arises frequently is the absolute value function, written as
The absolute value function is defined as
Some students describe this function by stating that it “makes everything positive.” By the definition of the absolute value function, we see that if
then
and if
then
However, for
Therefore, it is more accurate to say that for all nonzero inputs, the output is positive, but if
the output
We conclude that the range of the absolute value function is
In [link], we see that the absolute value function is symmetric about the y-axis and is therefore an even function.
| = | x | is symmetric about the y-axis.”){: #CNX_Calc_Figure_01_01_013} |
Find the domain and range of the function
Since the absolute value function is defined for all real numbers, the domain of this function is
Since
for all
the function
Therefore, the range is, at most, the set
To see that the range is, in fact, this whole set, we need to show that for
there exists a real number
such that
A real number
satisfies this equation as long as
Since
we know
and thus the right-hand side of the equation is nonnegative, so it is possible that there is a solution. Furthermore,
Therefore, we see there are two solutions:
The range of this function is
For the function
find the domain and range.
Domain =
range =
for all real numbers
the domain is considered to be the set of all real numbers
for which the function is defined.
each vertical line may intersect the graph, at most, once.
the range of
must be contained in the domain of
-axis whereas odd functions are symmetric about the origin.
For the following exercises, (a) determine the domain and the range of each relation, and (b) state whether the relation is a function.
| {: valign=”top”}|———- | −3 | 9 | 1 | 1 | {: valign=”top”}| −2 | 4 | 2 | 4 | {: valign=”top”}| −1 | 1 | 3 | 9 | {: valign=”top”}| 0 | 0 | | | {: valign=”top”}{: .unnumbered summary=”A table with 7 rows and 2 columns. The first column is labeled “x” and has the values “-3; -2; -1; 0; 1; 2; 3”. The second column is labeled “y” and the values are “9; 4; 1; 0; 1; 4; 9”.” data-label=””}
a. Domain =
range =
b. Yes, a function
| {: valign=”top”}|———- | −3 | −2 | 1 | 1 | {: valign=”top”}| −2 | −8 | 2 | 8 | {: valign=”top”}| −1 | −1 | 3 | −2 | {: valign=”top”}| 0 | 0 | | | {: valign=”top”}{: .unnumbered summary=”A table with 7 rows and 2 columns. The first column is labeled “x” and has the values “-3; -2; -1; 0; 1; 2; 3”. The second column is labeled “y” and the values are “-3; -2; -1; 0; 1; 2; 3”.” data-label=””}
| {: valign=”top”}|———- | 1 | −3 | 1 | 1 | {: valign=”top”}| 2 | −2 | 2 | 2 | {: valign=”top”}| 3 | −1 | 3 | 3 | {: valign=”top”}| 0 | 0 | | | {: valign=”top”}{: .unnumbered summary=”A table with 7 rows and 2 columns. The first column is labeled “x” and has the values “1; 2; 3; 0; 1; 2; 3”. The second column is labeled “y” and the values are “-3; -2; -1; 0; 1; 2; 3”.” data-label=””}
a. Domain =
range =
b. No, not a function
| {: valign=”top”}|———- | 1 | 1 | 5 | 1 | {: valign=”top”}| 2 | 1 | 6 | 1 | {: valign=”top”}| 3 | 1 | 7 | 1 | {: valign=”top”}| 4 | 1 | | | {: valign=”top”}{: .unnumbered summary=”A table with 7 rows and 2 columns. The first column is labeled “x” and has the values “1; 2; 3; 4; 5; 6; 7”. The second column is labeled “y” and the values are “1; 1; 1; 1; 1; 1; 1”.” data-label=””}
| {: valign=”top”}|———- | 3 | 3 | 15 | 1 | {: valign=”top”}| 5 | 2 | 21 | 2 | {: valign=”top”}| 8 | 1 | 33 | 3 | {: valign=”top”}| 10 | 0 | | | {: valign=”top”}{: .unnumbered summary=”A table with 7 rows and 2 columns. The first column is labeled “x” and has the values “3; 5; 8; 10; 15; 21; 33”. The second column is labeled “y” and the values are “3; 2; 1; 0; 1; 2; 3”.” data-label=””}
a. Domain =
range =
b. Yes, a function
| {: valign=”top”}|———- | −7 | 11 | 1 | −2 | {: valign=”top”}| −2 | 5 | 3 | 4 | {: valign=”top”}| −2 | 1 | 6 | 11 | {: valign=”top”}| 0 | −1 | | | {: valign=”top”}{: .unnumbered summary=”A table with 7 rows and 2 columns. The first column is labeled “x” and has the values “-7; -2; -2; 0; 1; 3; 6”. The second column is labeled “y” and the values are “11; 5; 1; -1; -2; 4; 11”.” data-label=””}
For the following exercises, find the values for each function, if they exist, then simplify.
a.
b.
c.
d.
e.
f.
a.
b. 3 c. 13 d.
e.
f.
a. Undefined b. 2 c.
d.
e
f.
a.
b.
c.
d.
e.
f.
a. 9 b. 9 c. 9 d. 9 e. 9 f. 9
For the following exercises, find the domain, range, and all zeros/intercepts, if any, of the functions.
no y-intercept
no x-intercept;
no intercepts
For the following exercises, set up a table to sketch the graph of each function using the following values:
| {: valign=”top”}|———- | −3 | 10 | 1 | 2 | {: valign=”top”}| −2 | 5 | 2 | 5 | {: valign=”top”}| −1 | 2 | 3 | 10 | {: valign=”top”}| 0 | 1 | | | {: valign=”top”}{: .unnumbered summary=”A table with 7 rows and 2 columns. The first column is labeled “x” and has the values “-3; -2; -1; 0; 1; 2; 3”. The second column is labeled “y” and the values are “10; 5; 2; 1; 2; 5; 10”.” data-label=””}
| {: valign=”top”}|———- | −3 | −15 | 1 | −3 | {: valign=”top”}| −2 | −12 | 2 | 0 | {: valign=”top”}| −1 | −9 | 3 | 3 | {: valign=”top”}| 0 | −6 | | | {: valign=”top”}{: .unnumbered summary=”A table with 7 rows and 2 columns. The first column is labeled “x” and has the values “-3; -2; -1; 0; 1; 2; 3”. The second column is labeled “y” and the values are “-15; -12; -9; -6; -3; 0; 3”.” data-label=””}
| {: valign=”top”} | ———- |
| −3 |
| 1 |
| {: valign=”top”} | −2 | 0 | 2 | 2 |
| {: valign=”top”} | −1 |
| 3 |
| {: valign=”top”}| 0 | 1 | | | {: valign=”top”}{: .unnumbered summary=”A table with 7 rows and 2 columns. The first column is labeled “x” and has the values “-3; -2; -1; 0; 1; 2; 3”. The second column is labeled “y” and the values are “-(1/2); 0; (1/2); 1; (3/2); 2; (5/2)”.” data-label=””}
| {: valign=”top”}|———- | −3 | 6 | 1 | 2 | {: valign=”top”}| −2 | 4 | 2 | 4 | {: valign=”top”}| −1 | 2 | 3 | 6 | {: valign=”top”}| 0 | 0 | | | {: valign=”top”}{: .unnumbered summary=”A table with 7 rows and 2 columns. The first column is labeled “x” and has the values “-3; -2; -1; 0; 1; 2; 3”. The second column is labeled “y” and the values are “6; 4; 2; 0; 2; 4; 6”.” data-label=””}
| {: valign=”top”}|———- | −3 | −9 | 1 | −1 | {: valign=”top”}| −2 | −4 | 2 | −4 | {: valign=”top”}| −1 | −1 | 3 | −9 | {: valign=”top”}| 0 | 0 | | | {: valign=”top”}{: .unnumbered summary=”A table with 7 rows and 2 columns. The first column is labeled “x” and has the values “-3; -2; -1; 0; 1; 2; 3”. The second column is labeled “y” and the values are “-9; -4; -1; 0; -1; -4; -9”.” data-label=””}
| {: valign=”top”}|———- | −3 | −27 | 1 | 1 | {: valign=”top”}| −2 | −8 | 2 | 8 | {: valign=”top”}| −1 | −1 | 3 | 27 | {: valign=”top”}| 0 | 0 | | | {: valign=”top”}{: .unnumbered summary=”A table with 7 rows and 2 columns. The first column is labeled “x” and has the values “-3; -2; -1; 0; 1; 2; 3”. The second column is labeled “y” and the values are “-27; -8; -1; 0; 1; 8; 27”.” data-label=””}
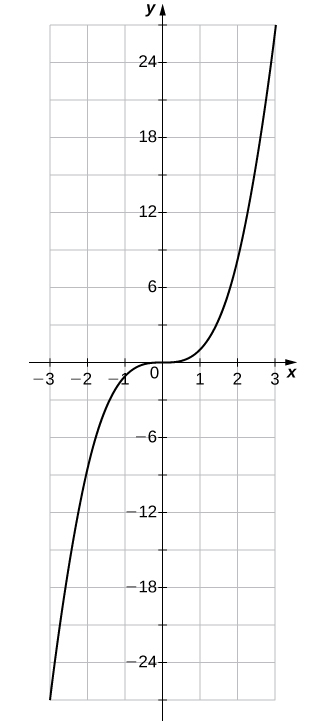
For the following exercises, use the vertical line test to determine whether each of the given graphs represents a function. Assume that a graph continues at both ends if it extends beyond the given grid. If the graph represents a function, then determine the following for each graph:
-intercept, if any (estimate where necessary)
-Intercept, if any (estimate where necessary)
Function; a. Domain: all real numbers, range:
b.
c.
d.
and
e.
and
f. Not constant g. y-axis h. Even
Function; a. Domain: all real numbers, range:
b.
c.
d.
e. None f. Not constant g. Origin h. Odd
Function; a. Domain:
range:
b.
c.
d.
e. Not decreasing f.
and
g. Origin h. Odd
Function; a. Domain:
range:
b.
c.
d. Not increasing e.
f.
g. No Symmetry h. Neither
For the following exercises, for each pair of functions, find a.
b.
c.
d.
Determine the domain of each of these new functions.
a.
all real numbers b.
all real numbers c.
all real numbers d.
a.
all real numbers b.
all real numbers c.
all real numbers d.
a.
b. 6;
c.
d.
For the following exercises, for each pair of functions, find a.
and b.
Simplify the results. Find the domain of each of the results.
a.
all real numbers b.
all real numbers
a.
all real numbers b.
all real numbers
a.
b.
The table below lists the NBA championship winners for the years 2001 to 2012.
| Year | Winner | {: valign=”top”}|———- | 2001 | LA Lakers | {: valign=”top”}| 2002 | LA Lakers | {: valign=”top”}| 2003 | San Antonio Spurs | {: valign=”top”}| 2004 | Detroit Pistons | {: valign=”top”}| 2005 | San Antonio Spurs | {: valign=”top”}| 2006 | Miami Heat | {: valign=”top”}| 2007 | San Antonio Spurs | {: valign=”top”}| 2008 | Boston Celtics | {: valign=”top”}| 2009 | LA Lakers | {: valign=”top”}| 2010 | LA Lakers | {: valign=”top”}| 2011 | Dallas Mavericks | {: valign=”top”}| 2012 | Miami Heat | {: valign=”top”}{: .unnumbered summary=”A table with 12 rows and 2 columns. The first column is labeled “year” and has the values “2001; 2002; 2003; 2004; 2005; 2006; 2007; 2008; 2009; 2010; 2011; 2012”. The second column is labeled “winner” and the values are “LA Lakers; LA Lakers; San Antonio Spurs; Detroit Pistons; San Antonio Spurs; Miami Heat; San Antonio Spurs; Boston Celtics; LA Lakers; LA Lakers; Dallas Mavericks; Miami Heat”.” data-label=””}
a. Yes, because there is only one winner for each year. b. No, because there are three teams that won more than once during the years 2001 to 2012.
[T] The area
of a square depends on the length of the side
for the area of a square.
[T] The volume of a cube depends on the length of the sides
for the area of a square.
a.
b.
a cube of side length 11.8 each has a volume of approximately 1643 cubic units.
[T] A rental car company rents cars for a flat fee of $20 and an hourly charge of $10.25. Therefore, the total cost
to rent a car is a function of the hours
the car is rented plus the flat fee.
[T] A vehicle has a 20-gal tank and gets 15 mpg. The number of miles N that can be driven depends on the amount of gas x in the tank.
a.
b. i.
therefore, the vehicle can travel 300 mi on a full tank of gas. Ii.
therefore, the vehicle can travel 225 mi on 3/4 of a tank of gas. c. Domain:
range:
d. The driver had to stop at least once, given that it takes approximately 39 gal of gas to drive a total of 578 mi.
[T] The volume V of a sphere depends on the length of its radius as
Because Earth is not a perfect sphere, we can use the mean radius when measuring from the center to its surface. The mean radius is the average distance from the physical center to the surface, based on a large number of samples. Find the volume of Earth with mean radius
m.
[T] A certain bacterium grows in culture in a circular region. The radius of the circle, measured in centimeters, is given by
where t is time measured in hours since a circle of a 1-cm radius of the bacterium was put into the culture.
a.
b. Exact:
approximately 95 cm2 c.
d. Exact:
approximately 35 cm
[T] An American tourist visits Paris and must convert U.S. dollars to Euros, which can be done using the function
where x is the number of U.S. dollars and
is the equivalent number of Euros. Since conversion rates fluctuate, when the tourist returns to the United States 2 weeks later, the conversion from Euros to U.S. dollars is
where x is the number of Euros and
is the equivalent number of U.S. dollars.
[T] The manager at a skateboard shop pays his workers a monthly salary S of $750 plus a commission of $8.50 for each skateboard they sell.
that models a worker’s monthly salary based on the number of skateboards x he or she sells.
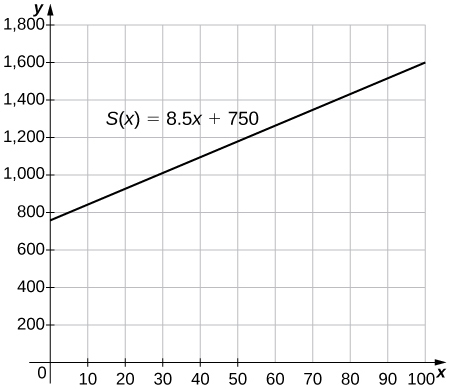
a.
b. $962.50, $1090, $1217.50 c. 77 skateboards
[T] Use a graphing calculator to graph the half-circle
Then, use the INTERCEPT feature to find the value of both the
-intercepts.
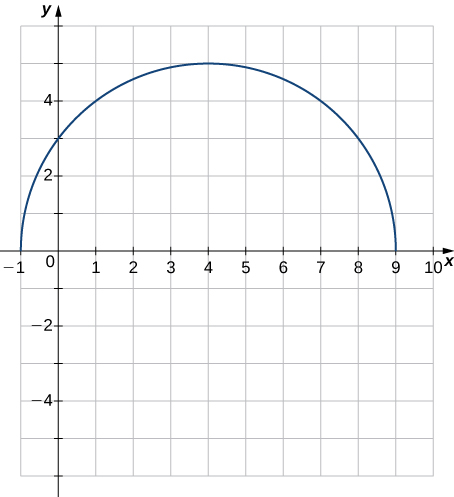
and
a new function, denoted
such that
decreasing on the interval
: a function decreasing on the interval
if, for all
if
for all
in the domain of
such that
is in the domain of
and
increasing on the interval
: a function increasing on the interval
if for all
if
for all
in the domain of
is symmetric about the origin if
is on the graph of
whenever
is on the graph
is symmetric about the
-axis if
is on the graph of
whenever
is on the graph
is a zero of a function

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: