Proofs, Identities, and Toolkit Functions

Appendix

Important Proofs and Derivations

Product Rule

\log_{a} x y = \log_{a} x + \log_{a} y

Proof:

Let $m = \log_{a} x$

and $n = \log_{a} y .$

Write in exponent form.

x = a^{m}

and $y = a^{n} .$

Multiply.

x y = a^{m} a^{n} = a^{m + n}

\begin{matrix} a^{m + n} & = & x y \\ \log_{a} (x y) & = & m + n \\ = & \log_{a} x + \log_{b} y \end{matrix}

Change of Base Rule

\begin{array}{l} \log_{a} b = \frac{\log_{c} b}{\log_{c} a} \\ \log_{a} b = \frac{1}{\log_{b} a} \end{array}

where $x$

and $y$

are positive, and $a > 0, a \neq 1.$

Proof:

Let $x = \log_{a} b .$

Write in exponent form.

a^{x} = b

Take the $\log_{c}$

of both sides.

\begin{matrix} \log_{c} a^{x} & = & \log_{c} b \\ x \log_{c} a & = & \log_{c} b \\ x & = & \frac{\log_{c} b}{\log_{c} a} \\ \log_{a} b & = & \frac{\log_{c} b}{\log_{a} b} \end{matrix}

When $c = b,$

\log_{a} b = \frac{\log_{b} b}{\log_{b} a} = \frac{1}{\log_{b} a}

Heron’s Formula

A = \sqrt{s (s - a) (s - b) (s - c)}

where $s = \frac{a + b + c}{2}$

Proof:

Let $a,$

b,

and $c$

be the sides of a triangle, and $h$

be the height.

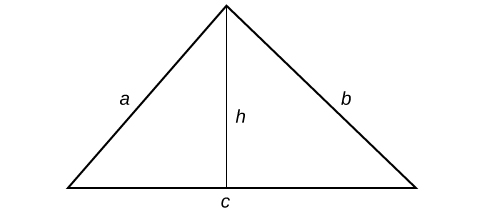
A triangle with sides labeled: a, b and c. A line runs through the center of the triangle, bisecting the top angle; this line is labeled: h.

So $s = \frac{a + b + c}{2}$

We can further name the parts of the base in each triangle established by the height such that $p + q = c .$

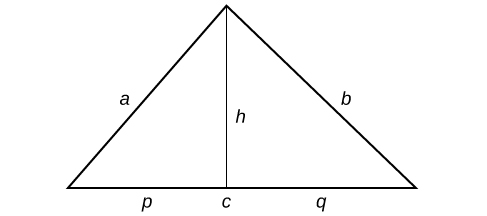
A triangle with sides labeled: a, b, and c. A line runs through the center of the triangle bisecting the angle at the top; this line is labeled: h. The two new line segments on the base of the triangle are labeled: p and q.

Using the Pythagorean Theorem, $h^{2} + p^{2} = a^{2}$

and $h^{2} + q^{2} = b^{2} .$

Since $q = c - p,$

then $q^{2} = {(c - p)}^{2} .$

Expanding, we find that $q^{2} = c^{2} - 2 c p + p^{2} .$

We can then add $h^{2}$

to each side of the equation to get $h^{2} + q^{2} = h^{2} + c^{2} - 2 c p + p^{2} .$

Substitute this result into the equation $h^{2} + q^{2} = b^{2}$

yields $b^{2} = h^{2} + c^{2} - 2 c p + p^{2} .$

Then replacing $h^{2} + p^{2}$

with $a^{2}$

gives $b^{2} = a^{2} - 2 c p + c^{2} .$

Solve for $p$

to get

p = \frac{a^{2} + b^{2} - c^{2}}{2 c}

Since $h^{2} = a^{2} - p^{2},$

we get an expression in terms of $a,$

b,

and $c .$

\begin{matrix} h^{2} & = & a^{2} - p^{2} \\ = & (a + p) (a - p) \\ = & [a + \frac{(a^{2} + c^{2} - b^{2})}{2 c}] [a - \frac{(a^{2} + c^{2} - b^{2})}{2 c}] \\ = & \frac{(2 a c + a^{2} + c^{2} - b^{2}) (2 a c - a^{2} - c^{2} + b^{2})}{4 c^{2}} \\ = & \frac{({(a + c)}^{2} - b^{2}) (b^{2} - {(a - c)}^{2})}{4 c^{2}} \\ = & \frac{(a + b + c) (a + c - b) (b + a - c) (b - a + c)}{4 c^{2}} \\ = & \frac{(a + b + c) (- a + b + c) (a - b + c) (a + b - c)}{4 c^{2}} \\ = & \frac{2 s \cdot (2 s - a) \cdot (2 s - b) (2 s - c)}{4 c^{2}} \end{matrix}

Therefore,

\begin{matrix} h^{2} & = & \frac{4 s (s - a) (s - b) (s - c)}{c^{2}} \\ h & = & \frac{2 \sqrt{s (s - a) (s - b) (s - c)}}{c} \end{matrix}

And since $A = \frac{1}{2} c h,$

then

\begin{matrix} A & = & \frac{1}{2} c \frac{2 \sqrt{s (s - a) (s - b) (s - c)}}{c} \\ = & \sqrt{s (s - a) (s - b) (s - c)} \end{matrix}

Properties of the Dot Product

u \cdot v = v \cdot u

Proof:

\begin{matrix} u \cdot v & = 〈 u_{1}, u_{2}, ... u_{n} 〉 \cdot 〈 v_{1}, v_{2}, ... v_{n} 〉 \\ = u_{1} v_{1} + u_{2} v_{2} + ... + u_{n} v_{n} \\ = v_{1} u_{1} + v_{2} u_{2} + ... + v_{n} v_{n} \\ = 〈 v_{1}, v_{2}, ... v_{n} 〉 \cdot 〈 u_{1}, u_{2}, ... u_{n} 〉 \\ = v \cdot u \end{matrix}

u \cdot (v + w) = u \cdot v + u \cdot w

Proof:

\begin{matrix} u \cdot (v + w) & = 〈 u_{1}, u_{2}, ... u_{n} 〉 \cdot (〈 v_{1}, v_{2}, ... v_{n} 〉 + 〈 w_{1}, w_{2}, ... w_{n} 〉) \\ = 〈 u_{1}, u_{2}, ... u_{n} 〉 \cdot 〈 v_{1} + w_{1}, v_{2} + w_{2}, ... v_{n} + w_{n} 〉 \\ = 〈 u_{1} (v_{1} + w_{1}), u_{2} (v_{2} + w_{2}), ... u_{n} (v_{n} + w_{n}) 〉 \\ = 〈 u_{1} v_{1} + u_{1} w_{1}, u_{2} v_{2} + u_{2} w_{2}, ... u_{n} v_{n} + u_{n} w_{n} 〉 \\ = 〈 u_{1} v_{1}, u_{2} v_{2}, ..., u_{n} v_{n} 〉 + 〈 u_{1} w_{1}, u_{2} w_{2}, ..., u_{n} w_{n} 〉 \\ = 〈 u_{1}, u_{2}, ... u_{n} 〉 \cdot 〈 v_{1}, v_{2}, ... v_{n} 〉 + 〈 u_{1}, u_{2}, ... u_{n} 〉 \cdot 〈 w_{1}, w_{2}, ... w_{n} 〉 \\ = u \cdot v + u \cdot w \end{matrix}

u \cdot u = {\| u \|}^{2}

Proof:

\begin{matrix} u \cdot u & = 〈 u_{1}, u_{2}, ... u_{n} 〉 \cdot 〈 u_{1}, u_{2}, ... u_{n} 〉 \\ = u_{1} u_{1} + u_{2} u_{2} + ... + u_{n} u_{n} \\ = u_{1}^{2} + u_{2}^{2} + ... + u_{n}^{2} \\ = \| 〈 u_{1}, u_{2}, ... u_{n} 〉 {\|}^{2} \\ = v \cdot u \end{matrix}

Standard Form of the Ellipse centered at the Origin

1 = \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}}

Derivation

An ellipse consists of all the points for which the sum of distances from two foci is constant:

\sqrt{{(x - (- c))}^{2} + {(y - 0)}^{2}} + \sqrt{{(x - c)}^{2} + {(y - 0)}^{2}} = constant

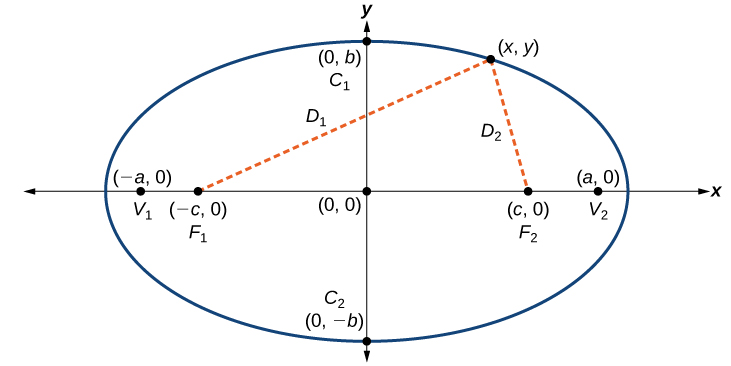
Consider a vertex.

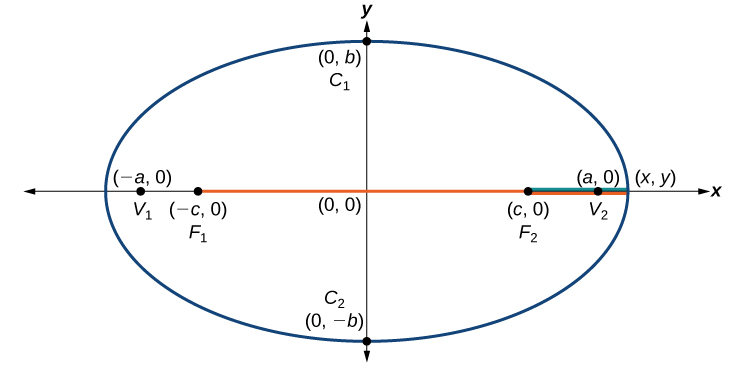
Then, $\sqrt{{(x - (- c))}^{2} + {(y - 0)}^{2}} + \sqrt{{(x - c)}^{2} + {(y - 0)}^{2}} = 2 a$

Consider a covertex.

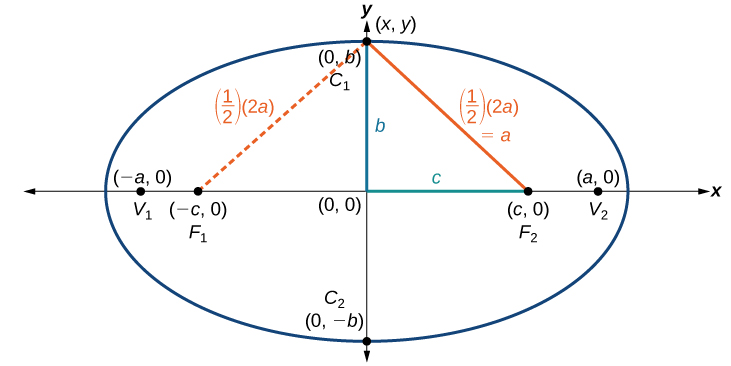
Then $b^{2} + c^{2} = a^{2} .$

\begin{matrix} \sqrt{{(x - (- c))}^{2} + {(y - 0)}^{2}} + \sqrt{{(x - c)}^{2} + {(y - 0)}^{2}} & = & 2 a \\ \sqrt{{(x + c)}^{2} + y^{2}} & = & 2 a - \sqrt{{(x - c)}^{2} + y^{2}} \\ {(x + c)}^{2} + y^{2} & = & {(2 a - \sqrt{{(x - c)}^{2} + y^{2}})}^{2} \\ x^{2} + 2 c x + c^{2} + y^{2} & = & 4 a^{2} - 4 a \sqrt{{(x - c)}^{2} + y^{2}} + {(x - c)}^{2} + y^{2} \\ x^{2} + 2 c x + c^{2} + y^{2} & = & 4 a^{2} - 4 a \sqrt{{(x - c)}^{2} + y^{2}} + x^{2} - 2 c x + y^{2} \\ 2 c x & = & 4 a^{2} - 4 a \sqrt{{(x - c)}^{2} + y^{2}} - 2 c x \\ 4 c x - 4 a^{2} & = & 4 a \sqrt{{(x - c)}^{2} + y^{2}} \\ - \frac{1}{4 a} (4 c x - 4 a^{2}) & = & \sqrt{{(x - c)}^{2} + y^{2}} \\ a - \frac{c}{a} x & = & \sqrt{{(x - c)}^{2} + y^{2}} \\ a^{2} - 2 x c + \frac{c^{2}}{a^{2}} x^{2} & = & {(x - c)}^{2} + y^{2} \\ a^{2} - 2 x c + \frac{c^{2}}{a^{2}} x^{2} & = & x^{2} - 2 x c + c^{2} + y^{2} \\ a^{2} + \frac{c^{2}}{a^{2}} x^{2} & = & x^{2} + c^{2} + y^{2} \\ a^{2} + \frac{c^{2}}{a^{2}} x^{2} & = & x^{2} + c^{2} + y^{2} \\ a^{2} - c^{2} & = & x^{2} - \frac{c^{2}}{a^{2}} x^{2} + y^{2} \\ a^{2} - c^{2} & = & x^{2} (1 - \frac{c^{2}}{a^{2}}) + y^{2} \end{matrix}

Let $1 = \frac{a^{2}}{a^{2}} .$

\begin{matrix} a^{2} - c^{2} & = & x^{2} (\frac{a^{2} - c^{2}}{a^{2}}) + y^{2} \\ 1 & = & \frac{x^{2}}{a^{2}} + \frac{y^{2}}{a^{2} - c^{2}} \end{matrix}

Because $b^{2} + c^{2} = a^{2},$

then $b^{2} = a^{2} - c^{2} .$

\begin{matrix} 1 & = & \frac{x^{2}}{a^{2}} + \frac{y^{2}}{a^{2} - c^{2}} \\ 1 & = & \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} \end{matrix}

Standard Form of the Hyperbola

1 = \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}}

Derivation

A hyperbola is the set of all points in a plane such that the absolute value of the difference of the distances between two fixed points is constant.

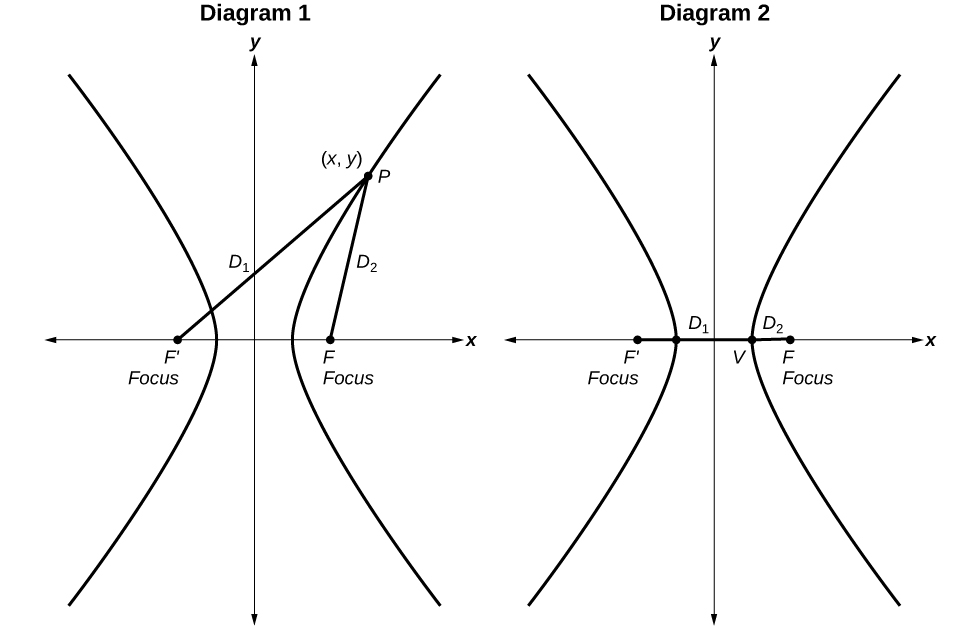
Diagram 1: The difference of the distances from Point P to the foci is constant:

\sqrt{{(x - (- c))}^{2} + {(y - 0)}^{2}} - \sqrt{{(x - c)}^{2} + {(y - 0)}^{2}} = constant

Diagram 2: When the point is a vertex, the difference is $2 a .$

\sqrt{{(x - (- c))}^{2} + {(y - 0)}^{2}} - \sqrt{{(x - c)}^{2} + {(y - 0)}^{2}} = 2 a

\begin{matrix} \sqrt{{(x - (- c))}^{2} + {(y - 0)}^{2}} - \sqrt{{(x - c)}^{2} + {(y - 0)}^{2}} & = & 2 a \\ \sqrt{{(x + c)}^{2} + y^{2}} - \sqrt{{(x - c)}^{2} + y^{2}} & = & 2 a \\ \sqrt{{(x + c)}^{2} + y^{2}} & = & 2 a + \sqrt{{(x - c)}^{2} + y^{2}} \\ {(x + c)}^{2} + y^{2} & = & (2 a + \sqrt{{(x - c)}^{2} + y^{2}}) \\ x^{2} + 2 c x + c^{2} + y^{2} & = & 4 a^{2} + 4 a \sqrt{{(x - c)}^{2}} + y^{2} \\ x^{2} + 2 c x + c^{2} + y^{2} & = & 4 a^{2} + 4 a \sqrt{{(x - c)}^{2} + y^{2}} + x^{2} - 2 c x + y^{2} \\ 2 c x & = & 4 a^{2} + 4 a \sqrt{{(x - c)}^{2} + y^{2}} - 2 c x \\ 4 c x - 4 a^{2} & = & 4 a \sqrt{{(x - c)}^{2} + y^{2}} \\ c x - a^{2} & = & a \sqrt{{(x - c)}^{2} + y^{2}} \\ {(c x - a^{2})}^{2} & = & a^{2} ({(x - c)}^{2} + y^{2}) \\ c^{2} x^{2} - 2 a^{2} c^{2} x^{2} + a^{4} & = & a^{2} x^{2} - 2 a^{2} c^{2} x^{2} + a^{2} c^{2} + a^{2} y^{2} \\ c^{2} x^{2} + a^{4} & = & a^{2} x^{2} + a^{2} c^{2} + a^{2} y^{2} \\ a^{4} - a^{2} c^{2} & = & a^{2} x^{2} - c^{2} x^{2} + a^{2} y^{2} \\ a^{2} (a^{2} - c^{2}) & = & (a^{2} - c^{2}) x^{2} + a^{2} y^{2} \\ a^{2} (a^{2} - c^{2}) & = & (c^{2} - a^{2}) x^{2} - a^{2} y^{2} \end{matrix}

Define $b$

as a positive number such that $b^{2} = c^{2} - a^{2} .$

\begin{matrix} a^{2} b^{2} & = & b^{2} x^{2} - a^{2} y^{2} \\ \frac{a^{2} b^{2}}{a^{2} b^{2}} & = & \frac{b^{2} x^{2}}{a^{2} b^{2}} - \frac{a^{2} y^{2}}{a^{2} b^{2}} \\ 1 & = & \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} \end{matrix}

Trigonometric Identities

Pythagorean Identity

\begin{array}{l} \cos^{2} t + \sin^{2} t = 1 \\ 1 + \tan^{2} t = \sec^{2} t \\ 1 + \cot^{2} t = \csc^{2} t \end{array}


Even-Odd Identities	$\begin{array}{l} \cos (- t) = c o s t \\ \sec (- t) = \sec t \\ \sin (- t) = - \sin t \\ \tan (- t) = - \tan t \\ \csc (- t) = - \csc t \\ \cot (- t) = - \cot t \end{array}$


Cofunction Identities	$\begin{array}{l} \cos t = \sin (\frac{π}{2} - t) \\ \sin t = \cos (\frac{π}{2} - t) \\ \tan t = \cot (\frac{π}{2} - t) \\ \cot t = \tan (\frac{π}{2} - t) \\ \sec t = \csc (\frac{π}{2} - t) \\ \csc t = \sec (\frac{π}{2} - t) \end{array}$


Fundamental Identities	$\begin{array}{l} \tan t = \frac{\sin t}{\cos t} \\ \sec t = \frac{1}{\cos t} \\ \csc t = \frac{1}{\sin t} \\ c o t t = \frac{1}{tan t} = \frac{cos t}{sin t} \end{array}$


Sum and Difference Identities	$\begin{array}{l} \cos (α + β) = \cos α \cos β - \sin α \sin β \\ \cos (α - β) = \cos α \cos β + \sin α \sin β \\ \sin (α + β) = \sin α \cos β + \cos α \sin β \\ \sin (α - β) = \sin α \cos β - \cos α \sin β \\ \tan (α + β) = \frac{\tan α + \tan β}{1 - \tan α \tan β} \\ \tan (α - β) = \frac{\tan α - \tan β}{1 + \tan α \tan β} \end{array}$


Double-Angle Formulas	$\begin{array}{l} \sin (2 θ) = 2 \sin θ \cos θ \\ \cos (2 θ) = \cos^{2} θ - \sin^{2} θ \\ \cos (2 θ) = 1 - 2 \sin^{2} θ \\ \cos (2 θ) = 2 \cos^{2} θ - 1 \\ \tan (2 θ) = \frac{2 \tan θ}{1 - \tan^{2} θ} \end{array}$


Half-Angle Formulas	$\begin{array}{l} \sin \frac{α}{2} = \pm \sqrt{\frac{1 - \cos α}{2}} \\ \cos \frac{α}{2} = \pm \sqrt{\frac{1 + \cos α}{2}} \\ \tan \frac{α}{2} = \pm \sqrt{\frac{1 - \cos α}{1 + \cos α}} \\ \tan \frac{α}{2} = \frac{\sin α}{1 + \cos α} \\ \tan \frac{α}{2} = \frac{1 - \cos α}{\sin α} \end{array}$


Reduction Formulas	$\begin{array}{l} \sin^{2} θ = \frac{1 - \cos (2 θ)}{2} \\ \cos^{2} θ = \frac{1 + \cos (2 θ)}{2} \\ \tan^{2} θ = \frac{1 - \cos (2 θ)}{1 + \cos (2 θ)} \end{array}$


Product-to-Sum Formulas	$\begin{array}{l} \cos α \cos β = \frac{1}{2} [\cos (α - β) + \cos (α + β)] \\ \sin α \cos β = \frac{1}{2} [\sin (α + β) + \sin (α - β)] \\ \sin α \sin β = \frac{1}{2} [\cos (α - β) - \cos (α + β)] \\ \cos α \sin β = \frac{1}{2} [\sin (α + β) - \sin (α - β)] \end{array}$


Sum-to-Product Formulas	$\begin{array}{l} \sin α + \sin β = 2 \sin (\frac{α + β}{2}) \cos (\frac{α - β}{2}) \\ \sin α - \sin β = 2 \sin (\frac{α - β}{2}) \cos (\frac{α + β}{2}) \\ \cos α - \cos β = - 2 \sin (\frac{α + β}{2}) \sin (\frac{α - β}{2}) \\ \cos α + \cos β = 2 \cos (\frac{α + β}{2}) \cos (\frac{α - β}{2}) \end{array}$


Law of Sines	$\begin{array}{l} \frac{\sin α}{a} = \frac{\sin β}{b} = \frac{\sin γ}{c} \\ \frac{a}{\sin α} = \frac{b}{\sin β} = \frac{c}{\sin γ} \end{array}$


Law of Cosines	$\begin{matrix} a^{2} = b^{2} + c^{2} - 2 b c \cos α \\ b^{2} = a^{2} + c^{2} - 2 a c \cos β \\ c^{2} = a^{2} + b^{2} - 2 a b cos γ \end{matrix}$

ToolKit Functions

Three graphs side-by-side. From left to right, graph of the identify function, square function, and square root function. All three graphs extend from -4 to 4 on each axis.

Three graphs side-by-side. From left to right, graph of the cubic function, cube root function, and reciprocal function. All three graphs extend from -4 to 4 on each axis.

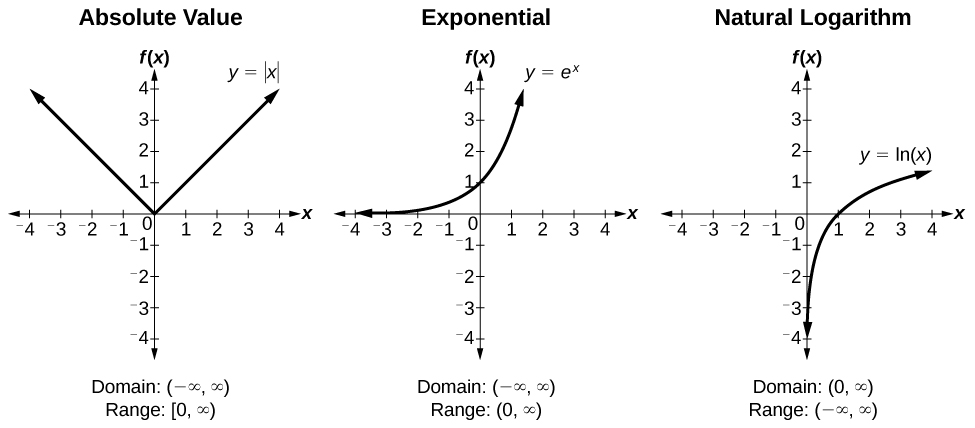
Three graphs side-by-side. From left to right, graph of the absolute value function, exponential function, and natural logarithm function. All three graphs extend from -4 to 4 on each axis.

Trigonometric Functions

Unit Circle

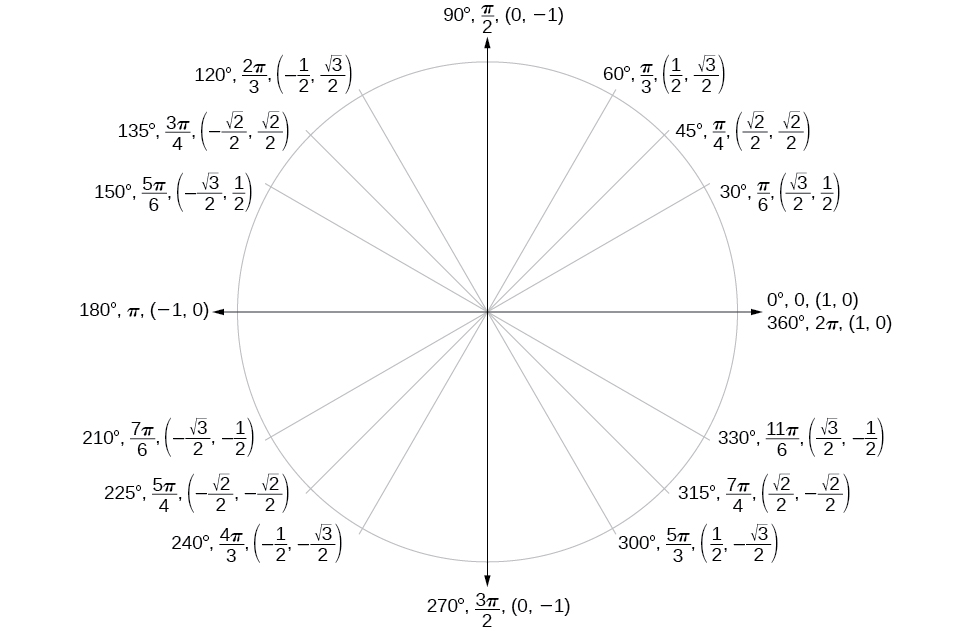
Graph of unit circle with angles in degrees, angles in radians, and points along the circle inscribed.

Angle

0

\frac{π}{6}, or 30 °

\frac{π}{4}, or 45 °

\frac{π}{3}, or 60 °

\frac{π}{2}, or 90 °


Cosine	1	$\frac{\sqrt{3}}{2}$

\frac{\sqrt{2}}{2}

\frac{1}{2}

0
Sine	0	$\frac{1}{2}$

\frac{\sqrt{2}}{2}

\frac{\sqrt{3}}{2}

1
Tangent	0	$\frac{\sqrt{3}}{3}$

1	$\sqrt{3}$

Undefined
Secant	1	$\frac{2 \sqrt{3}}{3}$

\sqrt{2}

2	Undefined
Cosecant	Undefined	2	$\sqrt{2}$

\frac{2 \sqrt{3}}{3}

1
Cotangent	Undefined	$\sqrt{3}$

1	$\frac{\sqrt{3}}{3}$

This work is licensed under a Creative Commons Attribution 4.0 International License.

You can also download for free at http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1

Attribution:

For questions regarding this license, please contact partners@openstaxcollege.org.
If you use this textbook as a bibliographic reference, then you should cite it as follows: OpenStax College, Algebra and Trigonometry. OpenStax CNX. http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1.
If you redistribute this textbook in a print format, then you must include on every physical page the following attribution: "Download for free at http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1."
If you redistribute part of this textbook, then you must retain in every digital format page view (including but not limited to EPUB, PDF, and HTML) and on every physical printed page the following attribution: "Download for free at http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1."