The Other Trigonometric Functions

In this section you will:

Find exact values of the trigonometric functions secant, cosecant, tangent, and cotangent of $\frac{π}{3}, \frac{π}{4},$
and
$\frac{π}{6} .$
Use reference angles to evaluate the trigonometric functions secant, tangent, and cotangent.
Use properties of even and odd trigonometric functions.
Recognize and use fundamental identities.
Evaluate trigonometric functions with a calculator.

A wheelchair ramp that meets the standards of the Americans with Disabilities Act must make an angle with the ground whose tangent is $\frac{1}{12}$

or less, regardless of its length. A tangent represents a ratio, so this means that for every 1 inch of rise, the ramp must have 12 inches of run. Trigonometric functions allow us to specify the shapes and proportions of objects independent of exact dimensions. We have already defined the sine and cosine functions of an angle. Though sine and cosine are the trigonometric functions most often used, there are four others. Together they make up the set of six trigonometric functions. In this section, we will investigate the remaining functions.

Finding Exact Values of the Trigonometric Functions Secant, Cosecant, Tangent, and Cotangent

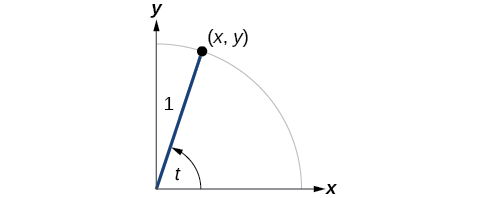
We can also define the remaining functions in terms of the unit circle with a point $(x, y)$

corresponding to an angle of $t,$

as shown in [link]. As with the sine and cosine, we can use the $(x, y)$

coordinates to find the other functions.

This image is a graph of circle with angle of t inscribed and a radius of 1. Point of (x, y) is at intersection of terminal side of angle and edge of circle.

The first function we will define is the tangent. The tangent of an angle is the ratio of the y-value to the x-value of the corresponding point on the unit circle. In [link], the tangent of angle $t$

is equal to $\frac{y}{x}, x \neq 0.$

Because the y-value is equal to the sine of $t,$

and the x-value is equal to the cosine of $t,$

the tangent of angle $t$

can also be defined as $\frac{\sin t}{\cos t}, \cos t \neq 0.$

The tangent function is abbreviated as $tan .$

The remaining three functions can all be expressed as reciprocals of functions we have already defined.

The secant function is the reciprocal of the cosine function. In [link], the secant of angle $t$
is equal to
$\frac{1}{\cos t} = \frac{1}{x}, x \neq 0.$
The secant function is abbreviated as
$sec .$
The cotangent function is the reciprocal of the tangent function. In [link], the cotangent of angle $t$
is equal to
$\frac{\cos t}{\sin t} = \frac{x}{y}, y \neq 0.$
The cotangent function is abbreviated as
$cot .$
The cosecant function is the reciprocal of the sine function. In [link], the cosecant of angle $t$
is equal to
$\frac{1}{\sin t} = \frac{1}{y}, y \neq 0.$
The cosecant function is abbreviated as
$csc .$

Tangent, Secant, Cosecant, and Cotangent Functions

If $t$

is a real number and $(x, y)$

is a point where the terminal side of an angle of $t$

radians intercepts the unit circle, then

\begin{matrix} tan t & = & \frac{y}{x}, x \neq 0 \\ sec t & = & \frac{1}{x}, x \neq 0 \\ csc t & = & \frac{1}{y}, y \neq 0 \\ cot t & = & \frac{x}{y}, y \neq 0 \end{matrix}

Finding Trigonometric Functions from a Point on the Unit Circle

The point $(- \frac{\sqrt{3}}{2}, \frac{1}{2})$

is on the unit circle, as shown in [link]. Find $\sin t, \cos t, \tan t, \sec t, \csc t,$

and $\cot t .$

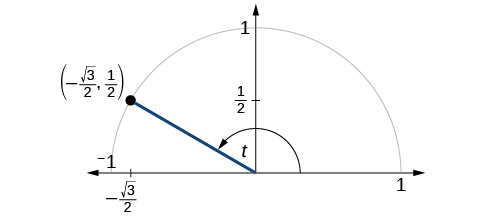
This is an image of a graph of circle with angle of t inscribed and with radius 1. Point of (negative square root of 3 over 2, 1/2) is at intersection of terminal side of angle and edge of circle.

Because we know the $(x, y)$

coordinates of the point on the unit circle indicated by angle $t,$

we can use those coordinates to find the six functions:

\begin{matrix} sin t & = y & = \frac{1}{2} \\ cos t & = x & = - \frac{\sqrt{3}}{2} \\ tan t & = \frac{y}{x} & = \frac{\frac{1}{2}}{- \frac{\sqrt{3}}{2}} & = \frac{1}{2} (- \frac{2}{\sqrt{3}}) & = - \frac{1}{\sqrt{3}} & = - \frac{\sqrt{3}}{3} \\ sec t & = \frac{1}{x} & = \frac{1}{- \frac{\sqrt{3}}{2}} & = - \frac{2}{\sqrt{3}} & = - \frac{2 \sqrt{3}}{3} \\ csc t & = \frac{1}{y} & = \frac{1}{\frac{1}{2}} & = 2 \\ cot t & = \frac{x}{y} & = \frac{- \frac{\sqrt{3}}{2}}{\frac{1}{2}} & = - \frac{\sqrt{3}}{2} (\frac{2}{1}) & = - \sqrt{3} \end{matrix}

The point $(\frac{\sqrt{2}}{2}, - \frac{\sqrt{2}}{2})$

is on the unit circle, as shown in [link]. Find $\sin t, \cos t, \tan t, \sec t, \csc t,$

and $\cot t .$

This is an image of a graph of circle with angle of t inscribed with radius 1. Point of (square root of 2 over 2, negative square root of 2 over 2) is at intersection of terminal side of angle and edge of circle.

\sin t = - \frac{\sqrt{2}}{2}, \cos t = \frac{\sqrt{2}}{2}, \tan t = - 1, s e c t = \sqrt{2}, \csc t = - \sqrt{2}, \cot t = - 1

Finding the Trigonometric Functions of an Angle

Find $\sin t, \cos t, \tan t, \sec t, \csc t,$

and $\cot t .$

when $t = \frac{π}{6} .$

We have previously used the properties of equilateral triangles to demonstrate that $\sin \frac{π}{6} = \frac{1}{2}$

and $\cos \frac{π}{6} = \frac{\sqrt{3}}{2} .$

We can use these values and the definitions of tangent, secant, cosecant, and cotangent as functions of sine and cosine to find the remaining function values.

\begin{matrix} tan \frac{π}{6} & = \frac{sin \frac{π}{6}}{cos \frac{π}{6}} \\ = \frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}} & = \frac{1}{\sqrt{3}} & = \frac{\sqrt{3}}{3} \\ sec \frac{π}{6} & = \frac{1}{cos \frac{π}{6}} \\ = \frac{1}{\frac{\sqrt{3}}{2}} & = \frac{2}{\sqrt{3}} & = \frac{2 \sqrt{3}}{3} \\ \csc \frac{π}{6} & = \frac{1}{\sin \frac{π}{6}} & = \frac{1}{\frac{1}{2}} & = 2 \\ cot \frac{π}{6} & = \frac{cos \frac{π}{6}}{sin \frac{π}{6}} \\ = \frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} & = \sqrt{3} \end{matrix}

Find $\sin t, \cos t, \tan t, \sec t, \csc t,$

and $\cot t .$

when $t = \frac{π}{3} .$

\begin{matrix} \sin \frac{π}{3} = \frac{\sqrt{3}}{2} \\ \cos \frac{π}{3} = \frac{1}{2} \\ \tan \frac{π}{3} = \sqrt{3} \\ \sec \frac{π}{3} = 2 \\ \csc \frac{π}{3} = \frac{2 \sqrt{3}}{3} \\ \cot \frac{π}{3} = \frac{\sqrt{3}}{3} \end{matrix}

Because we know the sine and cosine values for the common first-quadrant angles, we can find the other function values for those angles as well by setting $x$

equal to the cosine and $y$

equal to the sine and then using the definitions of tangent, secant, cosecant, and cotangent. The results are shown in [link].

Angle	$0$	$\frac{π}{6}, or 30°$	$\frac{π}{4}, or 45°$	$\frac{π}{3}, or 60°$	$\frac{π}{2}, or 90°$
Cosine	1	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$	0
Sine	0	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$	1
Tangent	0	$\frac{\sqrt{3}}{3}$	1	$\sqrt{3}$	Undefined
Secant	1	$\frac{2 \sqrt{3}}{3}$	$\sqrt{2}$	2	Undefined
Cosecant	Undefined	2	$\sqrt{2}$	$\frac{2 \sqrt{3}}{3}$	1
Cotangent	Undefined	$\sqrt{3}$	1	$\frac{\sqrt{3}}{3}$	0

Using Reference Angles to Evaluate Tangent, Secant, Cosecant, and Cotangent

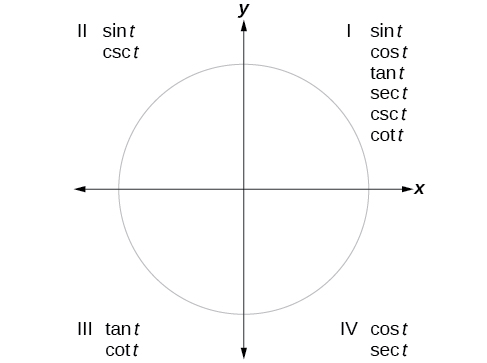
We can evaluate trigonometric functions of angles outside the first quadrant using reference angles as we have already done with the sine and cosine functions. The procedure is the same: Find the reference angle formed by the terminal side of the given angle with the horizontal axis. The trigonometric function values for the original angle will be the same as those for the reference angle, except for the positive or negative sign, which is determined by x- and y-values in the original quadrant. [link] shows which functions are positive in which quadrant.

To help remember which of the six trigonometric functions are positive in each quadrant, we can use the mnemonic phrase “A Smart Trig Class.” Each of the four words in the phrase corresponds to one of the four quadrants, starting with quadrant I and rotating counterclockwise. In quadrant I, which is “A,” **a**ll of the six trigonometric functions are positive. In quadrant II, “Smart,” only **s**ine and its reciprocal function, cosecant, are positive. In quadrant III, “Trig,” only **t**angent and its reciprocal function, cotangent, are positive. Finally, in quadrant IV, “Class,” only **c**osine and its reciprocal function, secant, are positive.

This image is a graph of circle with each quadrant labeled. Under quadrant I, labels for sin t, cos t, tan t, sec t, csc t, and cot t. Under quadrant II, labels for sin t and csc t. Under quadrant III, labels for tan t and cot t. Under quadrant IV, labels for cos t, sec t.

Given an angle not in the first quadrant, use reference angles to find all six trigonometric functions.

Measure the angle formed by the terminal side of the given angle and the horizontal axis. This is the reference angle.
Evaluate the function at the reference angle.
Observe the quadrant where the terminal side of the original angle is located. Based on the quadrant, determine whether the output is positive or negative.

Using Reference Angles to Find Trigonometric Functions

Use reference angles to find all six trigonometric functions of $- \frac{5 π}{6} .$

The angle between this angle’s terminal side and the x-axis is $\frac{π}{6},$

so that is the reference angle. Since $- \frac{5 π}{6}$

is in the third quadrant, where both $x$

and $y$

are negative, cosine, sine, secant, and cosecant will be negative, while tangent and cotangent will be positive.

\begin{matrix} cos (- \frac{5 π}{6}) & = - \frac{\sqrt{3}}{2}, sin (- \frac{5 π}{6}) & = - \frac{1}{2}, tan (- \frac{5 π}{6}) & = \frac{\sqrt{3}}{3}, \\ sec (- \frac{5 π}{6}) & = - \frac{2 \sqrt{3}}{3}, csc (- \frac{5 π}{6}) & = −2, cot (- \frac{5 π}{6}) & = \sqrt{3} \end{matrix}

Use reference angles to find all six trigonometric functions of $- \frac{7 π}{4} .$

\begin{array}{l} \sin (\frac{- 7 π}{4}) = \frac{\sqrt{2}}{2}, \cos (\frac{- 7 π}{4}) = \frac{\sqrt{2}}{2}, \tan (\frac{- 7 π}{4}) = 1, \\ \sec (\frac{- 7 π}{4}) = \sqrt{2}, \csc (\frac{- 7 π}{4}) = \sqrt{2}, \cot (\frac{- 7 π}{4}) = 1 \end{array}

Using Even and Odd Trigonometric Functions

To be able to use our six trigonometric functions freely with both positive and negative angle inputs, we should examine how each function treats a negative input. As it turns out, there is an important difference among the functions in this regard.

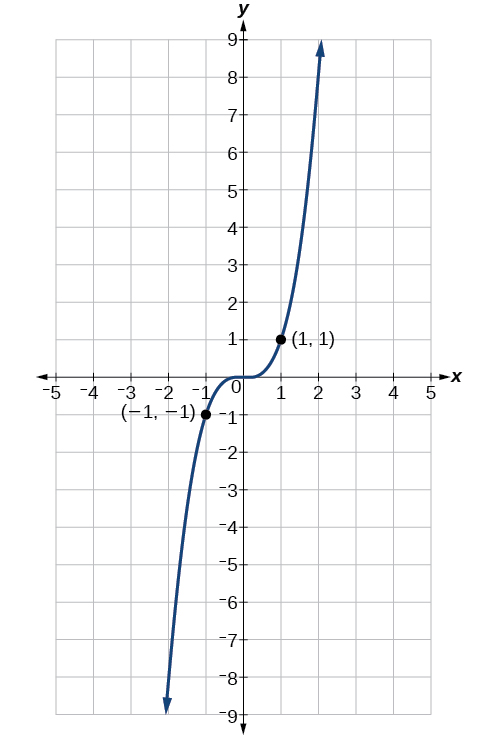
Consider the function $f (x) = x^{2},$

shown in [link]. The graph of the function is symmetrical about the y-axis. All along the curve, any two points with opposite x-values have the same function value. This matches the result of calculation: ${(4)}^{2} = {(−4)}^{2}, {(−5)}^{2} = {(5)}^{2},$

and so on. So $f (x) = x^{2}$

is an even function, a function such that two inputs that are opposites have the same output. That means $f (- x) = f (x) .$

This is an image of a graph of and upward facing parabola with points (-2, 4) and (2, 4) labeled.

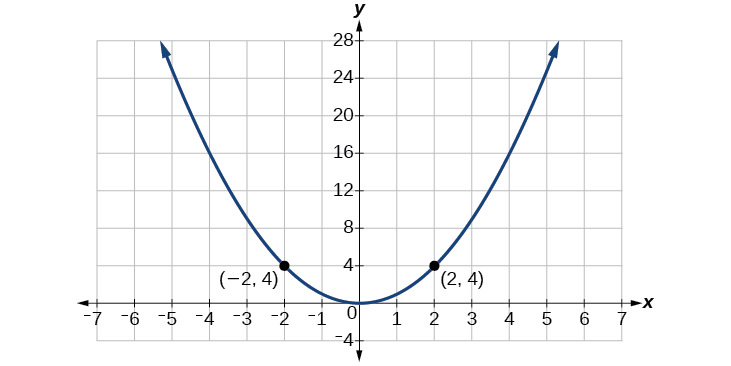
Now consider the function $f (x) = x^{3},$

shown in [link]. The graph is not symmetrical about the y-axis. All along the graph, any two points with opposite x-values also have opposite y-values. So $f (x) = x^{3}$

is an odd function, one such that two inputs that are opposites have outputs that are also opposites. That means $f (- x) = - f (x) .$

This is an image of a graph of the function f of x = x to the third power with labels for points (-1, -1) and (1, 1).

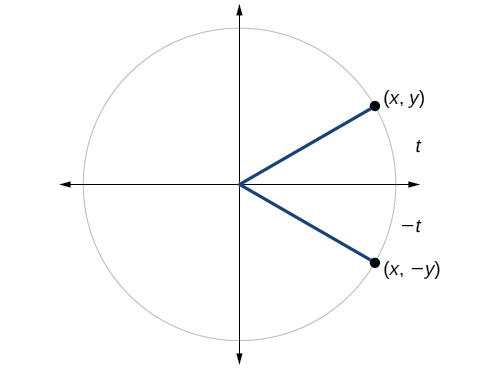
We can test whether a trigonometric function is even or odd by drawing a unit circle with a positive and a negative angle, as in [link]. The sine of the positive angle is $y .$

The sine of the negative angle is $- y .$

The sine function, then, is an odd function. We can test each of the six trigonometric functions in this fashion. The results are shown in [link].

Graph of circle with angle of t and -t inscribed. Point of (x, y) is at intersection of terminal side of angle t and edge of circle. Point of (x, -y) is at intersection of terminal side of angle -t and edge of circle.

\begin{matrix} sin t & = & y \\ sin (- t) & = & - y \\ sin t & \neq & sin (- t) \end{matrix}

\begin{matrix} cos t & = & x \\ cos (- t) & = & x \\ cos t & = & cos (- t) \end{matrix}

\begin{matrix} tan (t) & = & \frac{y}{x} \\ tan (- t) & = & - \frac{y}{x} \\ tan t & \neq & tan (- t) \end{matrix}

\begin{matrix} sec t & = & \frac{1}{x} \\ sec (- t) & = & \frac{1}{x} \\ sec t & = & sec (- t) \end{matrix}

\begin{matrix} csc t & = & \frac{1}{y} \\ csc (- t) & = & \frac{1}{- y} \\ csc t & \neq & csc (- t) \end{matrix}

\begin{matrix} cot t & = & \frac{x}{y} \\ cot (- t) & = & \frac{x}{- y} \\ cot t & \neq & cot (- t) \end{matrix}

Even and Odd Trigonometric Functions

An even function is one in which $f (- x) = f (x) .$

An odd function is one in which $f (- x) = - f (x) .$

Cosine and secant are even:

\begin{matrix} \cos (- t) & = & cos t \\ \sec (- t) & = & sec t \end{matrix}

Sine, tangent, cosecant, and cotangent are odd:

\begin{matrix} sin (- t) & = & - sin t \\ tan (- t) & = & - tan t \\ csc (- t) & = & - csc t \\ cot (- t) & = & - cot t \end{matrix}

Using Even and Odd Properties of Trigonometric Functions

If the secant of angle $t$

is 2, what is the secant of $- t ?$

Secant is an even function. The secant of an angle is the same as the secant of its opposite. So if the secant of angle $t$

is 2, the secant of $- t$

is also 2.

If the cotangent of angle $t$

is $\sqrt{3},$

what is the cotangent of $- t ?$

- \sqrt{3}

Recognizing and Using Fundamental Identities

We have explored a number of properties of trigonometric functions. Now, we can take the relationships a step further, and derive some fundamental identities. Identities are statements that are true for all values of the input on which they are defined. Usually, identities can be derived from definitions and relationships we already know. For example, the Pythagorean Identity we learned earlier was derived from the Pythagorean Theorem and the definitions of sine and cosine.

Fundamental Identities

We can derive some useful identities from the six trigonometric functions. The other four trigonometric functions can be related back to the sine and cosine functions using these basic relationships:

\tan t = \frac{\sin t}{\cos t}

\sec t = \frac{1}{\cos t}

\csc t = \frac{1}{\sin t}

cot t = \frac{1}{tan t} = \frac{cos t}{sin t}

Using Identities to Evaluate Trigonometric Functions

Given $\sin (45°) = \frac{\sqrt{2}}{2}, \cos (45°) = \frac{\sqrt{2}}{2},$
evaluate
$\tan (45°) .$
Given $\sin (\frac{5 π}{6}) = \frac{1}{2}, \cos (\frac{5 π}{6}) = - \frac{\sqrt{3}}{2},$
evaluate
$\sec (\frac{5 π}{6}) .$

Because we know the sine and cosine values for these angles, we can use identities to evaluate the other functions.

$\begin{matrix} \tan (45°) & = & \frac{\sin (45°)}{\cos (45°)} \\ = & \frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} \\ = & 1 \end{matrix}$
$\begin{matrix} \sec (\frac{5 π}{6}) & = & \frac{1}{\cos (\frac{5 π}{6})} \\ = & \frac{1}{- \frac{\sqrt{3}}{2}} \\ = & \frac{−2 \sqrt{3}}{1} \\ = & \frac{−2}{\sqrt{3}} \\ = & - \frac{2 \sqrt{3}}{3} \end{matrix}$

Evaluate $csc (\frac{7 π}{6}) .$

- 2

Using Identities to Simplify Trigonometric Expressions

Simplify $\frac{\sec t}{\tan t} .$

We can simplify this by rewriting both functions in terms of sine and cosine.

\begin{matrix} \frac{sec t}{tan t} & = & \frac{\frac{1}{cos t}}{\frac{sin t}{cos t}} \\ = & \frac{1}{cos t} \cdot \frac{cos t}{sin t} & Multiply by the reciprocal . \\ = & \frac{1}{sin t} = csc t & Simplify and use the identity . \end{matrix}

By showing that $\frac{\sec t}{\tan t}$

can be simplified to $\csc t,$

we have, in fact, established a new identity.

\frac{\sec t}{\tan t} = \csc t

Simplify $(\tan t) (\cos t) .$

\sin t

Alternate Forms of the Pythagorean Identity

We can use these fundamental identities to derive alternate forms of the Pythagorean Identity, $\cos^{2} t + \sin^{2} t = 1.$

One form is obtained by dividing both sides by $\cos^{2} t .$

\begin{matrix} \frac{\cos^{2} t}{\cos^{2} t} + \frac{\sin^{2} t}{\cos^{2} t} & = & \frac{1}{\cos^{2} t} \\ 1 + \tan^{2} t & = & \sec^{2} t \end{matrix}

The other form is obtained by dividing both sides by $\sin^{2} t .$

\begin{matrix} \frac{\cos^{2} t}{\sin^{2} t} + \frac{\sin^{2} t}{\sin^{2} t} & = & \frac{1}{\sin^{2} t} \\ \cot^{2} t + 1 & = & \csc^{2} t \end{matrix}

Alternate Forms of the Pythagorean Identity

1 + \tan^{2} t = \sec^{2} t

\cot^{2} t + 1 = \csc^{2} t

Using Identities to Relate Trigonometric Functions

If $\cos (t) = \frac{12}{13}$

and $t$

is in quadrant IV, as shown in [link], find the values of the other five trigonometric functions.

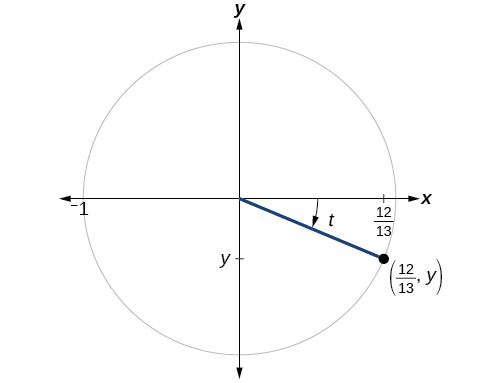
This is an image of graph of circle with angle of t inscribed. Point of (12/13, y) is at intersection of terminal side of angle and edge of circle.

We can find the sine using the Pythagorean Identity, $\cos^{2} t + \sin^{2} t = 1,$

and the remaining functions by relating them to sine and cosine.

\begin{matrix} {(\frac{12}{13})}^{2} + \sin^{2} t & = & 1 \\ \sin^{2} t & = & 1 - {(\frac{12}{13})}^{2} \\ \sin^{2} t & = & 1 - \frac{144}{169} \\ \sin^{2} t & = & \frac{25}{169} \\ sin t & = & \pm \sqrt{\frac{25}{169}} \\ sin t & = & \pm \frac{\sqrt{25}}{\sqrt{169}} \\ sin t & = & \pm \frac{5}{13} \end{matrix}

The sign of the sine depends on the y-values in the quadrant where the angle is located. Since the angle is in quadrant IV, where the y-values are negative, its sine is negative, $- \frac{5}{13} .$

The remaining functions can be calculated using identities relating them to sine and cosine.

\begin{matrix} tan t & = \frac{sin t}{cos t} & = \frac{- \frac{5}{13}}{\frac{12}{13}} & = - \frac{5}{12} \\ sec t & = \frac{1}{cos t} & = \frac{1}{\frac{12}{13}} & = \frac{13}{12} \\ csc t & = \frac{1}{sin t} & = \frac{1}{- \frac{5}{13}} & = \frac{- 13}{5} \\ cot t & = \frac{1}{tan t} & = \frac{1}{- \frac{5}{12}} & = - \frac{12}{5} \end{matrix}

If $\sec (t) = - \frac{17}{8}$

and $0 < t < π,$

find the values of the other five functions.

\begin{array}{l} \cos t = - \frac{8}{17}, \sin t = \frac{15}{17}, \tan t = - \frac{15}{8} \\ \csc t = \frac{17}{15}, \cot t = - \frac{8}{15} \end{array}

As we discussed at the beginning of the chapter, a function that repeats its values in regular intervals is known as a periodic function. The trigonometric functions are periodic. For the four trigonometric functions, sine, cosine, cosecant and secant, a revolution of one circle, or $2 π,$

will result in the same outputs for these functions. And for tangent and cotangent, only a half a revolution will result in the same outputs.

Other functions can also be periodic. For example, the lengths of months repeat every four years. If $x$

represents the length time, measured in years, and $f (x)$

represents the number of days in February, then $f (x + 4) = f (x) .$

This pattern repeats over and over through time. In other words, every four years, February is guaranteed to have the same number of days as it did 4 years earlier. The positive number 4 is the smallest positive number that satisfies this condition and is called the period. A period is the shortest interval over which a function completes one full cycle—in this example, the period is 4 and represents the time it takes for us to be certain February has the same number of days.

Period of a Function

The period $P$

of a repeating function $f$

is the number representing the interval such that $f (x + P) = f (x)$

for any value of $x .$

The period of the cosine, sine, secant, and cosecant functions is $2 π .$

The period of the tangent and cotangent functions is $π .$

Finding the Values of Trigonometric Functions

Find the values of the six trigonometric functions of angle $t$

based on [link].

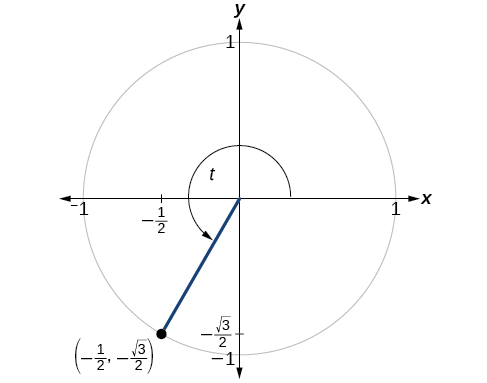
This is an image of a graph of circle with angle of t inscribed. Point of (1/2, negative square root of 3 over 2) is at intersection of terminal side of angle and edge of circle.

\begin{matrix} sin t & = y & = - \frac{\sqrt{3}}{2} \\ cos t & = x & = - \frac{1}{2} \\ tan t & = \frac{sin t}{cos t} & = \frac{- \frac{\sqrt{3}}{2}}{- \frac{1}{2}} & = \sqrt{3} \\ sec t & = \frac{1}{cos t} & = \frac{1}{- \frac{1}{2}} & = −2 \\ csc t & = \frac{1}{sin t} & = \frac{1}{- \frac{\sqrt{3}}{2}} & = - \frac{2 \sqrt{3}}{3} \\ cot t & = \frac{1}{tan t} & = \frac{1}{\sqrt{3}} & = \frac{\sqrt{3}}{3} \end{matrix}

Find the values of the six trigonometric functions of angle $t$

based on [link].

This is an image of a graph of circle with angle of t inscribed. Point of (0, -1) is at intersection of terminal side of angle and edge of circle.

\begin{array}{l} \sin t = - 1, \cos t = 0, \tan t = Undefined \\ \sec t = Undefined, \csc t = - 1, \cot t = 0 \end{array}

Finding the Value of Trigonometric Functions

If $\sin (t) = - \frac{\sqrt{3}}{2} and cos (t) = \frac{1}{2}, find sec (t), csc (t), tan (t), cot (t) .$

\begin{matrix} sec t & = \frac{1}{cos t} & = \frac{1}{\frac{1}{2}} = 2 \\ csc t & = \frac{1}{sin t} & = \frac{1}{- \frac{\sqrt{3}}{2}} - \frac{2 \sqrt{3}}{3} \\ tan t & = \frac{sin t}{cos t} & = \frac{- \frac{\sqrt{3}}{2}}{\frac{1}{2}} = - \sqrt{3} \\ cot t & = \frac{1}{tan t} & = \frac{1}{- \sqrt{3}} = - \frac{\sqrt{3}}{3} \end{matrix}

\sin (t) = \frac{\sqrt{2}}{2} and \cos (t) = \frac{\sqrt{2}}{2}, find sec (t), csc (t), tan (t), and cot (t)

\sec t = \sqrt{2}, \csc t = \sqrt{2}, \tan t = 1, \cot t = 1

Evaluating Trigonometric Functions with a Calculator

We have learned how to evaluate the six trigonometric functions for the common first-quadrant angles and to use them as reference angles for angles in other quadrants. To evaluate trigonometric functions of other angles, we use a scientific or graphing calculator or computer software. If the calculator has a degree mode and a radian mode, confirm the correct mode is chosen before making a calculation.

Evaluating a tangent function with a scientific calculator as opposed to a graphing calculator or computer algebra system is like evaluating a sine or cosine: Enter the value and press the TAN key. For the reciprocal functions, there may not be any dedicated keys that say CSC, SEC, or COT. In that case, the function must be evaluated as the reciprocal of a sine, cosine, or tangent.

If we need to work with degrees and our calculator or software does not have a degree mode, we can enter the degrees multiplied by the conversion factor $\frac{π}{180}$

to convert the degrees to radians. To find the secant of $30°,$

we could press

\begin{matrix} (for a scientific calculator): \frac{1}{30 \times \frac{π}{180}} COS \\ or \\ (for a graphing calculator): \frac{1}{\cos (\frac{30 π}{180})} \end{matrix}

Given an angle measure in radians, use a scientific calculator to find the cosecant.

If the calculator has degree mode and radian mode, set it to radian mode.
Enter: $1 /$
Enter the value of the angle inside parentheses.
Press the SIN key.
Press the = key.

Given an angle measure in radians, use a graphing utility/calculator to find the cosecant.

If the graphing utility has degree mode and radian mode, set it to radian mode.
Enter: $1 /$
Press the SIN key.
Enter the value of the angle inside parentheses.
Press the ENTER key.

Evaluating the Cosecant Using Technology

Evaluate the cosecant of $\frac{5 π}{7} .$

For a scientific calculator, enter information as follows:

\begin{matrix} 1/ (5 \times π / 7) SIN & = \\ \csc (\frac{5 π}{7}) & \approx & 1.279 \end{matrix}

Evaluate the cotangent of $- \frac{π}{8} .$

\approx - 2.414

Access these online resources for additional instruction and practice with other trigonometric functions.

Key Equations

Tangent function

\tan t = \frac{\sin t}{\cos t}


Secant function	$\sec t = \frac{1}{\cos t}$


Cosecant function	$\csc t = \frac{1}{\sin t}$


Cotangent function	$cot t = \frac{1}{tan t} = \frac{cos t}{sin t}$

Key Concepts

The tangent of an angle is the ratio of the y-value to the x-value of the corresponding point on the unit circle.
The secant, cotangent, and cosecant are all reciprocals of other functions. The secant is the reciprocal of the cosine function, the cotangent is the reciprocal of the tangent function, and the cosecant is the reciprocal of the sine function.
The six trigonometric functions can be found from a point on the unit circle. See [link].
Trigonometric functions can also be found from an angle. See [link].
Trigonometric functions of angles outside the first quadrant can be determined using reference angles. See [link].
A function is said to be even if $f (- x) = f (x)$
and odd if
$f (- x) = - f (x)$
for all x in the domain of f.
Cosine and secant are even; sine, tangent, cosecant, and cotangent are odd.
Even and odd properties can be used to evaluate trigonometric functions. See [link].
The Pythagorean Identity makes it possible to find a cosine from a sine or a sine from a cosine.
Identities can be used to evaluate trigonometric functions. See [link] and [link].
Fundamental identities such as the Pythagorean Identity can be manipulated algebraically to produce new identities. See [link].
The trigonometric functions repeat at regular intervals.
The period $P$
of a repeating function
$f$
is the smallest interval such that
$f (x + P) = f (x)$
for any value of
$x .$
The values of trigonometric functions can be found by mathematical analysis. See [link] and [link].
To evaluate trigonometric functions of other angles, we can use a calculator or computer software. See [link].

Section Exercises

Verbal

On an interval of $[0, 2 π),$

can the sine and cosine values of a radian measure ever be equal? If so, where?

Yes, when the reference angle is $\frac{π}{4}$

and the terminal side of the angle is in quadrants I and III. Thus, a $x = \frac{π}{4}, \frac{5 π}{4},$

the sine and cosine values are equal.

What would you estimate the cosine of $π$

degrees to be? Explain your reasoning.

For any angle in quadrant II, if you knew the sine of the angle, how could you determine the cosine of the angle?

Substitute the sine of the angle in for $y$

in the Pythagorean Theorem $x^{2} + y^{2} = 1.$

Solve for $x$

and take the negative solution.

Describe the secant function.

Tangent and cotangent have a period of $π .$

What does this tell us about the output of these functions?

The outputs of tangent and cotangent will repeat every $π$

units.

Algebraic

For the following exercises, find the exact value of each expression.

\tan \frac{π}{6}

\sec \frac{π}{6}

\frac{2 \sqrt{3}}{3}

\csc \frac{π}{6}

\cot \frac{π}{6}

\sqrt{3}

\tan \frac{π}{4}

\sec \frac{π}{4}

\sqrt{2}

\csc \frac{π}{4}

\cot \frac{π}{4}

\tan \frac{π}{3}

\sec \frac{π}{3}

\csc \frac{π}{3}

\cot \frac{π}{3}

\frac{\sqrt{3}}{3}

For the following exercises, use reference angles to evaluate the expression.

\tan \frac{5 π}{6}

\sec \frac{7 π}{6}

- \frac{2 \sqrt{3}}{3}

\csc \frac{11 π}{6}

\cot \frac{13 π}{6}

\sqrt{3}

\tan \frac{7 π}{4}

\sec \frac{3 π}{4}

- \sqrt{2}

\csc \frac{5 π}{4}

\cot \frac{11 π}{4}

–1

\tan \frac{8 π}{3}

\sec \frac{4 π}{3}

-2

\csc \frac{2 π}{3}

\cot \frac{5 π}{3}

- \frac{\sqrt{3}}{3}

\tan 225°

\sec 300°

\csc 150°

\cot 240°

\frac{\sqrt{3}}{3}

\tan 330°

\sec 120°

–2

\csc 210°

\cot 315°

–1

If $sin t = \frac{3}{4},$

and $t$

is in quadrant II, find $\cos t, \sec t, \csc t, \tan t,$

and $\cot t .$

If $cos t = - \frac{1}{3},$

and $t$

is in quadrant III, find $\sin t, \sec t, \csc t, \tan t,$

and $\cot t .$

\sin t = - \frac{2 \sqrt{2}}{3}, \sec t = - 3, \csc t = - \frac{3 \sqrt{2}}{4}, \tan t = 2 \sqrt{2}, \cot t = \frac{\sqrt{2}}{4}

If $\tan t = \frac{12}{5},$

and $0 \leq t < \frac{π}{2},$

find $\sin t, \cos t, \sec t, \csc t, and \cot t .$

If $\sin t = \frac{\sqrt{3}}{2}$

and $\cos t = \frac{1}{2},$

find $\sec t, \csc t, \tan t,$

and $\cot t .$

\sec t = 2,

\csc t = \frac{2 \sqrt{3}}{3},

\tan t = \sqrt{3},

\cot t = \frac{\sqrt{3}}{3}

If $\sin 40° \approx 0.643$

and $\cos 40° \approx 0.766,$

find $sec 40°, csc 40°, tan 40°,$

and $cot 40° .$

If $sin t = \frac{\sqrt{2}}{2},$

what is the $sin (- t) ?$

- \frac{\sqrt{2}}{2}

If $cos t = \frac{1}{2},$

what is the $cos (- t) ?$

If $sec t = 3.1,$

what is the $sec (- t) ?$

3.1

If $csc t = 0.34,$

what is the $csc (- t) ?$

If $tan t = −1.4,$

what is the $tan (- t) ?$

1.4

If $cot t = 9.23,$

what is the $cot (- t) ?$

Graphical

For the following exercises, use the angle in the unit circle to find the value of the each of the six trigonometric functions.

![This is an image of a graph of circle with angle of t inscribed. Point of (square root of 2 over 2, square root of 2 over 2) is at intersection of terminal side of angle and edge of circle.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_03_201.jpg)

\sin t = \frac{\sqrt{2}}{2}, \cos t = \frac{\sqrt{2}}{2}, \tan t = 1, \cot t = 1, \sec t = \sqrt{2}, \csc t = \sqrt{2}

![This is an image of a graph of circle with angle of t inscribed. Point of (square root of 3 over 2, 1/2) is at intersection of terminal side of angle and edge of circle.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_03_202.jpg)

![This is an image of a graph of circle with angle of t inscribed. Point of (-1/2, negative square root of 3 over 2) is at intersection of terminal side of angle and edge of circle.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_03_203.jpg)

\sin t = - \frac{\sqrt{3}}{2}, \cos t = - \frac{1}{2}, \tan t = \sqrt{3}, \cot t = \frac{\sqrt{3}}{3}, \sec t = - 2, \csc t = - \frac{2 \sqrt{3}}{3}

Technology

For the following exercises, use a graphing calculator to evaluate to three decimal places.

\csc \frac{5 π}{9}

\cot \frac{4 π}{7}

–0.228

\sec \frac{π}{10}

\tan \frac{5 π}{8}

–2.414

\sec \frac{3 π}{4}

\csc \frac{π}{4}

1.414

tan 98°

\cot 33°

1.540

\cot 140°

\sec 310°

1.556

Extensions

For the following exercises, use identities to evaluate the expression.

If $\tan (t) \approx 2.7,$

and $\sin (t) \approx 0.94,$

find $\cos (t) .$

If $\tan (t) \approx 1.3,$

and $\cos (t) \approx 0.61,$

find $\sin (t) .$

\sin (t) \approx 0.79

If $\csc (t) \approx 3.2,$

and $\cos (t) \approx 0.95,$

find $\tan (t) .$

If $\cot (t) \approx 0.58,$

and $\cos (t) \approx 0.5,$

find $\csc (t) .$

\csc t \approx 1.16

Determine whether the function $f (x) = 2 \sin x \cos x$

is even, odd, or neither.

Determine whether the function $f (x) = 3 \sin^{2} x \cos x + \sec x$

is even, odd, or neither.

even

Determine whether the function $f (x) = \sin x - 2 \cos^{2} x$

is even, odd, or neither.

Determine whether the function $f (x) = \csc^{2} x + \sec x$

is even, odd, or neither.

even

For the following exercises, use identities to simplify the expression.

\csc t \tan t

\frac{\sec t}{\csc t}

\frac{\sin t}{\cos t} = \tan t

Real-World Applications

The amount of sunlight in a certain city can be modeled by the function $h = 15 \cos (\frac{1}{600} d),$

where $h$

represents the hours of sunlight, and $d$

is the day of the year. Use the equation to find how many hours of sunlight there are on February 10, the 42^nd day of the year. State the period of the function.

The amount of sunlight in a certain city can be modeled by the function $h = 16 \cos (\frac{1}{500} d),$

where $h$

represents the hours of sunlight, and $d$

is the day of the year. Use the equation to find how many hours of sunlight there are on September 24, the 267th day of the year. State the period of the function.

13.77 hours, period: $1000 π$

The equation $P = 20 \sin (2 π t) + 100$

models the blood pressure, $P,$

where $t$

represents time in seconds. (a) Find the blood pressure after 15 seconds. (b) What are the maximum and minimum blood pressures?

The height of a piston, $h,$

in inches, can be modeled by the equation $y = 2 \cos x + 6,$

where $x$

represents the crank angle. Find the height of the piston when the crank angle is $55° .$

7.73 inches

The height of a piston, $h,$

in inches, can be modeled by the equation $y = 2 \cos x + 5,$

where $x$

represents the crank angle. Find the height of the piston when the crank angle is $55° .$

Chapter Review Exercises

Angles

For the following exercises, convert the angle measures to degrees.

\frac{π}{4}

45°

- \frac{5 π}{3}

For the following exercises, convert the angle measures to radians.

−210°

- \frac{7 π}{6}

180°

Find the length of an arc in a circle of radius 7 meters subtended by the central angle of $85° .$

10.385 meters

Find the area of the sector of a circle with diameter 32 feet and an angle of $\frac{3 π}{5}$

radians.

For the following exercises, find the angle between $0°$

and $360°$

that is coterminal with the given angle.

420°

60°

−80°

For the following exercises, find the angle between 0 and $2 π$

in radians that is coterminal with the given angle.

- \frac{20 π}{11}

\frac{2 π}{11}

\frac{14 π}{5}

For the following exercises, draw the angle provided in standard position on the Cartesian plane.

−210°

This is an image of a graph of a circle with a negative angle inscribed.

75°

\frac{5 π}{4}

This is an image of a graph of a circle with an angle inscribed.

- \frac{π}{3}

Find the linear speed of a point on the equator of the earth if the earth has a radius of 3,960 miles and the earth rotates on its axis every 24 hours. Express answer in miles per hour. Round to the nearest hundredth.

1036.73 miles per hour

A car wheel with a diameter of 18 inches spins at the rate of 10 revolutions per second. What is the car’s speed in miles per hour? Round to the nearest hundredth.

Right Triangle Trigonometry

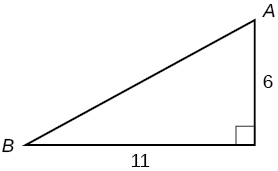
For the following exercises, use side lengths to evaluate.

\cos \frac{π}{4}

\frac{\sqrt{2}}{2}

\cot \frac{π}{3}

\tan \frac{π}{6}

\frac{\sqrt{3}}{3}

\cos (\frac{π}{2}) = \sin (\_\_\_°)

\csc (18°) = \sec (\_\_\_°)

72°

For the following exercises, use the given information to find the lengths of the other two sides of the right triangle.

\cos B = \frac{3}{5}, a = 6

\tan A = \frac{5}{9}, b = 6

a = \frac{10}{3}, c = \frac{2 \sqrt{106}}{3}

For the following exercises, use [link] to evaluate each trigonometric function.

A right triangle with side lengths of 11 and 6. Corners A and B are also labeled. The angle A is opposite the side labeled 11. The angle B is opposite the side labeled 6.

\sin A

\tan B

\frac{6}{11}

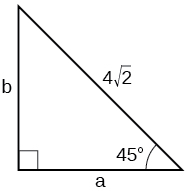
For the following exercises, solve for the unknown sides of the given triangle.

A right triangle with corners labeled A, B, and C. Hypotenuse has length of 4 times square root of 2. Other angles measure 45 degrees.

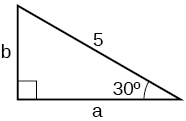
A right triangle with hypotenuse with length 5, and an angle of 30 degrees.

a = \frac{5 \sqrt{3}}{2}, b = \frac{5}{2}

A 15-ft ladder leans against a building so that the angle between the ground and the ladder is $70° .$

How high does the ladder reach up the side of the building? Find the answer to four decimal places.

The angle of elevation to the top of a building in Baltimore is found to be 4 degrees from the ground at a distance of 1 mile from the base of the building. Using this information, find the height of the building. Find the answer to four decimal places.

369.2136 ft

Unit Circle

Find the exact value of $\sin \frac{π}{3} .$

Find the exact value of $\cos \frac{π}{4} .$

\frac{\sqrt{2}}{2}

Find the exact value of $\cos π .$

State the reference angle for $300° .$

60°

State the reference angle for $\frac{3 π}{4} .$

Compute cosine of $330° .$

\frac{\sqrt{3}}{2}

Compute sine of $\frac{5 π}{4} .$

State the domain of the sine and cosine functions.

all real numbers

State the range of the sine and cosine functions.

The Other Trigonometric Functions

For the following exercises, find the exact value of the given expression.

\cos \frac{π}{6}

\frac{\sqrt{3}}{2}

\tan \frac{π}{4}

\csc \frac{π}{3}

\frac{2 \sqrt{3}}{3}

\sec \frac{π}{4}

For the following exercises, use reference angles to evaluate the given expression.

\sec \frac{11 π}{3}

\sec 315°

If $\sec (t) = −2.5,$

what is the $sec (- t) ?$

–2.5

If $tan (t) = −0.6,$

what is the $tan (- t) ?$

If $tan (t) = \frac{1}{3},$

find $tan (t - π) .$

\frac{1}{3}

If $cos (t) = \frac{\sqrt{2}}{2},$

find $sin (t + 2 π) .$

Which trigonometric functions are even?

cosine, secant

Which trigonometric functions are odd?

Chapter Practice Test

Convert $\frac{5 π}{6}$

radians to degrees.

150°

Convert $−620°$

to radians.

Find the length of a circular arc with a radius 12 centimeters subtended by the central angle of $30° .$

6.283 centimeters

Find the area of the sector with radius of 8 feet and an angle of $\frac{5 π}{4}$

radians.

Find the angle between $0°$

and $360°$

that is coterminal with $375° .$

15°

Find the angle between 0 and $2 π$

in radians that is coterminal with $- \frac{4 π}{7} .$

Draw the angle $315°$

in standard position on the Cartesian plane.

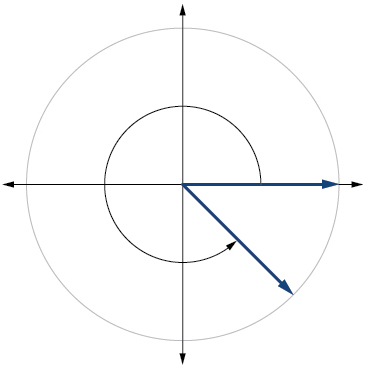
This is an image of a graph of a circle with an angle inscribed.

Draw the angle $- \frac{π}{6}$

in standard position on the Cartesian plane.

A carnival has a Ferris wheel with a diameter of 80 feet. The time for the Ferris wheel to make one revolution is 75 seconds. What is the linear speed in feet per second of a point on the Ferris wheel? What is the angular speed in radians per second?

3.351 feet per second, $\frac{2 π}{75}$

radians per second

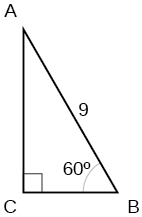
Find the missing sides of the triangle $A B C : \sin B = \frac{3}{4}, c = 12.$

Find the missing sides of the triangle.

A right triangle with hypotenuse length of 9 and angle measure of 60 degrees.

a = \frac{9}{2}, b = \frac{9 \sqrt{3}}{2}

The angle of elevation to the top of a building in Chicago is found to be 9 degrees from the ground at a distance of 2000 feet from the base of the building. Using this information, find the height of the building.

Find the exact value of $\sin \frac{π}{6} .$

\frac{1}{2}

Compute sine of $240° .$

State the domain of the sine and cosine functions.

real numbers

State the range of the sine and cosine functions.

Find the exact value of $\cot \frac{π}{4} .$

Find the exact value of $\tan \frac{π}{3} .$

Use reference angles to evaluate $\csc \frac{7 π}{4} .$

- \sqrt{2}

Use reference angles to evaluate $\tan 210° .$

If $csc t = 0.68,$

what is the $csc (- t) ?$

–0.68

If $cos t = \frac{\sqrt{3}}{2},$

find $cos (t - 2 π) .$

Find the missing angle: $\cos (\frac{π}{6}) = \sin (\_\_\_)$

\frac{π}{3}

Glossary

cosecant: the reciprocal of the sine function: on the unit circle, $csc t = \frac{1}{y}, y \neq 0$

cotangent: the reciprocal of the tangent function: on the unit circle, $cot t = \frac{x}{y}, y \neq 0$

identities: statements that are true for all values of the input on which they are defined

period

the smallest interval

P

of a repeating function

f

such that

f (x + P) = f (x)

secant: the reciprocal of the cosine function: on the unit circle, $\sec t = \frac{1}{x}, x \neq 0$

tangent: the quotient of the sine and cosine: on the unit circle, $\tan t = \frac{y}{x}, x \neq 0$

This work is licensed under a Creative Commons Attribution 4.0 International License.

You can also download for free at http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1

Attribution:

For questions regarding this license, please contact partners@openstaxcollege.org.
If you use this textbook as a bibliographic reference, then you should cite it as follows: OpenStax College, Algebra and Trigonometry. OpenStax CNX. http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1.
If you redistribute this textbook in a print format, then you must include on every physical page the following attribution: "Download for free at http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1."
If you redistribute part of this textbook, then you must retain in every digital format page view (including but not limited to EPUB, PDF, and HTML) and on every physical printed page the following attribution: "Download for free at http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1."