Unit Circle

In this section you will:

Find function values for the sine and cosine of $30° or (\frac{π}{6}), 45° or (\frac{π}{4}),$
and
$60^{\circ} or (\frac{π}{3}) .$
Identify the domain and range of sine and cosine functions.
Find reference angles.
Use reference angles to evaluate trigonometric functions.

Photo of a ferris wheel.

Looking for a thrill? Then consider a ride on the Singapore Flyer, the world’s tallest Ferris wheel. Located in Singapore, the Ferris wheel soars to a height of 541 feet—a little more than a tenth of a mile! Described as an observation wheel, riders enjoy spectacular views as they travel from the ground to the peak and down again in a repeating pattern. In this section, we will examine this type of revolving motion around a circle. To do so, we need to define the type of circle first, and then place that circle on a coordinate system. Then we can discuss circular motion in terms of the coordinate pairs.

Finding Trigonometric Functions Using the Unit Circle

We have already defined the trigonometric functions in terms of right triangles. In this section, we will redefine them in terms of the unit circle. Recall that a unit circle is a circle centered at the origin with radius 1, as shown in [link]. The angle (in radians) that $t$

intercepts forms an arc of length $s .$

Using the formula $s = r t,$

and knowing that $r = 1,$

we see that for a unit circle, $s = t .$

The x- and y-axes divide the coordinate plane into four quarters called quadrants. We label these quadrants to mimic the direction a positive angle would sweep. The four quadrants are labeled I, II, III, and IV.

For any angle $t,$

we can label the intersection of the terminal side and the unit circle as by its coordinates, $(x, y) .$

The coordinates $x$

and $y$

will be the outputs of the trigonometric functions $f (t) = \cos t$

and $f (t) = \sin t,$

respectively. This means $x = cos t$

and $y = sin t .$

Graph of a circle with angle t, radius of 1, and an arc created by the angle with length s. The terminal side of the angle intersects the circle at the point (x,y).

Unit Circle

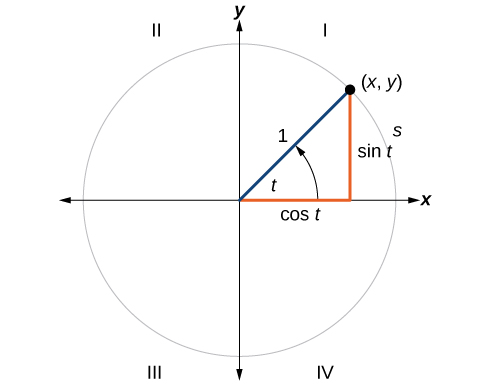
A unit circle has a center at $(0, 0)$

and radius $1.$

In a unit circle, the length of the intercepted arc is equal to the radian measure of the central angle $t .$

Let $(x, y)$

be the endpoint on the unit circle of an arc of arc length $s .$

The $(x, y)$

coordinates of this point can be described as functions of the angle.

Defining Sine and Cosine Functions from the Unit Circle

The sine function relates a real number $t$

to the y-coordinate of the point where the corresponding angle intercepts the unit circle. More precisely, the sine of an angle $t$

equals the y-value of the endpoint on the unit circle of an arc of length $t .$

In [link], the sine is equal to $y .$

Like all functions, the sine function has an input and an output. Its input is the measure of the angle; its output is the y-coordinate of the corresponding point on the unit circle.

The cosine function of an angle $t$

equals the x-value of the endpoint on the unit circle of an arc of length $t .$

In [link], the cosine is equal to $x .$

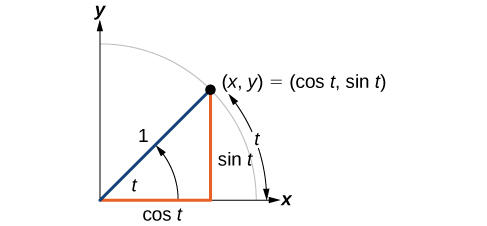
Illustration of an angle t, with terminal side length equal to 1, and an arc created by angle with length t. The terminal side of the angle intersects the circle at the point (x,y), which is equivalent to (cos t, sin t).

Because it is understood that sine and cosine are functions, we do not always need to write them with parentheses: $\sin t$

is the same as $\sin (t)$

and $\cos t$

is the same as $\cos (t) .$

Likewise, $\cos^{2} t$

is a commonly used shorthand notation for ${(\cos (t))}^{2} .$

Be aware that many calculators and computers do not recognize the shorthand notation. When in doubt, use the extra parentheses when entering calculations into a calculator or computer.

Sine and Cosine Functions

If $t$

is a real number and a point $(x, y)$

on the unit circle corresponds to a central angle $t,$

then

\cos t = x

\sin t = y

*Given a point *P $(x, y)$

on the unit circle corresponding to an angle of $t,$

find the sine and cosine.**

The sine of $t$
is equal to the y-coordinate of point
$P : sin t = y .$
The cosine of $t$
is equal to the x-coordinate of point
$P : cos t = x .$

Finding Function Values for Sine and Cosine

Point $P$

is a point on the unit circle corresponding to an angle of $t,$

as shown in [link]. Find $\cos (t)$

and $sin (t) .$

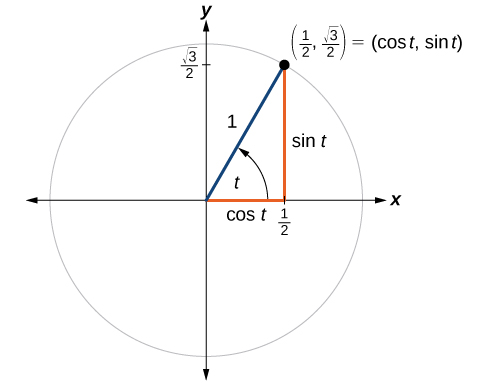
Graph of a circle with angle t, radius of 1, and a terminal side that intersects the circle at the point (1/2, square root of 3 over 2).

We know that $\cos t$

is the x-coordinate of the corresponding point on the unit circle and $\sin t$

is the y-coordinate of the corresponding point on the unit circle. So:

\begin{matrix} x & = \cos t & = \frac{1}{2} \\ y & = \sin t & = \frac{\sqrt{3}}{2} \end{matrix}

A certain angle $t$

corresponds to a point on the unit circle at $(- \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2})$

as shown in [link]. Find $\cos t$

and $\sin t .$

Graph of a circle with angle t, radius of 1, and a terminal side that intersects the circle at the point (negative square root of 2 over 2, square root of 2 over 2).

\cos (t) = - \frac{\sqrt{2}}{2}, \sin (t) = \frac{\sqrt{2}}{2}

Finding Sines and Cosines of Angles on an Axis

For quadrantral angles, the corresponding point on the unit circle falls on the x- or y-axis. In that case, we can easily calculate cosine and sine from the values of $x$

and $y .$

Calculating Sines and Cosines along an Axis

Find $cos (90°)$

and $sin (90°) .$

Moving $90°$

counterclockwise around the unit circle from the positive x-axis brings us to the top of the circle, where the $(x, y)$

coordinates are $(0, 1),$

as shown in [link].

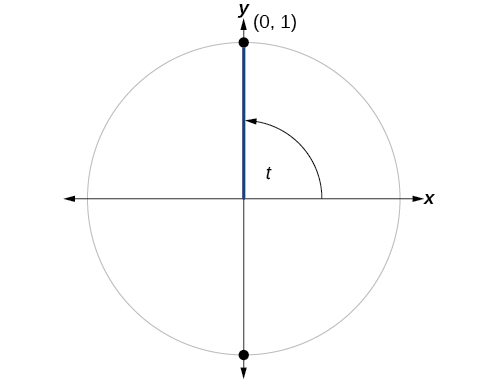
Graph of a circle with angle t, radius of 1, and a terminal side that intersects the circle at the point (0,1).

We can then use our definitions of cosine and sine.

\begin{matrix} x & = cos t & = \cos (90°) & = 0 \\ y & = sin t & = \sin (90°) & = 1 \end{matrix}

The cosine of $90°$

is 0; the sine of $90°$

is 1.

Find cosine and sine of the angle $π .$

\cos (π) = - 1, \sin (π) = 0

The Pythagorean Identity

Now that we can define sine and cosine, we will learn how they relate to each other and the unit circle. Recall that the equation for the unit circle is $x^{2} + y^{2} = 1.$

Because $x = \cos t$

and $y = \sin t,$

we can substitute for $x$

and $y$

to get $\cos^{2} t + \sin^{2} t = 1.$

This equation, $\cos^{2} t + \sin^{2} t = 1,$

is known as the Pythagorean Identity. See [link].

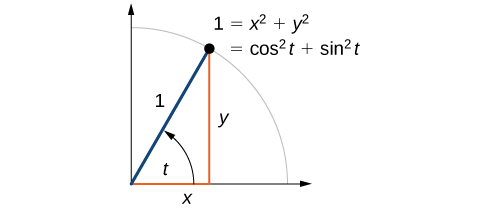
Graph of an angle t, with a point (x,y) on the unit circle. And equation showing the equivalence of 1, x^2 + y^2, and cos^2 t + sin^2 t.

We can use the Pythagorean Identity to find the cosine of an angle if we know the sine, or vice versa. However, because the equation yields two solutions, we need additional knowledge of the angle to choose the solution with the correct sign. If we know the quadrant where the angle is, we can easily choose the correct solution.

Pythagorean Identity

The Pythagorean Identity states that, for any real number $t,$

\cos^{2} t + \sin^{2} t = 1

Given the sine of some angle

</math>and its quadrant location, find the cosine of

</math> </strong>

Substitute the known value of $\sin t$
into the Pythagorean Identity.
Solve for $\cos t .$
Choose the solution with the appropriate sign for the x-values in the quadrant where $t$
is located.

Finding a Cosine from a Sine or a Sine from a Cosine

If $\sin (t) = \frac{3}{7}$

and $t$

is in the second quadrant, find $\cos (t) .$

If we drop a vertical line from the point on the unit circle corresponding to $t,$

we create a right triangle, from which we can see that the Pythagorean Identity is simply one case of the Pythagorean Theorem. See [link].

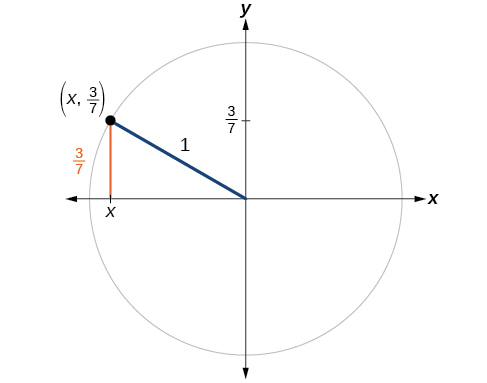
Graph of a unit circle with an angle that intersects the circle at a point with the y-coordinate equal to 3/7.

Substituting the known value for sine into the Pythagorean Identity,

\begin{matrix} {cos}^{2} (t) + \sin^{2} (t) & = & 1 \\ {cos}^{2} (t) + \frac{9}{49} & = & 1 \\ {cos}^{2} (t) & = & \frac{40}{49} \\ cos (t) & = & \pm \sqrt{\frac{40}{49}} = \pm \frac{\sqrt{40}}{7} = \pm \frac{2 \sqrt{10}}{7} \end{matrix}

Because the angle is in the second quadrant, we know the x-value is a negative real number, so the cosine is also negative.

cos (t) = - \frac{2 \sqrt{10}}{7}

If $\cos (t) = \frac{24}{25}$

and $t$

is in the fourth quadrant, find $sin (t) .$

\sin (t) = - \frac{7}{25}

Finding Sines and Cosines of Special Angles

We have already learned some properties of the special angles, such as the conversion from radians to degrees, and we found their sines and cosines using right triangles. We can also calculate sines and cosines of the special angles using the Pythagorean Identity.

Finding Sines and Cosines of $45°$

Angles

First, we will look at angles of $45°$

or $\frac{π}{4},$

as shown in [link]. A $45° - 45° - 90°$

triangle is an isosceles triangle, so the x- and y-coordinates of the corresponding point on the circle are the same. Because the x- and y-values are the same, the sine and cosine values will also be equal.

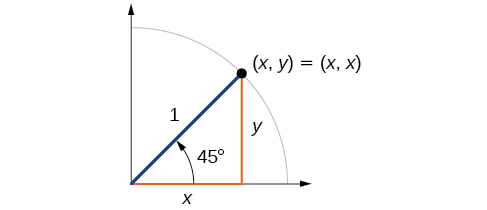
Graph of 45 degree angle inscribed within a circle with radius of 1. Equivalence between point (x,y) and (x,x) shown.

At $t = \frac{π}{4},$

which is 45 degrees, the radius of the unit circle bisects the first quadrantal angle. This means the radius lies along the line $y = x .$

A unit circle has a radius equal to 1 so the right triangle formed below the line $y = x$

has sides $x$

and $y (y = x),$

and radius = 1. See [link].

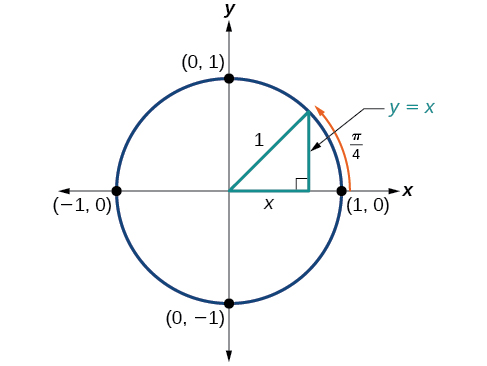
Graph of circle with pi/4 angle inscribed and a radius of 1.

From the Pythagorean Theorem we get

x^{2} + y^{2} = 1

We can then substitute $y = x .$

x^{2} + x^{2} = 1

Next we combine like terms.

2 x^{2} = 1

And solving for $x,$

we get

\begin{matrix} x^{2} & = & \frac{1}{2} \\ x & = & \pm \frac{1}{\sqrt{2}} \end{matrix}

In quadrant I, $x = \frac{1}{\sqrt{2}} .$

At $t = \frac{π}{4}$

or 45 degrees,

\begin{matrix} (x, y) & = & (x, x) = (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}) \\ x & = & \frac{1}{\sqrt{2}}, y = \frac{1}{\sqrt{2}} \\ cos t & = & \frac{1}{\sqrt{2}}, sin t = \frac{1}{\sqrt{2}} \end{matrix}

If we then rationalize the denominators, we get

\begin{matrix} cos t & = & \frac{1}{\sqrt{2}} \frac{\sqrt{2}}{\sqrt{2}} \\ = & \frac{\sqrt{2}}{2} \\ sin t & = & \frac{1}{\sqrt{2}} \frac{\sqrt{2}}{\sqrt{2}} \\ = & \frac{\sqrt{2}}{2} \end{matrix}

Therefore, the $(x, y)$

coordinates of a point on a circle of radius $1$

at an angle of $45°$

are $(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}) .$

Finding Sines and Cosines of $30°$

and $60°$

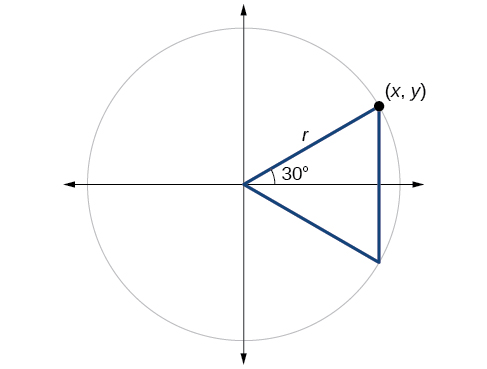
Angles

Next, we will find the cosine and sine at an angle of $30°,$

or $\frac{π}{6} .$

First, we will draw a triangle inside a circle with one side at an angle of $30°,$

and another at an angle of $−30°,$

as shown in [link]. If the resulting two right triangles are combined into one large triangle, notice that all three angles of this larger triangle will be $60°,$

as shown in [link].

Graph of a circle with 30-degree angle and negative 30-degree angle inscribed to form a triangle.

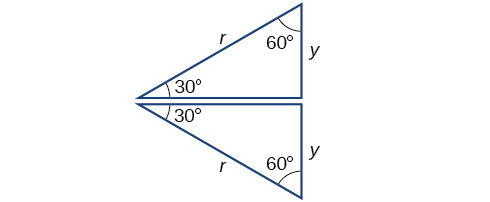
Image of two 30/60/90 triangles back to back. Label for hypotenuse r and side y.

Because all the angles are equal, the sides are also equal. The vertical line has length $2 y,$

and since the sides are all equal, we can also conclude that $r = 2 y$

or $y = \frac{1}{2} r .$

Since $\sin t = y,$

\sin (\frac{π}{6}) = \frac{1}{2} r

And since $r = 1$

in our unit circle,

\begin{matrix} \sin (\frac{π}{6}) & = & \frac{1}{2} (1) \\ = & \frac{1}{2} \end{matrix}

Using the Pythagorean Identity, we can find the cosine value.

\begin{matrix} \cos^{2} (\frac{π}{6}) + \sin^{2} (\frac{π}{6}) & = & 1 \\ \cos^{2} (\frac{π}{6}) + {(\frac{1}{2})}^{2} & = & 1 \\ \cos^{2} (\frac{π}{6}) & = & \frac{3}{4} & Use the square root property . \\ \cos (\frac{π}{6}) & = & \frac{\pm \sqrt{3}}{\pm \sqrt{4}} = \frac{\sqrt{3}}{2} & Since y is positive, choose the positive root . \end{matrix}

The $(x, y)$

coordinates for the point on a circle of radius $1$

at an angle of $30°$

are $(\frac{\sqrt{3}}{2}, \frac{1}{2}) .$

At $t = \frac{π}{3} (60°),$

the radius of the unit circle, 1, serves as the hypotenuse of a 30-60-90 degree right triangle, $B A D,$

as shown in [link]. Angle $A$

has measure $60° .$

At point $B,$

we draw an angle $A B C$

with measure of $60° .$

We know the angles in a triangle sum to $180°,$

so the measure of angle $C$

is also $60° .$

Now we have an equilateral triangle. Because each side of the equilateral triangle $A B C$

is the same length, and we know one side is the radius of the unit circle, all sides must be of length 1.

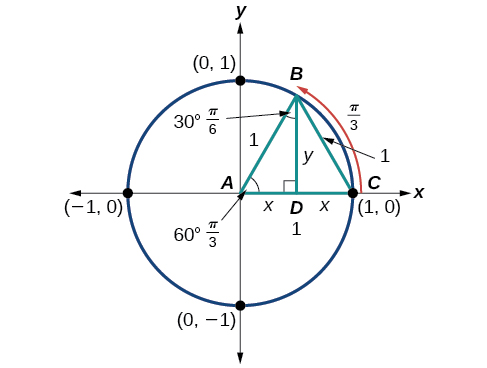
Graph of circle with an isosceles triangle inscribed that has been divided in half. The resulting triangle has a radius of 1 and a height of y. The two bases for the triangles each have a length of x.

The measure of angle $A B D$

is 30°. Angle $A B C$

is double angle $A B D,$

so its measure is 60°. $B D$

is the perpendicular bisector of $A C,$

so it cuts $A C$

in half. This means that $A D$

is $\frac{1}{2}$

the radius, or $\frac{1}{2} .$

Notice that $A D$

is the x-coordinate of point $B,$

which is at the intersection of the 60° angle and the unit circle. This gives us a triangle $B A D$

with hypotenuse of 1 and side $x$

of length $\frac{1}{2} .$

From the Pythagorean Theorem, we get

x^{2} + y^{2} = 1

Substituting $x = \frac{1}{2},$

we get

{(\frac{1}{2})}^{2} + y^{2} = 1

Solving for $y,$

we get

\begin{matrix} \frac{1}{4} + y^{2} & = & 1 \\ y^{2} & = & 1 - \frac{1}{4} \\ y^{2} & = & \frac{3}{4} \\ y & = & \pm \frac{\sqrt{3}}{2} \end{matrix}

Since $t = \frac{π}{3}$

has the terminal side in quadrant I where the y-coordinate is positive, we choose $y = \frac{\sqrt{3}}{2},$

the positive value.

At $t = \frac{π}{3}$

(60°), the $(x, y)$

coordinates for the point on a circle of radius $1$

at an angle of $60°$

are $(\frac{1}{2}, \frac{\sqrt{3}}{2}),$

so we can find the sine and cosine.

\begin{matrix} (x, y) & = & (\frac{1}{2}, \frac{\sqrt{3}}{2}) \\ x & = & \frac{1}{2}, y = \frac{\sqrt{3}}{2} \\ cos t & = & \frac{1}{2}, sin t = \frac{\sqrt{3}}{2} \end{matrix}

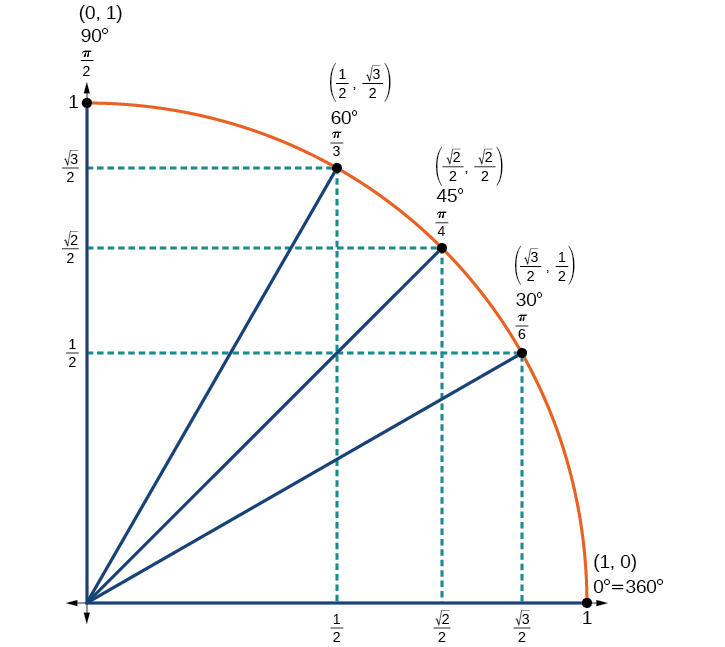
We have now found the cosine and sine values for all of the most commonly encountered angles in the first quadrant of the unit circle. [link] summarizes these values.

Angle

0

\frac{π}{6},

or $30°$

\frac{π}{4},

or $45°$

\frac{π}{3},

or $60°$

\frac{π}{2},

or $90°$


Cosine	1	$\frac{\sqrt{3}}{2}$

\frac{\sqrt{2}}{2}

\frac{1}{2}

0
Sine	0	$\frac{1}{2}$

\frac{\sqrt{2}}{2}

\frac{\sqrt{3}}{2}

[link] shows the common angles in the first quadrant of the unit circle.

Graph of a quarter circle with angles of 0, 30, 45, 60, and 90 degrees inscribed. Equivalence of angles in radians shown. Points along circle are marked.

Using a Calculator to Find Sine and Cosine

To find the cosine and sine of angles other than the special angles, we turn to a computer or calculator. Be aware: Most calculators can be set into “degree” or “radian” mode, which tells the calculator the units for the input value. When we evaluate $\cos (30)$

on our calculator, it will evaluate it as the cosine of 30 degrees if the calculator is in degree mode, or the cosine of 30 radians if the calculator is in radian mode.

Given an angle in radians, use a graphing calculator to find the cosine.

If the calculator has degree mode and radian mode, set it to radian mode.
Press the COS key.
Enter the radian value of the angle and press the close-parentheses key ")".
Press ENTER.

Using a Graphing Calculator to Find Sine and Cosine

Evaluate $\cos (\frac{5 π}{3})$

using a graphing calculator or computer.

Enter the following keystrokes:

COS (5 \times π \div 3 ) ENTER

\cos (\frac{5 π}{3}) = 0.5

Analysis

We can find the cosine or sine of an angle in degrees directly on a calculator with degree mode. For calculators or software that use only radian mode, we can find the sign of $20°,$

for example, by including the conversion factor to radians as part of the input:

SIN (20 \times π \div 180 ) ENTER

Evaluate $\sin (\frac{π}{3}) .$

approximately 0.866025403

Identifying the Domain and Range of Sine and Cosine Functions

Now that we can find the sine and cosine of an angle, we need to discuss their domains and ranges. What are the domains of the sine and cosine functions? That is, what are the smallest and largest numbers that can be inputs of the functions? Because angles smaller than $0$

and angles larger than $2 π$

can still be graphed on the unit circle and have real values of $x, y, and r,$

there is no lower or upper limit to the angles that can be inputs to the sine and cosine functions. The input to the sine and cosine functions is the rotation from the positive x-axis, and that may be any real number.

What are the ranges of the sine and cosine functions? What are the least and greatest possible values for their output? We can see the answers by examining the unit circle, as shown in [link]. The bounds of the x-coordinate are $[−1, 1] .$

The bounds of the y-coordinate are also $[−1, 1] .$

Therefore, the range of both the sine and cosine functions is $[−1, 1] .$

Graph of unit circle.

Finding Reference Angles

We have discussed finding the sine and cosine for angles in the first quadrant, but what if our angle is in another quadrant? For any given angle in the first quadrant, there is an angle in the second quadrant with the same sine value. Because the sine value is the y-coordinate on the unit circle, the other angle with the same sine will share the same y-value, but have the opposite x-value. Therefore, its cosine value will be the opposite of the first angle’s cosine value.

Likewise, there will be an angle in the fourth quadrant with the same cosine as the original angle. The angle with the same cosine will share the same x-value but will have the opposite y-value. Therefore, its sine value will be the opposite of the original angle’s sine value.

As shown in [link], angle $α$

has the same sine value as angle $t;$

the cosine values are opposites. Angle $β$

has the same cosine value as angle $t;$

the sine values are opposites.

\begin{matrix} \sin (t) = \sin (α) & and & \cos (t) = - \cos (α) \\ \sin (t) = - \sin (β) & and & \cos (t) = \cos (β) \end{matrix}

Graph of two side by side circles. First graph has circle with angle t and angle alpha with radius r. Angle t has its terminal side in Quadrant I whereas angle alpha has its terminal side in Quadrant II. Second graph has circle with angle t and angle beta inscribed with radius r. Angle t has its terminal side in Quadrant I whereas angle beta has its terminal side in Quadrant IV.

Recall that an angle’s reference angle is the acute angle, $t,$

formed by the terminal side of the angle $t$

and the horizontal axis. A reference angle is always an angle between $0$

and $90°,$

or $0$

and $\frac{π}{2}$

radians. As we can see from [link], for any angle in quadrants II, III, or IV, there is a reference angle in quadrant I.

Four side-by-side graphs. First graph shows an angle of t in quadrant 1 in its normal position. Second graph shows an angle of t in quadrant 2 due to a rotation of pi minus t. Third graph shows an angle of t in quadrant 3 due to a rotation of t minus pi. Fourth graph shows an angle of t in quadrant 4 due to a rotation of two pi minus t.

**Given an angle between $0$

and $2 π,$

find its reference angle.**

An angle in the first quadrant is its own reference angle.
For an angle in the second or third quadrant, the reference angle is $\| π - t \|$
or
$\| 180° - t \| .$
For an angle in the fourth quadrant, the reference angle is $2 π - t$
or
$360° - t .$
If an angle is less than $0$
or greater than
$2 π,$
add or subtract
$2 π$
as many times as needed to find an equivalent angle between
$0$
and
$2 π .$

Finding a Reference Angle

Find the reference angle of $225°$

as shown in [link].

Graph of circle with 225-degree angle inscribed.

Because $225°$

is in the third quadrant, the reference angle is

\| (180° - 225°) \| = \| - 45° \| = 45°

Find the reference angle of $\frac{5 π}{3} .$

\frac{π}{3}

Using Reference Angles

Now let’s take a moment to reconsider the Ferris wheel introduced at the beginning of this section. Suppose a rider snaps a photograph while stopped twenty feet above ground level. The rider then rotates three-quarters of the way around the circle. What is the rider’s new elevation? To answer questions such as this one, we need to evaluate the sine or cosine functions at angles that are greater than 90 degrees or at a negative angle. Reference angles make it possible to evaluate trigonometric functions for angles outside the first quadrant. They can also be used to find $(x, y)$

coordinates for those angles. We will use the reference angle of the angle of rotation combined with the quadrant in which the terminal side of the angle lies.

Using Reference Angles to Evaluate Trigonometric Functions

We can find the cosine and sine of any angle in any quadrant if we know the cosine or sine of its reference angle. The absolute values of the cosine and sine of an angle are the same as those of the reference angle. The sign depends on the quadrant of the original angle. The cosine will be positive or negative depending on the sign of the x-values in that quadrant. The sine will be positive or negative depending on the sign of the y-values in that quadrant.

Using Reference Angles to Find Cosine and Sine

Angles have cosines and sines with the same absolute value as their reference angles. The sign (positive or negative) can be determined from the quadrant of the angle.

Given an angle in standard position, find the reference angle, and the cosine and sine of the original angle.

Measure the angle between the terminal side of the given angle and the horizontal axis. That is the reference angle.
Determine the values of the cosine and sine of the reference angle.
Give the cosine the same sign as the x-values in the quadrant of the original angle.
Give the sine the same sign as the y-values in the quadrant of the original angle.

Using Reference Angles to Find Sine and Cosine

Using a reference angle, find the exact value of $\cos (150°)$
and
$sin (150°) .$
Using the reference angle, find $\cos \frac{5 π}{4}$
and
$\sin \frac{5 π}{4} .$

$150°$
is located in the second quadrant. The angle it makes with the x-axis is
$180° - 150° = 30°,$
so the reference angle is
$30° .$
This tells us that $150°$

has the same sine and cosine values as $30°,$

except for the sign.

$\begin{matrix} \cos (30°) = \frac{\sqrt{3}}{2} & and & \sin (30°) = \frac{1}{2} \end{matrix}$

Since $150°$

is in the second quadrant, the x-coordinate of the point on the circle is negative, so the cosine value is negative. The y-coordinate is positive, so the sine value is positive.

$\begin{matrix} \cos (150°) = - \frac{\sqrt{3}}{2} & and & \sin (150°) = \frac{1}{2} \end{matrix}$
$\frac{5 π}{4}$
is in the third quadrant. Its reference angle is
$\frac{5 π}{4} - π = \frac{π}{4} .$
The cosine and sine of
$\frac{π}{4}$
are both
$\frac{\sqrt{2}}{2} .$
In the third quadrant, both
$x$
and
$y$
are negative, so:

$\begin{matrix} \cos \frac{5 π}{4} = - \frac{\sqrt{2}}{2} & and & \sin \frac{5 π}{4} = - \frac{\sqrt{2}}{2} \end{matrix}$

Use the reference angle of $315°$
to find
$\cos (315°)$
and
$\sin (315°) .$
Use the reference angle of $- \frac{π}{6}$
to find
$\cos (- \frac{π}{6})$
and
$\sin (- \frac{π}{6}) .$

$cos (315°) = \frac{\sqrt{2}}{2}, sin (315°) = \frac{- \sqrt{2}}{2}$
$cos (- \frac{π}{6}) = \frac{\sqrt{3}}{2}, \sin (- \frac{π}{6}) = - \frac{1}{2}$

Using Reference Angles to Find Coordinates

Now that we have learned how to find the cosine and sine values for special angles in the first quadrant, we can use symmetry and reference angles to fill in cosine and sine values for the rest of the special angles on the unit circle. They are shown in [link]. Take time to learn the $(x, y)$

coordinates of all of the major angles in the first quadrant.

Graph of unit circle with angles in degrees, angles in radians, and points along the circle inscribed.

In addition to learning the values for special angles, we can use reference angles to find $(x, y)$

coordinates of any point on the unit circle, using what we know of reference angles along with the identities

\begin{matrix} x = cos t \\ y = sin t \end{matrix}

First we find the reference angle corresponding to the given angle. Then we take the sine and cosine values of the reference angle, and give them the signs corresponding to the y- and x-values of the quadrant.

**Given the angle of a point on a circle and the radius of the circle, find the $(x, y)$

coordinates of the point.**

Find the reference angle by measuring the smallest angle to the x-axis.
Find the cosine and sine of the reference angle.
Determine the appropriate signs for $x$
and
$y$
in the given quadrant.

Using the Unit Circle to Find Coordinates

Find the coordinates of the point on the unit circle at an angle of $\frac{7 π}{6} .$

We know that the angle $\frac{7 π}{6}$

is in the third quadrant.

First, let’s find the reference angle by measuring the angle to the x-axis. To find the reference angle of an angle whose terminal side is in quadrant III, we find the difference of the angle and $π .$

\frac{7 π}{6} - π = \frac{π}{6}

Next, we will find the cosine and sine of the reference angle.

\begin{matrix} \cos (\frac{π}{6}) = \frac{\sqrt{3}}{2} & \sin (\frac{π}{6}) = \frac{1}{2} \end{matrix}

We must determine the appropriate signs for x and y in the given quadrant. Because our original angle is in the third quadrant, where both $x$

and $y$

are negative, both cosine and sine are negative.

\begin{matrix} \cos (\frac{7 π}{6}) & = & - \frac{\sqrt{3}}{2} \\ \sin (\frac{7 π}{6}) & = & - \frac{1}{2} \end{matrix}

Now we can calculate the $(x, y)$

coordinates using the identities $x = \cos θ$

and $y = \sin θ .$

The coordinates of the point are $(- \frac{\sqrt{3}}{2}, - \frac{1}{2})$

on the unit circle.

Find the coordinates of the point on the unit circle at an angle of $\frac{5 π}{3} .$

(\frac{1}{2}, - \frac{\sqrt{3}}{2})

Access these online resources for additional instruction and practice with sine and cosine functions.

Key Equations

Cosine

\cos t = x


Sine	$\sin t = y$


Pythagorean Identity	$\cos^{2} t + \sin^{2} t = 1$

Key Concepts

Finding the function values for the sine and cosine begins with drawing a unit circle, which is centered at the origin and has a radius of 1 unit.
Using the unit circle, the sine of an angle $t$
equals the y-value of the endpoint on the unit circle of an arc of length
$t$
whereas the cosine of an angle
$t$
equals the x-value of the endpoint. See [link].
The sine and cosine values are most directly determined when the corresponding point on the unit circle falls on an axis. See [link].
When the sine or cosine is known, we can use the Pythagorean Identity to find the other. The Pythagorean Identity is also useful for determining the sines and cosines of special angles. See [link].
Calculators and graphing software are helpful for finding sines and cosines if the proper procedure for entering information is known. See [link].
The domain of the sine and cosine functions is all real numbers.
The range of both the sine and cosine functions is $[−1, 1] .$
The sine and cosine of an angle have the same absolute value as the sine and cosine of its reference angle.
The signs of the sine and cosine are determined from the x- and y-values in the quadrant of the original angle.
An angle’s reference angle is the size angle, $t,$
formed by the terminal side of the angle
$t$
and the horizontal axis. See [link].
Reference angles can be used to find the sine and cosine of the original angle. See [link].
Reference angles can also be used to find the coordinates of a point on a circle. See [link].

Section Exercises

Verbal

Describe the unit circle.

The unit circle is a circle of radius 1 centered at the origin.

What do the x- and y-coordinates of the points on the unit circle represent?

Discuss the difference between a coterminal angle and a reference angle.

Coterminal angles are angles that share the same terminal side. A reference angle is the size of the smallest acute angle, $t,$

formed by the terminal side of the angle $t$

and the horizontal axis.

Explain how the cosine of an angle in the second quadrant differs from the cosine of its reference angle in the unit circle.

Explain how the sine of an angle in the second quadrant differs from the sine of its reference angle in the unit circle.

The sine values are equal.

Algebraic

For the following exercises, use the given sign of the sine and cosine functions to find the quadrant in which the terminal point determined by $t$

lies.

sin (t) < 0

and $cos (t) < 0$

sin (t) > 0

and $\cos (t) > 0$

sin (t) > 0

and $\cos (t) < 0$

sin (t) > 0

and $\cos (t) > 0$

For the following exercises, find the exact value of each trigonometric function.

\sin \frac{π}{2}

\sin \frac{π}{3}

\frac{\sqrt{3}}{2}

\cos \frac{π}{2}

\cos \frac{π}{3}

\frac{1}{2}

\sin \frac{π}{4}

\cos \frac{π}{4}

\frac{\sqrt{2}}{2}

\sin \frac{π}{6}

\sin π

\sin \frac{3 π}{2}

\cos π

-1

\cos 0

\cos \frac{π}{6}

\frac{\sqrt{3}}{2}

\sin 0

Numeric

For the following exercises, state the reference angle for the given angle.

240°

60°

−170°

100°

80 °

−315°

135°

45°

\frac{5 π}{4}

\frac{2 π}{3}

\frac{π}{3}

\frac{5 π}{6}

\frac{- 11 π}{3}

\frac{π}{3}

\frac{−7 π}{4}

\frac{- π}{8}

\frac{π}{8}

For the following exercises, find the reference angle, the quadrant of the terminal side, and the sine and cosine of each angle. If the angle is not one of the angles on the unit circle, use a calculator and round to three decimal places.

225°

300°

60°,

Quadrant IV, $sin (300°) = - \frac{\sqrt{3}}{2}, \cos (300°) = \frac{1}{2}$

320°

135°

45°,

Quadrant II, $sin (135°) = \frac{\sqrt{2}}{2}, \cos (135°) = - \frac{\sqrt{2}}{2}$

210°

120°

60°,

Quadrant II, $sin (120°) = \frac{\sqrt{3}}{2}, \cos (120°) = - \frac{1}{2}$

250°

150°

30°,

Quadrant II, $sin (150°) = \frac{1}{2}, \cos (150°) = - \frac{\sqrt{3}}{2}$

\frac{5 π}{4}

\frac{7 π}{6}

\frac{π}{6},

Quadrant III, $sin (\frac{7 π}{6}) = - \frac{1}{2}, \cos (\frac{7 π}{6}) = - \frac{\sqrt{3}}{2}$

\frac{5 π}{3}

\frac{3 π}{4}

\frac{π}{4},

Quadrant II, $sin (\frac{3 π}{4}) = \frac{\sqrt{2}}{2}, \cos (\frac{4 π}{3}) = - \frac{\sqrt[]{2}}{2}$

\frac{4 π}{3}

\frac{2 π}{3}

\frac{π}{3},

Quadrant II, $sin (\frac{2 π}{3}) = \frac{\sqrt{3}}{2}, \cos (\frac{2 π}{3}) = - \frac{1}{2}$

\frac{5 π}{6}

\frac{7 π}{4}

\frac{π}{4},

Quadrant IV, $sin (\frac{7 π}{4}) = - \frac{\sqrt{2}}{2}, cos (\frac{7 π}{4}) = \frac{\sqrt{2}}{2}$

For the following exercises, find the requested value.

If $cos (t) = \frac{1}{7}$

and $t$

is in the fourth quadrant, find $sin (t) .$

If $cos (t) = \frac{2}{9}$

and $t$

is in the first quadrant, find $sin (t) .$

\frac{\sqrt{77}}{9}

If $sin (t) = \frac{3}{8}$

and $t$

is in the second quadrant, find $cos (t) .$

If $sin (t) = - \frac{1}{4}$

and $t$

is in the third quadrant, find $cos (t) .$

- \frac{\sqrt{15}}{4}

Find the coordinates of the point on a circle with radius 15 corresponding to an angle of $220° .$

Find the coordinates of the point on a circle with radius 20 corresponding to an angle of $120° .$

(−10, 10 \sqrt{3})

Find the coordinates of the point on a circle with radius 8 corresponding to an angle of $\frac{7 π}{4} .$

Find the coordinates of the point on a circle with radius 16 corresponding to an angle of $\frac{5 π}{9} .$

(–2.778, 15.757)

State the domain of the sine and cosine functions.

State the range of the sine and cosine functions.

[–1, 1]

Graphical

For the following exercises, use the given point on the unit circle to find the value of the sine and cosine of $t .$

![Graph of circle with angle of t inscribed. Point of (square root of 2 over 2, square root of 2 over 2) is at the intersection of terminal side of angle and edge of circle](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_02_201.jpg)

![Graph of circle with angle of t inscribed. Point of (negative square root of 3 over 2, 1/2) is at intersection of terminal side of angle and edge of circle.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_02_202.jpg)

\sin t = \frac{1}{2}, \cos t = - \frac{\sqrt{3}}{2}

![Graph of circle with angle of t inscribed. Point of (1/2, negative square root of 3 over 2) is at intersection of terminal side of angle and edge of circle.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_02_203.jpg)

![Graph of circle with angle of t inscribed. Point of (negative square root of 2 over 2, negative square root of 2 over 2) is at intersection of terminal side of angle and edge of circle.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_02_204.jpg)

\sin t = - \frac{\sqrt{2}}{2}, \cos t = - \frac{\sqrt{2}}{2}

![Graph of circle with angle of t inscribed. Point of (1/2, square root of 3 over 2) is at intersection of terminal side of angle and edge of circle.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_02_205.jpg)

![Graph of circle with angle of t inscribed. Point of (-1/2, square root of 3 over 2) is at intersection of terminal side of angle and edge of circle.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_02_206.jpg)

\sin t = \frac{\sqrt{3}}{2}, \cos t = - \frac{1}{2}

![Graph of circle with angle of t inscribed. Point of (-1/2, negative square root of 3 over 2) is at intersection of terminal side of angle and edge of circle.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_02_207.jpg)

![Graph of circle with angle of t inscribed. Point of (square root of 2 over 2, negative square root of 2 over 2) is at intersection of terminal side of angle and edge of circle.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_02_208.jpg)

\sin t = - \frac{\sqrt{2}}{2}, \cos t = \frac{\sqrt{2}}{2}

![Graph of circle with angle of t inscribed. Point of (1,0) is at intersection of terminal side of angle and edge of circle.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_02_209.jpg)

![Graph of circle with angle of t inscribed. Point of (-1,0) is at intersection of terminal side of angle and edge of circle.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_02_210.jpg)

\sin t = 0, \cos t = - 1

![Graph of circle with angle of t inscribed. Point of (0.111,0.994) is at intersection of terminal side of angle and edge of circle.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_02_211.jpg)

![Graph of circle with angle of t inscribed. Point of (0.803,-0.596 is at intersection of terminal side of angle and edge of circle.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_02_212.jpg)

\sin t = - 0.596, \cos t = 0.803

![Graph of circle with angle of t inscribed. Point of (negative square root of 2 over 2, square root of 2 over 2) is at intersection of terminal side of angle and edge of circle.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_02_213.jpg)

![Graph of circle with angle of t inscribed. Point of (square root of 3 over 2, 1/2) is at intersection of terminal side of angle and edge of circle.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_02_214.jpg)

\sin t = \frac{1}{2}, \cos t = \frac{\sqrt{3}}{2}

![Graph of circle with angle of t inscribed. Point of (negative square root of 3 over 2, -1/2) is at intersection of terminal side of angle and edge of circle.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_02_215.jpg)

![Graph of circle with angle of t inscribed. Point of (square root of 3 over 2, -1/2) is at intersection of terminal side of angle and edge of circle.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_02_216.jpg)

\sin t = - \frac{1}{2}, \cos t = \frac{\sqrt{3}}{2}

![Graph of circle with angle of t inscribed. Point of (0, -1) is at intersection of terminal side of angle and edge of circle.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_02_217.jpg)

![Graph of circle with angle of t inscribed. Point of (-0.649, 0.761) is at intersection of terminal side of angle and edge of circle.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_02_218.jpg)

\sin t = 0.761, \cos t = - 0.649

![Graph of circle with angle of t inscribed. Point of (-0.948, -0.317) is at intersection of terminal side of angle and edge of circle.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_02_219.jpg)

![Graph of circle with angle of t inscribed. Point of (0, 1) is at intersection of terminal side of angle and edge of circle.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_02_220.jpg)

\sin t = 1, \cos t = 0

Technology

For the following exercises, use a graphing calculator to evaluate.

\sin \frac{5 π}{9}

\cos \frac{5 π}{9}

−0.1736

\sin \frac{π}{10}

\cos \frac{π}{10}

0.9511

\sin \frac{3 π}{4}

\cos \frac{3 π}{4}

−0.7071

\sin 98°

\cos 98°

−0.1392

\cos 310°

\sin 310°

−0.7660

Extensions

For the following exercises, evaluate.

\sin (\frac{11 π}{3}) \cos (\frac{- 5 π}{6})

\sin (\frac{3 π}{4}) \cos (\frac{5 π}{3})

\frac{\sqrt{2}}{4}

\sin (- \frac{4 π}{3}) \cos (\frac{π}{2})

\sin (\frac{- 9 π}{4}) \cos (\frac{- π}{6})

- \frac{\sqrt{6}}{4}

\sin (\frac{π}{6}) \cos (\frac{- π}{3})

\sin (\frac{7 π}{4}) \cos (\frac{- 2 π}{3})

\frac{\sqrt{2}}{4}

\cos (\frac{5 π}{6}) \cos (\frac{2 π}{3})

\cos (\frac{- π}{3}) \cos (\frac{π}{4})

\frac{\sqrt{2}}{4}

\sin (\frac{- 5 π}{4}) \sin (\frac{11 π}{6})

\sin (π) \sin (\frac{π}{6})

Real-World Applications

For the following exercises, use this scenario: A child enters a carousel that takes one minute to revolve once around. The child enters at the point $(0, 1),$

that is, on the due north position. Assume the carousel revolves counter clockwise.

What are the coordinates of the child after 45 seconds?

What are the coordinates of the child after 90 seconds?

(0, –1)

What are the coordinates of the child after 125 seconds?

When will the child have coordinates $(0.707, –0.707)$

if the ride lasts 6 minutes? (There are multiple answers.)

37.5 seconds, 97.5 seconds, 157.5 seconds, 217.5 seconds, 277.5 seconds, 337.5 seconds

When will the child have coordinates $(–0.866, –0.5)$

if the ride lasts 6 minutes?

Glossary

cosine function: the x-value of the point on a unit circle corresponding to a given angle

Pythagorean Identity: a corollary of the Pythagorean Theorem stating that the square of the cosine of a given angle plus the square of the sine of that angle equals 1

sine function: the y-value of the point on a unit circle corresponding to a given angle

This work is licensed under a Creative Commons Attribution 4.0 International License.

You can also download for free at http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1

Attribution:

For questions regarding this license, please contact partners@openstaxcollege.org.
If you use this textbook as a bibliographic reference, then you should cite it as follows: OpenStax College, Algebra and Trigonometry. OpenStax CNX. http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1.
If you redistribute this textbook in a print format, then you must include on every physical page the following attribution: "Download for free at http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1."
If you redistribute part of this textbook, then you must retain in every digital format page view (including but not limited to EPUB, PDF, and HTML) and on every physical printed page the following attribution: "Download for free at http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1."

Unit Circle

Finding Trigonometric Functions Using the Unit Circle

Defining Sine and Cosine Functions from the Unit Circle

Finding Sines and Cosines of Angles on an Axis

The Pythagorean Identity

Finding Sines and Cosines of Special Angles

Finding Sines and Cosines of 45°

Finding Sines and Cosines of 30°

Using a Calculator to Find Sine and Cosine

Identifying the Domain and Range of Sine and Cosine Functions

Finding Reference Angles

Using Reference Angles

Using Reference Angles to Evaluate Trigonometric Functions

Using Reference Angles to Find Coordinates

Key Equations

Key Concepts

Section Exercises

Verbal

Algebraic

Numeric

Graphical

Technology

Extensions

Real-World Applications

Glossary

Finding Sines and Cosines of $45°$

Finding Sines and Cosines of $30°$