Right Triangle Trigonometry

In this section you will:

Use right triangles to evaluate trigonometric functions.
Find function values for $30° (\frac{π}{6}), 45° (\frac{π}{4}),$
and
$60° (\frac{π}{3}) .$
Use equal cofunctions of complementary angles.
Use the deﬁnitions of trigonometric functions of any angle.
Use right-triangle trigonometry to solve applied problems.

Mt. Everest, which straddles the border between China and Nepal, is the tallest mountain in the world. Measuring its height is no easy task and, in fact, the actual measurement has been a source of controversy for hundreds of years. The measurement process involves the use of triangles and a branch of mathematics known as trigonometry. In this section, we will define a new group of functions known as trigonometric functions, and find out how they can be used to measure heights, such as those of the tallest mountains.

Using Right Triangles to Evaluate Trigonometric Functions

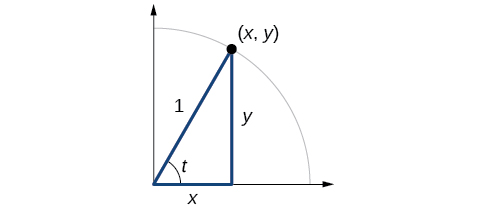
[link] shows a right triangle with a vertical side of length $y$

and a horizontal side has length $x .$

Notice that the triangle is inscribed in a circle of radius 1. Such a circle, with a center at the origin and a radius of 1, is known as a unit circle.

Graph of quarter circle with radius of 1. Inscribed triangle with an angle of t. Point of (x,y) is at intersection of terminal side of angle and edge of circle.

We can define the trigonometric functions in terms an angle t and the lengths of the sides of the triangle. The adjacent side is the side closest to the angle, x. (Adjacent means “next to.”) The opposite side is the side across from the angle, y. The hypotenuse is the side of the triangle opposite the right angle, 1. These sides are labeled in [link].

A right triangle with hypotenuse, opposite, and adjacent sides labeled.

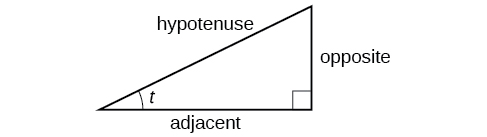
Given a right triangle with an acute angle of $t,$

the first three trigonometric functions are listed.

\begin{matrix} Sine & sin t & = \frac{opposite}{hypotenuse} \end{matrix}

\begin{matrix} Cosine & cos t & = \frac{adjacent}{hypotenuse} \end{matrix}

\begin{matrix} Tangent & tan t & = \frac{opposite}{adjacent} \end{matrix}

A common mnemonic for remembering these relationships is SohCahToa, formed from the first letters of “**S**ine is **o**pposite over **h**ypotenuse, **C**osine is **a**djacent over **h**ypotenuse, **T**angent is **o**pposite over **a**djacent.”

For the triangle shown in [link], we have the following.

\begin{matrix} sin t & = & \frac{y}{1} \\ cos t & = & \frac{x}{1} \\ tan t & = & \frac{y}{x} \end{matrix}

Given the side lengths of a right triangle and one of the acute angles, find the sine, cosine, and tangent of that angle.

Find the sine as the ratio of the opposite side to the hypotenuse.
Find the cosine as the ratio of the adjacent side to the hypotenuse.
Find the tangent as the ratio of the opposite side to the adjacent side.

Evaluating a Trigonometric Function of a Right Triangle

Given the triangle shown in [link], find the value of $\cos α .$

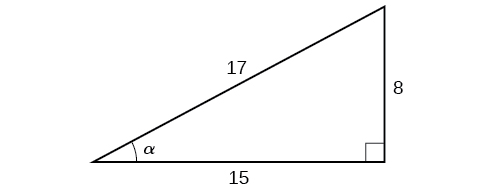
A right triangle with side lengths of 8, 15, and 17. Angle alpha also labeled which is opposite to the side labeled 8.

The side adjacent to the angle is 15, and the hypotenuse of the triangle is 17.

\begin{matrix} \cos (α) & = & \frac{adjacent}{hypotenuse} \\ = & \frac{15}{17} \end{matrix}

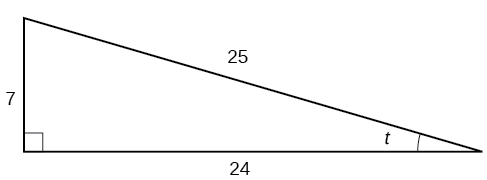
Given the triangle shown in [link], find the value of $sin t .$

A right triangle with sides of 7, 24, and 25. Also labeled is angle t which is opposite the side labeled 7.

\frac{7}{25}

Reciprocal Functions

In addition to sine, cosine, and tangent, there are three more functions. These too are defined in terms of the sides of the triangle.

\begin{matrix} Secant & sec t & = \frac{hypotenuse}{adjacent} \end{matrix}

\begin{matrix} Cosecant & csc t & = \frac{hypotenuse}{opposite} \end{matrix}

\begin{matrix} Cotangent & cot t & = \frac{adjacent}{opposite} \end{matrix}

Take another look at these definitions. These functions are the reciprocals of the first three functions.

\begin{matrix} sin t & = & \frac{1}{csc t} & csc t & = & \frac{1}{sin t} \\ cos t & = & \frac{1}{sec t} & sec t & = & \frac{1}{cos t} \\ tan t & = & \frac{1}{cot t} & cot t & = & \frac{1}{tan t} \end{matrix}

When working with right triangles, keep in mind that the same rules apply regardless of the orientation of the triangle. In fact, we can evaluate the six trigonometric functions of either of the two acute angles in the triangle in [link]. The side opposite one acute angle is the side adjacent to the other acute angle, and vice versa.

Right triangle with angles alpha and beta. Sides are labeled hypotenuse, adjacent to alpha/opposite to beta, and adjacent to beta/opposite alpha.

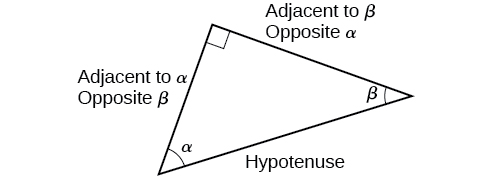
Many problems ask for all six trigonometric functions for a given angle in a triangle. A possible strategy to use is to find the sine, cosine, and tangent of the angles first. Then, find the other trigonometric functions easily using the reciprocals.

Given the side lengths of a right triangle, evaluate the six trigonometric functions of one of the acute angles.

If needed, draw the right triangle and label the angle provided.
Identify the angle, the adjacent side, the side opposite the angle, and the hypotenuse of the right triangle.
Find the required function:
- sine as the ratio of the opposite side to the hypotenuse
- cosine as the ratio of the adjacent side to the hypotenuse
- tangent as the ratio of the opposite side to the adjacent side
- secant as the ratio of the hypotenuse to the adjacent side
- cosecant as the ratio of the hypotenuse to the opposite side
- cotangent as the ratio of the adjacent side to the opposite side

Evaluating Trigonometric Functions of Angles Not in Standard Position

Using the triangle shown in [link], evaluate $\sin α, \cos α, \tan α, \sec α, \csc α, and \cot α .$

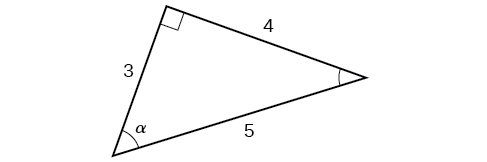
Right triangle with sides of 3, 4, and 5. Angle alpha is also labeled which is opposite the side labeled 4.

\begin{matrix} sin α & = \frac{opposite α}{hypotenuse} & = \frac{4}{5} \\ cos α & = \frac{adjacent to α}{hypotenuse} & = \frac{3}{5} \\ tan α & = \frac{opposite α}{adjacent to α} & = \frac{4}{3} \\ sec α & = \frac{hypotenuse}{adjacent to α} & = \frac{5}{3} \\ csc α & = \frac{hypotenuse}{opposite α} & = \frac{5}{4} \\ cot α & = \frac{adjacent to α}{opposite α} & = \frac{3}{4} \end{matrix}

Analysis

Another approach would have been to find sine, cosine, and tangent first. Then find their reciprocals to determine the other functions.

sec α = \frac{1}{cos α} = \frac{1}{\frac{3}{5}} = \frac{5}{3}

csc α = \frac{1}{csc α} = \frac{1}{\frac{4}{5}} = \frac{5}{4}

cot α = \frac{1}{tan α} = \frac{1}{\frac{4}{3}} = \frac{3}{4}

Using the triangle shown in [link],evaluate $sin t, cos t, tan t, sec t, csc t, and cot t .$

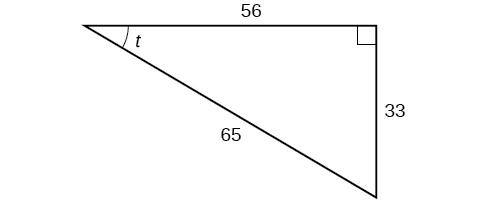
Right triangle with sides 33, 56, and 65. Angle t is also labeled which is opposite to the side labeled 33.

\begin{matrix} sin t & = & \frac{33}{65}, & cos t & = & \frac{56}{65}, & tan t & = & \frac{33}{56}, \\ sec t & = & \frac{65}{56}, & csc t & = & \frac{65}{33}, & cot t & = & \frac{56}{33} \end{matrix}

Finding Trigonometric Functions of Special Angles Using Side Lengths

It is helpful to evaluate the trigonometric functions as they relate to the special angles—multiples of $30°, 60°,$

and $45° .$

Remember, however, that when dealing with right triangles, we are limited to angles between $0° and 90° .$

Suppose we have a $30°, 60°, 90°$

triangle, which can also be described as a $\frac{π}{6}, \frac{π}{3}, \frac{π}{2}$

triangle. The sides have lengths in the relation $s, \sqrt{3} s, 2 s .$

The sides of a $45°, 45°, 90°$

triangle, which can also be described as a $\frac{π}{4}, \frac{π}{4}, \frac{π}{2}$

triangle, have lengths in the relation $s, s, \sqrt{2} s .$

These relations are shown in [link].

Two side-by-side graphs of circles with inscribed angles. First circle has angle of pi/3 inscribed, radius of 2s, base of length s and height of length . Second circle has angle of pi/4 inscribed with radius , base of length s and height of length s.

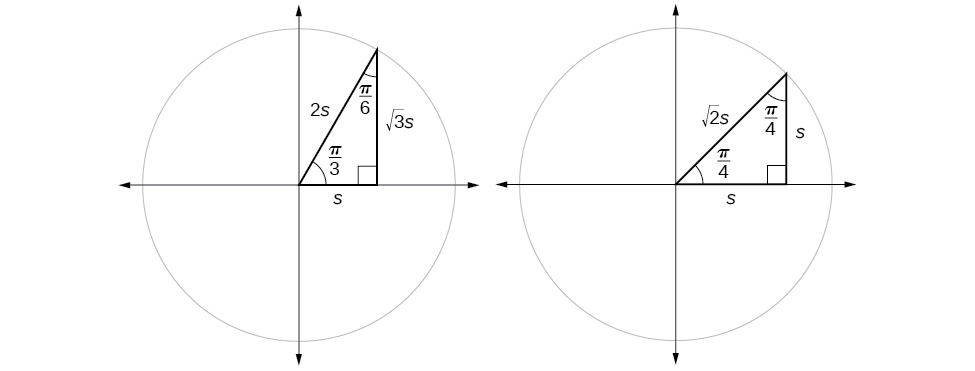
We can then use the ratios of the side lengths to evaluate trigonometric functions of special angles.

Given trigonometric functions of a special angle, evaluate using side lengths.

Use the side lengths shown in [link] for the special angle you wish to evaluate.
Use the ratio of side lengths appropriate to the function you wish to evaluate.

Evaluating Trigonometric Functions of Special Angles Using Side Lengths

Find the exact value of the trigonometric functions of $\frac{π}{3},$

using side lengths.

\begin{matrix} \sin (\frac{π}{3}) & = \frac{opp}{hyp} & = \frac{\sqrt{3 s}}{2 s} & = \frac{\sqrt{3}}{2} \\ \cos (\frac{π}{3}) & = \frac{adj}{hyp} & = \frac{s}{2 s} & = \frac{1}{2} \\ \tan (\frac{π}{3}) & = \frac{opp}{adj} & = \frac{\sqrt{3} s}{s} & = \sqrt{3} \\ \sec (\frac{π}{3}) & = \frac{hyp}{adj} & = \frac{2 s}{s} & = 2 \\ \csc (\frac{π}{3}) & = \frac{hyp}{opp} & = \frac{2 s}{\sqrt{3} s} & = \frac{2}{\sqrt{3}} & = \frac{2 \sqrt{3}}{3} \\ \cot (\frac{π}{3}) & = \frac{adj}{opp} & = \frac{s}{\sqrt{3} s} & = \frac{1}{\sqrt{3}} & = \frac{\sqrt{3}}{3} \end{matrix}

Find the exact value of the trigonometric functions of $\frac{π}{4},$

using side lengths.

\begin{matrix} sin (\frac{π}{4}) & = & \frac{\sqrt{2}}{2}, cos (\frac{π}{4}) = \frac{\sqrt{2}}{2}, \tan (\frac{π}{4}) = 1, \\ sec (\frac{π}{4}) & = & \sqrt{2}, csc (\frac{π}{4}) = \sqrt{2}, cot (\frac{π}{4}) = 1 \end{matrix}

Using Equal Cofunction of Complements

If we look more closely at the relationship between the sine and cosine of the special angles, we notice a pattern. In a right triangle with angles of $\frac{π}{6}$

and $\frac{π}{3},$

we see that the sine of $\frac{π}{3},$

namely $\frac{\sqrt{3}}{2},$

is also the cosine of $\frac{π}{6},$

while the sine of $\frac{π}{6},$

namely $\frac{1}{2},$

is also the cosine of $\frac{π}{3} .$

\begin{matrix} \sin \frac{π}{3} & = \cos \frac{π}{6} & = \frac{\sqrt{3} s}{2 s} & = \frac{\sqrt{3}}{2} \\ \sin \frac{π}{6} & = \cos \frac{π}{3} & = \frac{s}{2 s} & = \frac{1}{2} \end{matrix}

See [link].

A graph of circle with angle pi/3 inscribed with a radius of 2s, a base with length s and a height of.

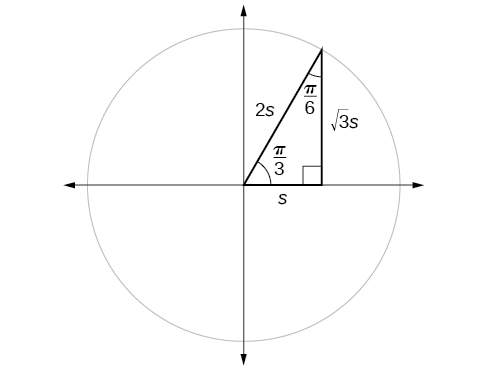
This result should not be surprising because, as we see from [link], the side opposite the angle of $\frac{π}{3}$

is also the side adjacent to $\frac{π}{6},$

so $\sin (\frac{π}{3})$

and $\cos (\frac{π}{6})$

are exactly the same ratio of the same two sides, $\sqrt{3} s$

and $2 s .$

Similarly, $\cos (\frac{π}{3})$

and $\sin (\frac{π}{6})$

are also the same ratio using the same two sides, $s$

and $2 s .$

The interrelationship between the sines and cosines of $\frac{π}{6}$

and $\frac{π}{3}$

also holds for the two acute angles in any right triangle, since in every case, the ratio of the same two sides would constitute the sine of one angle and the cosine of the other. Since the three angles of a triangle add to $π,$

and the right angle is $\frac{π}{2},$

the remaining two angles must also add up to $\frac{π}{2} .$

That means that a right triangle can be formed with any two angles that add to $\frac{π}{2}$

—in other words, any two complementary angles. So we may state a cofunction identity: If any two angles are complementary, the sine of one is the cosine of the other, and vice versa. This identity is illustrated in [link].

Right triangle with angles alpha and beta. Equivalence between sin alpha and cos beta. Equivalence between sin beta and cos alpha.

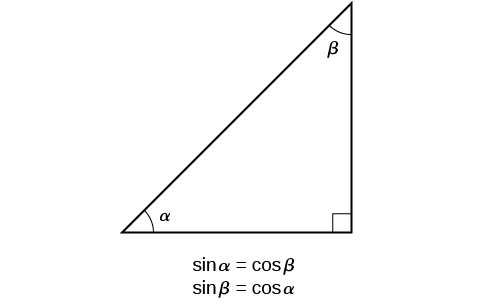
Using this identity, we can state without calculating, for instance, that the sine of $\frac{π}{12}$

equals the cosine of $\frac{5 π}{12},$

and that the sine of $\frac{5 π}{12}$

equals the cosine of $\frac{π}{12} .$

We can also state that if, for a given angle $t, \cos t = \frac{5}{13},$

then $\sin (\frac{π}{2} - t) = \frac{5}{13}$

as well.

Cofunction Identities

The cofunction identities in radians are listed in [link].

\cos t = \sin (\frac{π}{2} - t)

\sin t = \cos (\frac{π}{2} - t)

\tan t = \cot (\frac{π}{2} - t)

\cot t = \tan (\frac{π}{2} - t)

\sec t = \csc (\frac{π}{2} - t)

\csc t = \sec (\frac{π}{2} - t)

Given the sine and cosine of an angle, find the sine or cosine of its complement.

To find the sine of the complementary angle, find the cosine of the original angle.
To find the cosine of the complementary angle, find the sine of the original angle.

Using Cofunction Identities

If $\sin t = \frac{5}{12},$

find $\cos (\frac{π}{2} - t) .$

According to the cofunction identities for sine and cosine, we have the following.

\sin t = \cos (\frac{π}{2} - t)

\cos (\frac{π}{2} - t) = \frac{5}{12}

If $\csc (\frac{π}{6}) = 2,$

find $\sec (\frac{π}{3}) .$

Using Trigonometric Functions

In previous examples, we evaluated the sine and cosine in triangles where we knew all three sides. But the real power of right-triangle trigonometry emerges when we look at triangles in which we know an angle but do not know all the sides.

Given a right triangle, the length of one side, and the measure of one acute angle, find the remaining sides.

For each side, select the trigonometric function that has the unknown side as either the numerator or the denominator. The known side will in turn be the denominator or the numerator.
Write an equation setting the function value of the known angle equal to the ratio of the corresponding sides.
Using the value of the trigonometric function and the known side length, solve for the missing side length.

Finding Missing Side Lengths Using Trigonometric Ratios

Find the unknown sides of the triangle in [link].

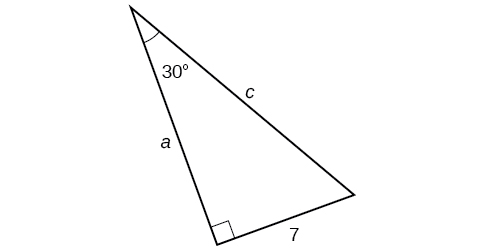
A right triangle with sides a, c, and 7. Angle of 30 degrees is also labeled which is opposite the side labeled 7.

We know the angle and the opposite side, so we can use the tangent to find the adjacent side.

\tan (30°) = \frac{7}{a}

We rearrange to solve for $a .$

\begin{matrix} a & = & \frac{7}{\tan (30°)} \\ \approx & 12.1 \end{matrix}

We can use the sine to find the hypotenuse.

\sin (30°) = \frac{7}{c}

Again, we rearrange to solve for $c .$

\begin{matrix} c & = & \frac{7}{\sin (30°)} \\ = & 14 \end{matrix}

A right triangle has one angle of $\frac{π}{3}$

and a hypotenuse of 20. Find the unknown sides and angle of the triangle.

adjacent = 10; opposite = 10 \sqrt{3};

missing angle is $\frac{π}{6}$

Using Right Triangle Trigonometry to Solve Applied Problems

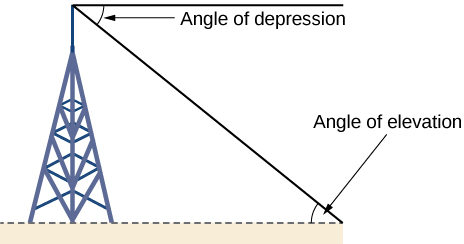
Right-triangle trigonometry has many practical applications. For example, the ability to compute the lengths of sides of a triangle makes it possible to find the height of a tall object without climbing to the top or having to extend a tape measure along its height. We do so by measuring a distance from the base of the object to a point on the ground some distance away, where we can look up to the top of the tall object at an angle. The angle of elevation of an object above an observer relative to the observer is the angle between the horizontal and the line from the object to the observer's eye. The right triangle this position creates has sides that represent the unknown height, the measured distance from the base, and the angled line of sight from the ground to the top of the object. Knowing the measured distance to the base of the object and the angle of the line of sight, we can use trigonometric functions to calculate the unknown height.

Similarly, we can form a triangle from the top of a tall object by looking downward. The angle of depression of an object below an observer relative to the observer is the angle between the horizontal and the line from the object to the observer's eye. See [link].

Diagram of a radio tower with line segments extending from the top and base of the tower to a point on the ground some distance away. The two lines and the tower form a right triangle. The angle near the top of the tower is the angle of depression. The angle on the ground at a distance from the tower is the angle of elevation.

Given a tall object, measure its height indirectly.

Make a sketch of the problem situation to keep track of known and unknown information.
Lay out a measured distance from the base of the object to a point where the top of the object is clearly visible.
At the other end of the measured distance, look up to the top of the object. Measure the angle the line of sight makes with the horizontal.
Write an equation relating the unknown height, the measured distance, and the tangent of the angle of the line of sight.
Solve the equation for the unknown height.

Measuring a Distance Indirectly

To find the height of a tree, a person walks to a point 30 feet from the base of the tree. She measures an angle of $57°$

between a line of sight to the top of the tree and the ground, as shown in [link]. Find the height of the tree.

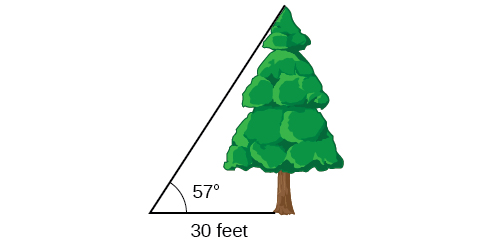
A tree with angle of 57 degrees from vantage point. Vantage point is 30 feet from tree.

We know that the angle of elevation is $57°$

and the adjacent side is 30 ft long. The opposite side is the unknown height.

The trigonometric function relating the side opposite to an angle and the side adjacent to the angle is the tangent. So we will state our information in terms of the tangent of $57°,$

letting $h$

be the unknown height.

\begin{matrix} tan θ & = & \frac{opposite}{adjacent} \\ tan (57°) & = & \frac{h}{30} & Solve for h . \\ h & = & 30tan (57°) & Multiply . \\ h & \approx & 46.2 & Use a calculator . \end{matrix}

The tree is approximately 46 feet tall.

How long a ladder is needed to reach a windowsill 50 feet above the ground if the ladder rests against the building making an angle of $\frac{5 π}{12}$

with the ground? Round to the nearest foot.

About 52 ft

Access these online resources for additional instruction and practice with right triangle trigonometry.

Key Equations

Trigonometric Functions

\begin{matrix} Sine & sin t = \frac{opposite}{hypotenuse} \\ Cosine & cos t = \frac{adjacent}{hypotenuse} \\ Tangent & tan t = \frac{opposite}{adjacent} \\ Secant & sec t = \frac{hypotenuse}{adjacent} \\ Cosecant & csc t = \frac{hypotenuse}{opposite} \\ Cotangent & cot t = \frac{adjacent}{opposite} \end{matrix}


Reciprocal Trigonometric Functions	$\begin{matrix} sin t = \frac{1}{csc t} & csc t = \frac{1}{sin t} \\ cos t = \frac{1}{sec t} & sec t = \frac{1}{cos t} \\ tan t = \frac{1}{cot t} & cot t = \frac{1}{tan t} \end{matrix}$


Cofunction Identities	$\begin{matrix} cos t = \sin (\frac{π}{2} - t) \\ sin t = \cos (\frac{π}{2} - t) \\ tan t = \cot (\frac{π}{2} - t) \\ cot t = \tan (\frac{π}{2} - t) \\ sec t = \csc (\frac{π}{2} - t) \end{matrix}$

Key Concepts

We can define trigonometric functions as ratios of the side lengths of a right triangle. See [link].
The same side lengths can be used to evaluate the trigonometric functions of either acute angle in a right triangle. See [link].
We can evaluate the trigonometric functions of special angles, knowing the side lengths of the triangles in which they occur. See [link].
Any two complementary angles could be the two acute angles of a right triangle.
If two angles are complementary, the cofunction identities state that the sine of one equals the cosine of the other and vice versa. See [link].
We can use trigonometric functions of an angle to find unknown side lengths.
Select the trigonometric function representing the ratio of the unknown side to the known side. See [link].
Right-triangle trigonometry facilitates the measurement of inaccessible heights and distances.
The unknown height or distance can be found by creating a right triangle in which the unknown height or distance is one of the sides, and another side and angle are known. See [link].

Section Exercises

Verbal

For the given right triangle, label the adjacent side, opposite side, and hypotenuse for the indicated angle.

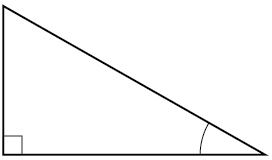
A right triangle.

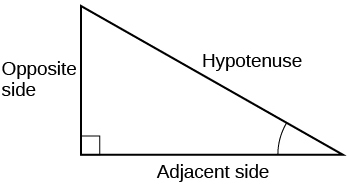
A right triangle with side opposite, adjacent, and hypotenuse labeled.

When a right triangle with a hypotenuse of 1 is placed in a circle of radius 1, which sides of the triangle correspond to the x- and y-coordinates?

The tangent of an angle compares which sides of the right triangle?

The tangent of an angle is the ratio of the opposite side to the adjacent side.

What is the relationship between the two acute angles in a right triangle?

Explain the cofunction identity.

For example, the sine of an angle is equal to the cosine of its complement; the cosine of an angle is equal to the sine of its complement.

Algebraic

For the following exercises, use cofunctions of complementary angles.

\cos (34°) = \sin (\_\_\_°)

\cos (\frac{π}{3}) = \sin (\_\_\_)

\frac{π}{6}

\csc (21°) = \sec (\_\_\_°)

\tan (\frac{π}{4}) = \cot (\_\_\_)

\frac{π}{4}

For the following exercises, find the lengths of the missing sides if side $a$

is opposite angle $A,$

side $b$

is opposite angle $B,$

and side $c$

is the hypotenuse.

\cos B = \frac{4}{5}, a = 10

\sin B = \frac{1}{2}, a = 20

b = \frac{20 \sqrt{3}}{3}, c = \frac{40 \sqrt{3}}{3}

\tan A = \frac{5}{12}, b = 6

\tan A = 100, b = 100

a = 10,000, c = 10,00.5

\sin B = \frac{1}{\sqrt{3}}, a = 2

a = 5, ∡ A = 60°

b = \frac{5 \sqrt{3}}{3}, c = \frac{10 \sqrt{3}}{3}

c = 12, ∡ A = 45°

Graphical

For the following exercises, use [link] to evaluate each trigonometric function of angle $A .$

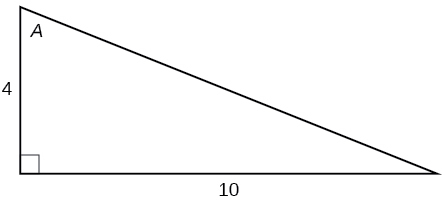
A right triangle with sides 4 and 10 and angle of A labeled which is opposite the side labeled 10.

\sin A

\frac{5 \sqrt{29}}{29}

\cos A

\tan A

\frac{5}{2}

\csc A

\sec A

\frac{\sqrt{29}}{2}

\cot A

For the following exercises, use [link] to evaluate each trigonometric function of angle $A .$

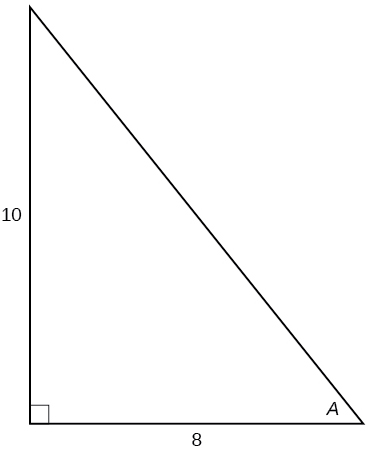
A right triangle with sides of 10 and 8 and angle of A labeled which is opposite the side labeled 10.

\sin A

\frac{5 \sqrt{41}}{41}

\cos A

\tan A

\frac{5}{4}

\csc A

\sec A

\frac{\sqrt{41}}{4}

\cot A

For the following exercises, solve for the unknown sides of the given triangle.

![A right triangle with sides of 7, b, and c labeled. Angles of B and 30 degrees also labeled. The 30 degree angle is opposite the side labeled 7.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_04_205.jpg)

c = 14, b = 7 \sqrt{3}

![A right triangle with sides of 10, a, and c. Angles of 60 degrees and A also labeled. The 60 degree angle is opposite the side labeled 10.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_04_206.jpg)

![A right triangle with corners labeled A, B, and C. Hypotenuse has length of 15 times square root of 2. Angle B is 45 degrees.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_04_207.jpg)

a = 15, b = 15

Technology

For the following exercises, use a calculator to find the length of each side to four decimal places.

![A right triangle with sides of 10, a, and c. Angles of A and 62 degrees are also labeled. The 62 degree angle is opposite the side labeled 10.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_04_208.jpg)

![A right triangle with sides of 7, b, and c. Angles of 35 degrees and B are also labeled.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_04_209.jpg)

b = 9.9970, c = 12.2041

![A right triangle with sides of a, b, and 10 labeled. Angles of 65 degrees and B are also labeled.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_04_210.jpg)

![A right triangle with sides a, b, and 12. Angles of 10 degrees and B are also labeled.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_04_211.jpg)

a = 2.0838, b = 11.8177

![A right triangle with corners labeled A, B, and C. Sides labeled b, c, and 16.5. Angle of 81 degrees also labeled.](/algebra-trigonometry-book/resources/CNX_Precalc_Figure_05_04_212.jpg)

b = 15, ∡ B = 15°

a = 55.9808, c = 57.9555

c = 200, ∡ B = 5°

c = 50, ∡ B = 21°

a = 46.6790, b = 17.9184

a = 30, ∡ A = 27°

b = 3.5, ∡ A = 78°

a = 16.4662, c = 16.8341

Extensions

Find $x .$

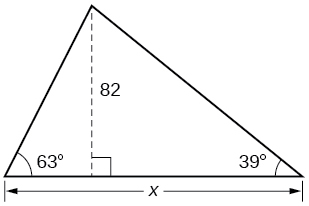
A triangle with angles of 63 degrees and 39 degrees and side x. Bisector in triangle with length of 82.

Find $x .$

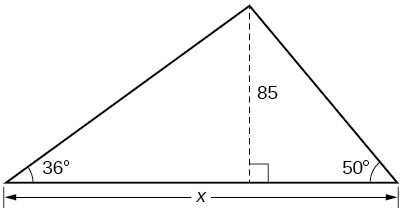
A triangle with angles of 36 degrees and 50 degrees and side x. Bisector in triangle with length of 85.

188.3159

Find $x .$

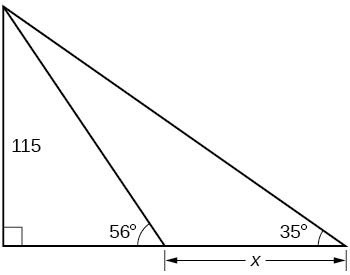
A right triangle with side of 115 and angle of 35 degrees. Within right triangle there is another right triangle with angle of 56 degrees. Side length difference between two triangles is x.

Find $x .$

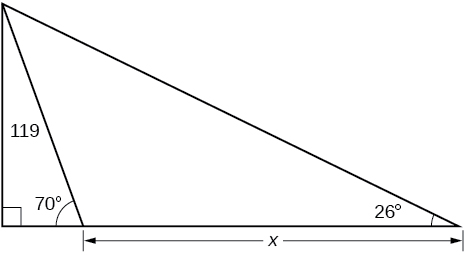
A right triangle with side of 119 and angle of 26 degrees. Within right triangle there is another right triangle with angle of 70 degrees instead of 26 degrees. Difference in side length between two triangles is x.

200.6737

A radio tower is located 400 feet from a building. From a window in the building, a person determines that the angle of elevation to the top of the tower is $36°,$

and that the angle of depression to the bottom of the tower is $23° .$

How tall is the tower?

A radio tower is located 325 feet from a building. From a window in the building, a person determines that the angle of elevation to the top of the tower is $43°,$

and that the angle of depression to the bottom of the tower is $31° .$

How tall is the tower?

498.3471 ft

A 200-foot tall monument is located in the distance. From a window in a building, a person determines that the angle of elevation to the top of the monument is $15°,$

and that the angle of depression to the bottom of the monument is $2° .$

How far is the person from the monument?

A 400-foot tall monument is located in the distance. From a window in a building, a person determines that the angle of elevation to the top of the monument is $18°,$

and that the angle of depression to the bottom of the monument is $3° .$

How far is the person from the monument?

1060.09 ft

There is an antenna on the top of a building. From a location 300 feet from the base of the building, the angle of elevation to the top of the building is measured to be $40° .$

From the same location, the angle of elevation to the top of the antenna is measured to be $43° .$

Find the height of the antenna.

There is lightning rod on the top of a building. From a location 500 feet from the base of the building, the angle of elevation to the top of the building is measured to be $36° .$

From the same location, the angle of elevation to the top of the lightning rod is measured to be $38° .$

Find the height of the lightning rod.

27.372 ft

Real-World Applications

A 33-ft ladder leans against a building so that the angle between the ground and the ladder is $80° .$

How high does the ladder reach up the side of the building?

A 23-ft ladder leans against a building so that the angle between the ground and the ladder is $80° .$

How high does the ladder reach up the side of the building?

22.6506 ft

The angle of elevation to the top of a building in New York is found to be 9 degrees from the ground at a distance of 1 mile from the base of the building. Using this information, find the height of the building.

The angle of elevation to the top of a building in Seattle is found to be 2 degrees from the ground at a distance of 2 miles from the base of the building. Using this information, find the height of the building.

368.7633 ft

Assuming that a 370-foot tall giant redwood grows vertically, if I walk a certain distance from the tree and measure the angle of elevation to the top of the tree to be $60°,$

how far from the base of the tree am I?

Glossary

adjacent side: in a right triangle, the side between a given angle and the right angle

angle of depression: the angle between the horizontal and the line from the object to the observer’s eye, assuming the object is positioned lower than the observer

angle of elevation: the angle between the horizontal and the line from the object to the observer’s eye, assuming the object is positioned higher than the observer

opposite side: in a right triangle, the side most distant from a given angle

hypotenuse: the side of a right triangle opposite the right angle

unit circle: a circle with a center at $(0, 0)$
and radius 1

This work is licensed under a Creative Commons Attribution 4.0 International License.

You can also download for free at http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1

Attribution:

For questions regarding this license, please contact partners@openstaxcollege.org.
If you use this textbook as a bibliographic reference, then you should cite it as follows: OpenStax College, Algebra and Trigonometry. OpenStax CNX. http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1.
If you redistribute this textbook in a print format, then you must include on every physical page the following attribution: "Download for free at http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1."
If you redistribute part of this textbook, then you must retain in every digital format page view (including but not limited to EPUB, PDF, and HTML) and on every physical printed page the following attribution: "Download for free at http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1."