Linear Inequalities and Absolute Value Inequalities

In this section you will:

Use interval notation.
Use properties of inequalities.
Solve inequalities in one variable algebraically.
Solve absolute value inequalities.

Several red winner’s ribbons lie on a white table.

It is not easy to make the honor role at most top universities. Suppose students were required to carry a course load of at least 12 credit hours and maintain a grade point average of 3.5 or above. How could these honor roll requirements be expressed mathematically? In this section, we will explore various ways to express different sets of numbers, inequalities, and absolute value inequalities.

Using Interval Notation

Indicating the solution to an inequality such as $x \geq 4$

can be achieved in several ways.

We can use a number line as shown in [link]. The blue ray begins at $x = 4$

and, as indicated by the arrowhead, continues to infinity, which illustrates that the solution set includes all real numbers greater than or equal to 4.

A number line starting at zero with the last tick mark being labeled 11. There is a dot at the number 4 and an arrow extends toward the right.

We can use set-builder notation: ${x \| x \geq 4},$

which translates to “all real numbers x such that x is greater than or equal to 4.” Notice that braces are used to indicate a set.

The third method is interval notation, in which solution sets are indicated with parentheses or brackets. The solutions to $x \geq 4$

are represented as $[4, \infty) .$

This is perhaps the most useful method, as it applies to concepts studied later in this course and to other higher-level math courses.

The main concept to remember is that parentheses represent solutions greater or less than the number, and brackets represent solutions that are greater than or equal to or less than or equal to the number. Use parentheses to represent infinity or negative infinity, since positive and negative infinity are not numbers in the usual sense of the word and, therefore, cannot be “equaled.” A few examples of an interval, or a set of numbers in which a solution falls, are $[−2, 6),$

or all numbers between $−2$

and $6,$

including $−2,$

but not including $6;$

(- 1, 0),

all real numbers between, but not including $−1$

and $0;$

and $(- \infty, 1],$

all real numbers less than and including $1.$

[link] outlines the possibilities.

Set Indicated	Set-Builder Notation	Interval Notation
All real numbers between a and b, but not including a or b	${x \| a < x < b}$

(a, b)


All real numbers greater than a, but not including a	${x \| x > a}$

(a, \infty)


All real numbers less than b, but not including b	${x \| x < b}$

(- \infty, b)


All real numbers greater than a, including a	${x \| x \geq a}$

[a, \infty)


All real numbers less than b, including b	${x \| x \leq b}$

(- \infty, b]


All real numbers between a and b, including a	${x \| a \leq x < b}$

[a, b)


All real numbers between a and b, including b	${x \| a < x \leq b}$

(a, b]


All real numbers between a and b, including a and b	${x \| a \leq x \leq b}$

[a, b]


All real numbers less than a or greater than b	${x \| x < a or x > b}$

(- \infty, a) \cup (b, \infty)


All real numbers	${x \| x is all real numbers}$

(- \infty, \infty)


{: #Table_02_07_01 summary=”A table with 11 rows and 3 columns. The entries in the first row are: Set Indicated, Set-Builder Notation, Interval Notation. The entries in the second row are: All real numbers between a and b, but not including a and b; {x	a x b}; (a,b). The entries in the third row are: All real numbers greater than a, but not including a; {x	x a}; (a , infinity). The entries in the fourth row are: All real numbers less than b, but not including b; {x	x b}; (negative infinity, b). The entries in the fifth row are: All real numbers greater than a, including a; {x	x a}; [a, infinity). The entries in the sixth row are: All real numbers less than b, including b; {x	x b}; (negative infinity, b]. The entries in the seventh row are: All real numbers between a and b, including a; {x	a x b}; [a, b). The entries in the eighth row are: All real numbers between a and b, including b; {x	a x b}; (a, b]. The entries in the ninth row are: All real numbers between a and b, including a and b; {x	a x b}; [a, b]. The entries in the tenth row are: all real numbers less than a or greater than b; {x	x a or x b}; (negative infinity, a) union (b, infinity). The entries in the eleventh row are: All real numbers; {x	x is all real numbers}; (negative infinity, infinity).”}

Using Interval Notation to Express All Real Numbers Greater Than or Equal to *a*

Use interval notation to indicate all real numbers greater than or equal to $−2.$

Use a bracket on the left of $−2$

and parentheses after infinity: $[−2, \infty) .$

The bracket indicates that $−2$

is included in the set with all real numbers greater than $−2$

to infinity.

Use interval notation to indicate all real numbers between and including $−3$

and $5.$

[−3, 5]

Using Interval Notation to Express All Real Numbers Less Than or Equal to a or Greater Than or Equal to *b*

Write the interval expressing all real numbers less than or equal to $−1$

or greater than or equal to $1.$

We have to write two intervals for this example. The first interval must indicate all real numbers less than or equal to 1. So, this interval begins at $- \infty$

and ends at $−1,$

which is written as $(- \infty, −1] .$

The second interval must show all real numbers greater than or equal to $1,$

which is written as $[1, \infty) .$

However, we want to combine these two sets. We accomplish this by inserting the union symbol, $\cup,$

between the two intervals.

(- \infty, −1] \cup [1, \infty)

Express all real numbers less than $−2$

or greater than or equal to 3 in interval notation.

(- \infty, −2) \cup [3, \infty)

Using the Properties of Inequalities

When we work with inequalities, we can usually treat them similarly to but not exactly as we treat equalities. We can use the addition property and the multiplication property to help us solve them. The one exception is when we multiply or divide by a negative number; doing so reverses the inequality symbol.

Properties of Inequalities

\begin{array}{l} A d d i t i o n P r o p e r t y & If a < b, then a + c < b + c . \\ M u l t i p l i c a t i o n P r o p e r t y & If a < b and c > 0, then a c < b c . \\ If a < b and c < 0, then a c > b c . \end{array}

These properties also apply to $a \leq b,$

a > b,

and $a \geq b .$

Demonstrating the Addition Property

Illustrate the addition property for inequalities by solving each of the following:

(a) $x - 15 < 4$
(b) $6 \geq x - 1$
(c) $x + 7 > 9$

The addition property for inequalities states that if an inequality exists, adding or subtracting the same number on both sides does not change the inequality.

$\begin{array}{l} x - 15 < 4 \\ x - 15 + 15 < 4 + 15 & Add 15 to both sides . \\ x < 19 \end{array}$
$\begin{array}{l} 6 \geq x - 1 \\ 6 + 1 \geq x - 1 + 1 & Add 1 to both sides . \\ 7 \geq x \end{array}$
$\begin{array}{l} x + 7 > 9 \\ x + 7 - 7 > 9 - 7 & Subtract 7 from both sides . \\ x > 2 \end{array}$

Solve: $3 x −2 < 1.$

x < 1

Demonstrating the Multiplication Property

Illustrate the multiplication property for inequalities by solving each of the following:

$3 x < 6$
$−2 x - 1 \geq 5$
$5 - x > 10$

$\begin{array}{l} 3 x < 6 \\ \frac{1}{3} (3 x) < (6) \frac{1}{3} \\ x < 2 \end{array}$
$\begin{array}{l} - 2 x - 1 \geq 5 \\ - 2 x \geq 6 \\ (- \frac{1}{2}) (- 2 x) \geq (6) (- \frac{1}{2}) & Multiply by - \frac{1}{2} . \\ x \leq - 3 & Reverse the inequality . \end{array}$
$\begin{array}{l} 5 - x > 10 \\ - x > 5 \\ (- 1) (- x) > (5) (- 1) & Multiply by - 1. \\ x < - 5 & Reverse the inequality . \end{array}$

Solve: $4 x + 7 \geq 2 x - 3.$

x \geq −5

Solving Inequalities in One Variable Algebraically

As the examples have shown, we can perform the same operations on both sides of an inequality, just as we do with equations; we combine like terms and perform operations. To solve, we isolate the variable.

Solving an Inequality Algebraically

Solve the inequality: $13 - 7 x \geq 10 x - 4.$

Solving this inequality is similar to solving an equation up until the last step.

\begin{array}{l} 13 - 7 x \geq 10 x - 4 \\ 13 - 17 x \geq −4 & Move variable terms to one side of the inequality . \\ −17 x \geq −17 & Isolate the variable term . \\ x \leq 1 & Dividing both sides by −17 reverses the inequality . \end{array}

The solution set is given by the interval $(- \infty, 1],$

or all real numbers less than and including 1.

Solve the inequality and write the answer using interval notation: $- x + 4 < \frac{1}{2} x + 1.$

(2, \infty)

Solving an Inequality with Fractions

Solve the following inequality and write the answer in interval notation: $- \frac{3}{4} x \geq - \frac{5}{8} + \frac{2}{3} x .$

We begin solving in the same way we do when solving an equation.

\begin{array}{l} - \frac{3}{4} x \geq - \frac{5}{8} + \frac{2}{3} x \\ - \frac{3}{4} x - \frac{2}{3} x \geq - \frac{5}{8} & Put variable terms on one side . \\ - \frac{9}{12} x - \frac{8}{12} x \geq - \frac{5}{8} & Write fractions with common denominator . \\ - \frac{17}{12} x \geq - \frac{5}{8} \\ x \leq - \frac{5}{8} (- \frac{12}{17}) & Multiplying by a negative number reverses the inequality . \\ x \leq \frac{15}{34} \end{array}

The solution set is the interval $(- \infty, \frac{15}{34}] .$

Solve the inequality and write the answer in interval notation: $- \frac{5}{6} x \leq \frac{3}{4} + \frac{8}{3} x .$

[- \frac{3}{14}, \infty)

Understanding Compound Inequalities

A compound inequality includes two inequalities in one statement. A statement such as $4 < x \leq 6$

means $4 < x$

and $x \leq 6.$

There are two ways to solve compound inequalities: separating them into two separate inequalities or leaving the compound inequality intact and performing operations on all three parts at the same time. We will illustrate both methods.

Solving a Compound Inequality

Solve the compound inequality: $3 \leq 2 x + 2 < 6.$

The first method is to write two separate inequalities: $3 \leq 2 x + 2$

and $2 x + 2 < 6.$

We solve them independently.

\begin{array}{l} 3 \leq 2 x + 2 & and & 2 x + 2 < 6 \\ 1 \leq 2 x & 2 x < 4 \\ \frac{1}{2} \leq x & x < 2 \end{array}

Then, we can rewrite the solution as a compound inequality, the same way the problem began.

\frac{1}{2} \leq x < 2

In interval notation, the solution is written as $[\frac{1}{2}, 2) .$

The second method is to leave the compound inequality intact, and perform solving procedures on the three parts at the same time.

\begin{array}{l} 3 \leq 2 x + 2 < 6 \\ 1 \leq 2 x < 4 & Isolate the variable term, and subtract 2 from all three parts . \\ \frac{1}{2} \leq x < 2 & Divide through all three parts by 2 . \end{array}

We get the same solution: $[\frac{1}{2}, 2) .$

Solve the compound inequality: $4 < 2 x - 8 \leq 10.$

6 < x \leq 9 ​ ​ or (6, 9]

Solving a Compound Inequality with the Variable in All Three Parts

Solve the compound inequality with variables in all three parts: $3 + x > 7 x - 2 > 5 x - 10.$

Let’s try the first method. Write two inequalities:

\begin{array}{l} 3 + x > 7 x - 2 & and & 7 x - 2 > 5 x - 10 \\ 3 > 6 x - 2 & 2 x - 2 > −10 \\ 5 > 6 x & 2 x > −8 \\ \frac{5}{6} > x & x > −4 \\ x < \frac{5}{6} & −4 < x \end{array}

The solution set is $−4 < x < \frac{5}{6}$

or in interval notation $(−4, \frac{5}{6}) .$

Notice that when we write the solution in interval notation, the smaller number comes first. We read intervals from left to right, as they appear on a number line. See [link].

A number line with the points -4 and 5/6 labeled. Dots appear at these points and a line connects these two dots.

Solve the compound inequality: $3 y < 4 - 5 y < 5 + 3 y .$

(- \frac{1}{8}, \frac{1}{2})

Solving Absolute Value Inequalities

As we know, the absolute value of a quantity is a positive number or zero. From the origin, a point located at $(- x, 0)$

has an absolute value of $x,$

as it is x units away. Consider absolute value as the distance from one point to another point. Regardless of direction, positive or negative, the distance between the two points is represented as a positive number or zero.

An absolute value inequality is an equation of the form

\| A \| < B, \| A \| \leq B, \| A \| > B, or \| A \| \geq B,

Where A, and sometimes B, represents an algebraic expression dependent on a variable x. Solving the inequality means finding the set of all $x$

-values that satisfy the problem. Usually this set will be an interval or the union of two intervals and will include a range of values.

There are two basic approaches to solving absolute value inequalities: graphical and algebraic. The advantage of the graphical approach is we can read the solution by interpreting the graphs of two equations. The advantage of the algebraic approach is that solutions are exact, as precise solutions are sometimes difficult to read from a graph.

Suppose we want to know all possible returns on an investment if we could earn some amount of money within $200 of $600. We can solve algebraically for the set of x-values such that the distance between $x$

and 600 is less than 200. We represent the distance between $x$

and 600 as $\| x - 600 \|,$

and therefore, $\| x - 600 \| \leq 200$

\begin{matrix} −200 \leq x - 600 \leq 200 \\ −200 + 600 \leq x - 600 + 600 \leq 200 + 600 \\ 400 \leq x \leq 800 \end{matrix}

This means our returns would be between $400 and $800.

To solve absolute value inequalities, just as with absolute value equations, we write two inequalities and then solve them independently.

Absolute Value Inequalities

For an algebraic expression X, and $k > 0,$

an absolute value inequality is an inequality of the form

\begin{array}{l} \| X \| < k is equivalent to - k < X < k \\ \| X \| > k is equivalent to X < - k or X > k \end{array}

These statements also apply to $\| X \| \leq k$

and $\| X \| \geq k .$

Determining a Number within a Prescribed Distance

Describe all values $x$

within a distance of 4 from the number 5.

We want the distance between $x$

and 5 to be less than or equal to 4. We can draw a number line, such as in [link], to represent the condition to be satisfied.

A number line with one tick mark in the center labeled: 5. The tick marks on either side of the center one are not marked. Arrows extend from the center tick mark to the outer tick marks, both are labeled 4.

The distance from $x$

to 5 can be represented using an absolute value symbol, $\| x - 5 \| .$

Write the values of $x$

that satisfy the condition as an absolute value inequality.

\| x - 5 \| \leq 4

We need to write two inequalities as there are always two solutions to an absolute value equation.

\begin{array}{l} x - 5 \leq 4 & and & x - 5 \geq - 4 \\ x \leq 9 & x \geq 1 \end{array}

If the solution set is $x \leq 9$

and $x \geq 1,$

then the solution set is an interval including all real numbers between and including 1 and 9.

So $\| x - 5 \| \leq 4$

is equivalent to $[1, 9]$

in interval notation.

Describe all x-values within a distance of 3 from the number 2.

\| x −2 \| \leq 3

Solving an Absolute Value Inequality

Solve $\| x - 1 \| \leq 3$

\begin{array}{l} \| x - 1 \| \leq 3 \\ −3 \leq x - 1 \leq 3 \\ −2 \leq x \leq 4 \\ [−2, 4] \end{array}

Using a Graphical Approach to Solve Absolute Value Inequalities

Given the equation $y = - \frac{1}{2} \| 4 x - 5 \| + 3,$

determine the x-values for which the y-values are negative.

We are trying to determine where $y < 0,$

which is when $- \frac{1}{2} \| 4 x - 5 \| + 3 < 0.$

We begin by isolating the absolute value.

\begin{array}{l} - \frac{1}{2} \| 4 x - 5 \| < - 3 & Multiply both sides by –2, and reverse the inequality . \\ \| 4 x - 5 \| > 6 \end{array}

Next, we solve for the equality $\| 4 x - 5 \| = 6.$

\begin{array}{l} 4 x - 5 = 6 & 4 x - 5 = - 6 \\ 4 x = 11 & or & 4 x = - 1 \\ x = \frac{11}{4} & x = - \frac{1}{4} \end{array}

Now, we can examine the graph to observe where the y-values are negative. We observe where the branches are below the x-axis. Notice that it is not important exactly what the graph looks like, as long as we know that it crosses the horizontal axis at $x = - \frac{1}{4}$

and $x = \frac{11}{4},$

and that the graph opens downward. See [link].

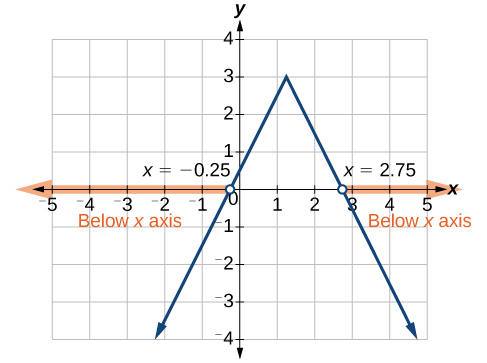
A coordinate plan with the x-axis ranging from -5 to 5 and the y-axis ranging from -4 to 4. The function y = -1/2|4x – 5| + 3 is graphed. An open circle appears at the point -0.25 and an arrow

Solve $- 2 \| k - 4 \| \leq - 6.$

k \leq 1

or $k \geq 7;$

in interval notation, this would be $(- \infty, 1] \cup [7, \infty) .$

A coordinate plane with the x-axis ranging from -1 to 9 and the y-axis ranging from -3 to 8. The function y = -2|k 4| + 6 is graphed and everything above the function is shaded in.

Access these online resources for additional instruction and practice with linear inequalities and absolute value inequalities.

Key Concepts

Interval notation is a method to indicate the solution set to an inequality. Highly applicable in calculus, it is a system of parentheses and brackets that indicate what numbers are included in a set and whether the endpoints are included as well. See [link] and [link].
Solving inequalities is similar to solving equations. The same algebraic rules apply, except for one: multiplying or dividing by a negative number reverses the inequality. See [link], [link], [link], and [link].
Compound inequalities often have three parts and can be rewritten as two independent inequalities. Solutions are given by boundary values, which are indicated as a beginning boundary or an ending boundary in the solutions to the two inequalities. See [link] and [link].
Absolute value inequalities will produce two solution sets due to the nature of absolute value. We solve by writing two equations: one equal to a positive value and one equal to a negative value. See [link] and [link].
Absolute value inequalities can also be solved by graphing. At least we can check the algebraic solutions by graphing, as we cannot depend on a visual for a precise solution. See [link].

Section Exercises

Verbal

When solving an inequality, explain what happened from Step 1 to Step 2:

\begin{array}{l} Step 1 & - 2 x > 6 \\ Step 2 & x < - 3 \end{array}

When we divide both sides by a negative it changes the sign of both sides so the sense of the inequality sign changes.

When solving an inequality, we arrive at:

\begin{array}{l} x + 2 < x + 3 \\ 2 < 3 \end{array}

Explain what our solution set is.

When writing our solution in interval notation, how do we represent all the real numbers?

(- \infty, \infty)

When solving an inequality, we arrive at:

\begin{array}{l} x + 2 > x + 3 \\ 2 > 3 \end{array}

Explain what our solution set is.

Describe how to graph $y = \| x - 3 \|$

We start by finding the x-intercept, or where the function = 0. Once we have that point, which is $(3, 0),$

we graph to the right the straight line graph $y = x −3,$

and then when we draw it to the left we plot positive y values, taking the absolute value of them.

Algebraic

For the following exercises, solve the inequality. Write your final answer in interval notation.

4 x - 7 \leq 9

3 x + 2 \geq 7 x - 1

(- \infty, \frac{3}{4}]

−2 x + 3 > x - 5

4 (x + 3) \geq 2 x - 1

[\frac{- 13}{2}, \infty)

- \frac{1}{2} x \leq \frac{- 5}{4} + \frac{2}{5} x

−5 (x - 1) + 3 > 3 x - 4 - 4 x

(- \infty, 3)

−3 (2 x + 1) > −2 (x + 4)

\frac{x + 3}{8} - \frac{x + 5}{5} \geq \frac{3}{10}

(- \infty, - \frac{37}{3}]

\frac{x - 1}{3} + \frac{x + 2}{5} \leq \frac{3}{5}

For the following exercises, solve the inequality involving absolute value. Write your final answer in interval notation.

\| x + 9 \| \geq −6

All real numbers $(- \infty, \infty)$

\| 2 x + 3 \| < 7

\| 3 x - 1 \| > 11

(- \infty, \frac{- 10}{3}) \cup (4, \infty)

\| 2 x + 1 \| + 1 \leq 6

\| x - 2 \| + 4 \geq 10

(- \infty, −4] \cup [8, + \infty)

\| −2 x + 7 \| \leq 13

\| x - 7 \| < −4

No solution

\| x - 20 \| > −1

\| \frac{x - 3}{4} \| < 2

(−5, 11)

For the following exercises, describe all the x-values within or including a distance of the given values.

Distance of 5 units from the number 7

Distance of 3 units from the number 9

[6, 12]

Distance of10 units from the number 4

Distance of 11 units from the number 1

[−10, 12]

For the following exercises, solve the compound inequality. Express your answer using inequality signs, and then write your answer using interval notation.

−4 < 3 x + 2 \leq 18

3 x + 1 > 2 x - 5 > x - 7

\begin{array}{l} x > - 6 and x > - 2 & Take the intersection of two sets . \\ x > - 2, (- 2, + \infty) \end{array}

3 y < 5 - 2 y < 7 + y

2 x - 5 < −11 or 5 x + 1 \geq 6

\begin{array}{l} x < - 3 or x \geq 1 & Take the union of the two sets . \\ (- \infty, - 3) {\cup^{​}}^{​} [1, \infty) \end{array}

x + 7 < x + 2

Graphical

For the following exercises, graph the function. Observe the points of intersection and shade the x-axis representing the solution set to the inequality. Show your graph and write your final answer in interval notation.

\| x - 1 \| > 2

(- \infty, −1) \cup (3, \infty)

A coordinate plane where the x and y axes both range from -10 to 10. The function |x 1| is graphed and labeled along with the line y = 2. Along the x-axis there is an open circle at the point -1 with an arrow extending leftward from it. Also along the x-axis is an open circle at the point 3 with an arrow extending rightward from it.

\| x + 3 \| \geq 5

\| x + 7 \| \leq 4

[−11, −3]

A coordinate plane with the x-axis ranging from -14 to 10 and the y-axis ranging from -1 to 10. The function y = |x + 7| and the line y = 4 are graphed. On the x-axis theres a dot on the points -11 and -3 with a line connecting them.

\| x - 2 \| < 7

\| x - 2 \| < 0

It is never less than zero. No solution.

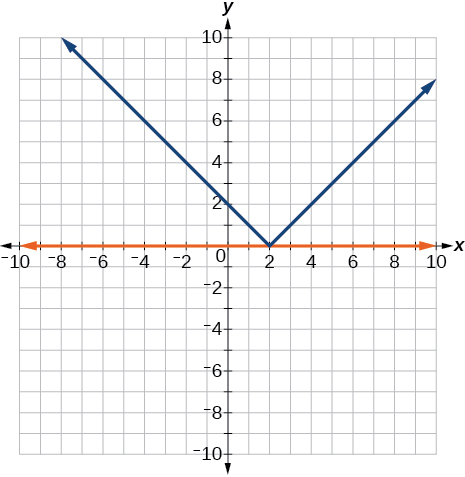
A coordinate plane with the x and y axes ranging from -10 to 10. The function y = |x -2| and the line y = 0 are graphed.

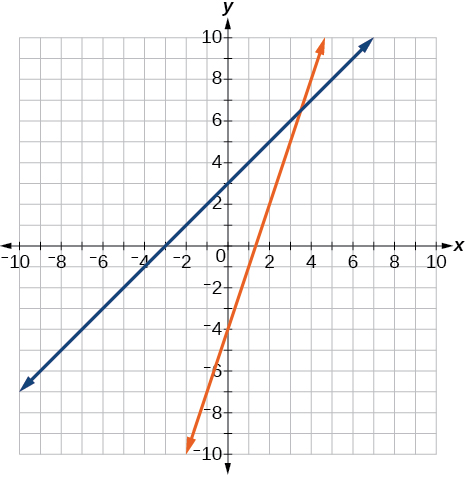
For the following exercises, graph both straight lines (left-hand side being y1 and right-hand side being y2) on the same axes. Find the point of intersection and solve the inequality by observing where it is true comparing the y-values of the lines.

x + 3 < 3 x - 4

x - 2 > 2 x + 1

Where the blue line is above the orange line; point of intersection is $x = - 3.$

(- \infty, −3)

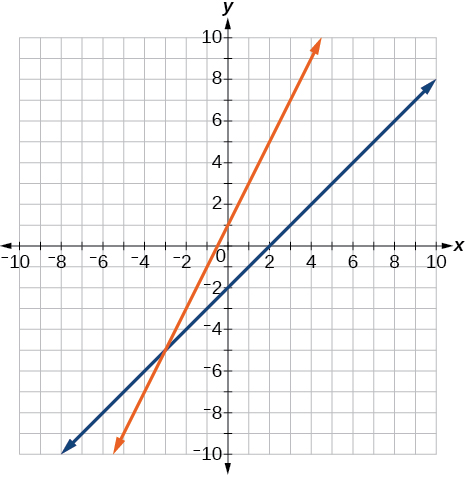
A coordinate plane with the x and y axes ranging from -10 to 10. The lines y = x - 2 and y = 2x + 1 are graphed on the same axes.

x + 1 > x + 4

\frac{1}{2} x + 1 > \frac{1}{2} x - 5

Where the blue line is above the orange line; always. All real numbers.

(- \infty, - \infty)

A coordinate plane with the x and y axes ranging from -10 to 10. The lines y = x/2 +1 and y = x/2 5 are both graphed on the same axes.

4 x + 1 < \frac{1}{2} x + 3

Numeric

For the following exercises, write the set in interval notation.

{x \| −1 < x < 3}

(−1, 3)

{x \| x \geq 7}

{x \| x < 4}

(- \infty, 4)

{x \| x is all real numbers}

For the following exercises, write the interval in set-builder notation.

(- \infty, 6)

{x \| x < 6}

(4, + \infty)

[−3, 5)

{x \| −3 \leq x < 5}

[−4, 1] \cup [9, \infty)

For the following exercises, write the set of numbers represented on the number line in interval notation.

![A number line with two tick marks labeled: -2 and 1 respectively. There is an open circle around the -2 and a dot on the 1 with an arrow connecting the two.](/algebra-trigonometry-book/resources/CNX_CAT_Figure_02_07_211.jpg)

(−2, 1]

![Number line with two tick marks labeled: -1 and 2 respectively. There is an open circle around the tick mark labeled -1 and a line that extends leftward from the circle. There is a dot around the tick mark labeled 2 and a line that extends rightward from the dot.](/algebra-trigonometry-book/resources/CNX_CAT_Figure_02_07_212.jpg)

![Number line with one tick mark labeled 4. There is a dot on the tick mark and an arrow extending leftward from the dot.](/algebra-trigonometry-book/resources/CNX_CAT_Figure_02_07_213.jpg)

(- \infty, 4]

Technology

For the following exercises, input the left-hand side of the inequality as a Y1 graph in your graphing utility. Enter y2 = the right-hand side. Entering the absolute value of an expression is found in the MATH menu, Num, 1:abs(. Find the points of intersection, recall (2^nd CALC 5:intersection, 1^st curve, enter, 2^nd curve, enter, guess, enter). Copy a sketch of the graph and shade the x-axis for your solution set to the inequality. Write final answers in interval notation.

\| x + 2 \| - 5 < 2

\frac{- 1}{2} \| x + 2 \| < 4

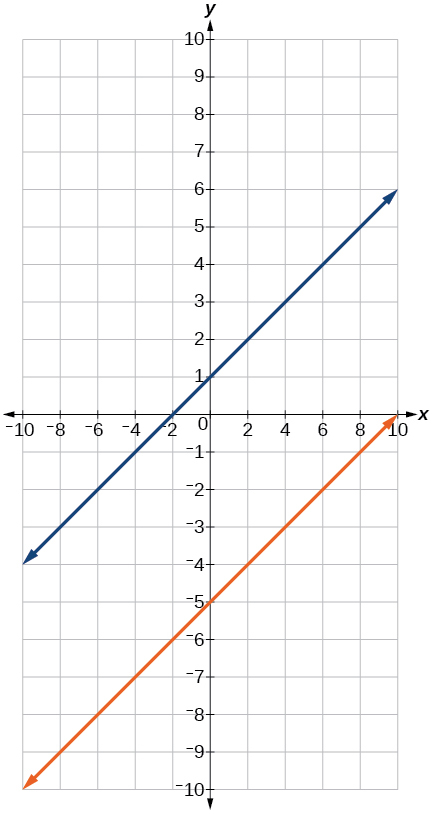
Where the blue is below the orange; always. All real numbers. $(- \infty, + \infty) .$

A coordinate plane with the x and y axes ranging from -10 to 10. The function y = -0.5|x + 2| and the line y = 4 are graphed on the same axes. A line runs along the entire x-axis.

\| 4 x + 1 \| - 3 > 2

\| x - 4 \| < 3

Where the blue is below the orange; $(1, 7) .$

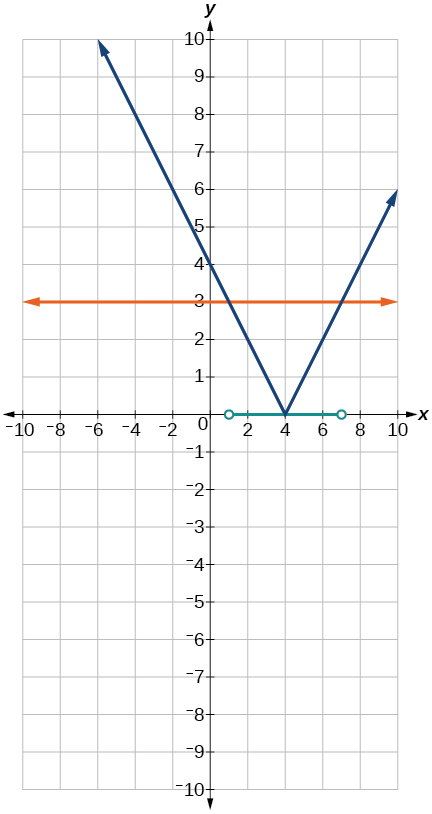
A coordinate plane with the x and y axes ranging from -10 to 10. The function y = |x 4| and the line y = 3 are graphed on the same axes. Along the x-axis the points 1 and 7 have an open circle around them and a line connects the two.

\| x + 2 \| \geq 5

Extensions

Solve $\| 3 x + 1 \| = \| 2 x + 3 \|$

x = 2, \frac{- 4}{5}

Solve $x^{2} - x > 12$

\frac{x - 5}{x + 7} \leq 0,

x \neq −7

(−7, 5]

p = - x^{2} + 130 x - 3000

is a profit formula for a small business. Find the set of x-values that will keep this profit positive.

Real-World Applications

In chemistry the volume for a certain gas is given by $V = 20 T,$

where V is measured in cc and T is temperature in ºC. If the temperature varies between 80ºC and 120ºC, find the set of volume values.

\begin{array}{l} 80 \leq T \leq 120 \\ 1, 600 \leq 20 T \leq 2, 400 \end{array}

[1, 600, 2, 400]

A basic cellular package costs $20/mo. for 60 min of calling, with an additional charge of $.30/min beyond that time.. The cost formula would be $C = $ 20 + .30 (x - 60) .$

If you have to keep your bill lower than $50, what is the maximum calling minutes you can use?

Chapter Review Exercises

The Rectangular Coordinate Systems and Graphs

For the following exercises, find the x-intercept and the y-intercept without graphing.

4 x - 3 y = 12

x-intercept: $(3, 0);$

y-intercept: $(0, −4)$

2 y - 4 = 3 x

For the following exercises, solve for y in terms of x, putting the equation in slope–intercept form.

5 x = 3 y - 12

y = \frac{5}{3} x + 4

2 x - 5 y = 7

For the following exercises, find the distance between the two points.

(−2, 5) (4, −1)

\sqrt{72} = 6 \sqrt{2}

(−12, −3) (−1, 5)

Find the distance between the two points $(−71,432)$

and $(511,218)$

using your calculator, and round your answer to the nearest thousandth.

620.097

For the following exercises, find the coordinates of the midpoint of the line segment that joins the two given points.

(−1, 5) and (4, 6)

(−13, 5) and (17, 18)

midpoint is $(2, \frac{23}{2})$

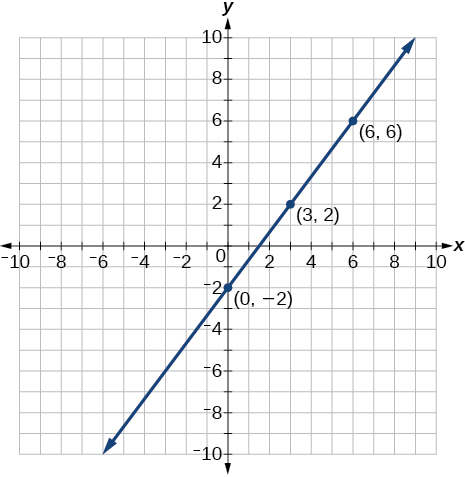
For the following exercises, construct a table and graph the equation by plotting at least three points.

y = \frac{1}{2} x + 4

4 x - 3 y = 6


x	y
0	−2
3	2
6	6

A coordinate plane with the x and y axes ranging from -10 to 10. The points (0,-2); (3,2) and (6,6) are plotted and a line runs through all these points.

Linear Equations in One Variable

For the following exercises, solve for $x .$

5 x + 2 = 7 x - 8

3 (x + 2) - 10 = x + 4

x = 4

7 x - 3 = 5

12 - 5 (x + 1) = 2 x - 5

x = \frac{12}{7}

\frac{2 x}{3} - \frac{3}{4} = \frac{x}{6} + \frac{21}{4}

For the following exercises, solve for $x .$

State all x-values that are excluded from the solution set.

\frac{x}{x^{2} - 9} + \frac{4}{x + 3} = \frac{3}{x^{2} - 9}

x \neq 3, −3

No solution

\frac{1}{2} + \frac{2}{x} = \frac{3}{4}

For the following exercises, find the equation of the line using the point-slope formula.

Passes through these two points: $(−2, 1), (4, 2) .$

y = \frac{1}{6} x + \frac{4}{3}

Passes through the point $(- 3, 4)$

and has a slope of $\frac{- 1}{3} .$

Passes through the point $(- 3, 4)$

and is parallel to the graph $y = \frac{2}{3} x + 5.$

y = \frac{2}{3} x + 6

Passes through these two points: $(5, 1), (5, 7) .$

Models and Applications

For the following exercises, write and solve an equation to answer each question.

The number of males in the classroom is five more than three times the number of females. If the total number of students is 73, how many of each gender are in the class?

females 17, males 56

A man has 72 ft. of fencing to put around a rectangular garden. If the length is 3 times the width, find the dimensions of his garden.

A truck rental is $25 plus $.30/mi. Find out how many miles Ken traveled if his bill was $50.20.

84 mi

Complex Numbers

For the following exercises, use the quadratic equation to solve.

x^{2} - 5 x + 9 = 0

2 x^{2} + 3 x + 7 = 0

x = \frac{- 3}{4} \pm \frac{i \sqrt{47}}{4}

For the following exercises, name the horizontal component and the vertical component.

4 - 3 i

−2 - i

horizontal component $−2;$

vertical component $−1$

For the following exercises, perform the operations indicated.

(9 - i) - (4 - 7 i)

(2 + 3 i) - (- 5 - 8 i)

7 + 11 i

2 \sqrt{- 75} + 3 \sqrt{25}

\sqrt{- 16} + 4 \sqrt{- 9}

16 i

- 6 i (i - 5)

{(3 - 5 i)}^{2}

−16 - 30 i

\sqrt{- 4} \cdot \sqrt{- 12}

\sqrt{- 2} (\sqrt{- 8} - \sqrt{5})

−4 - i \sqrt{10}

\frac{2}{5 - 3 i}

\frac{3 + 7 i}{i}

x = 7 - 3 i

Quadratic Equations

For the following exercises, solve the quadratic equation by factoring.

2 x^{2} - 7 x - 4 = 0

3 x^{2} + 18 x + 15 = 0

x = −1, −5

25 x^{2} - 9 = 0

7 x^{2} - 9 x = 0

x = 0, \frac{9}{7}

For the following exercises, solve the quadratic equation by using the square-root property.

x^{2} = 49

{(x - 4)}^{2} = 36

x = 10, −2

For the following exercises, solve the quadratic equation by completing the square.

x^{2} + 8 x - 5 = 0

4 x^{2} + 2 x - 1 = 0

x = \frac{- 1 \pm \sqrt{5}}{4}

For the following exercises, solve the quadratic equation by using the quadratic formula. If the solutions are not real, state No real solution.

2 x^{2} - 5 x + 1 = 0

15 x^{2} - x - 2 = 0

x = \frac{2}{5}, \frac{- 1}{3}

For the following exercises, solve the quadratic equation by the method of your choice.

{(x - 2)}^{2} = 16

x^{2} = 10 x + 3

x = 5 \pm 2 \sqrt{7}

Other Types of Equations

For the following exercises, solve the equations.

x^{\frac{3}{2}} = 27

x^{\frac{1}{2}} - 4 x^{\frac{1}{4}} = 0

x = 0, 256

4 x^{3} + 8 x^{2} - 9 x - 18 = 0

3 x^{5} - 6 x^{3} = 0

x = 0, \pm \sqrt{2}

\sqrt{x + 9} = x - 3

\sqrt{3 x + 7} + \sqrt{x + 2} = 1

x = −2

\| 3 x - 7 \| = 5

\| 2 x + 3 \| - 5 = 9

x = \frac{11}{2}, \frac{−17}{2}

Linear Inequalities and Absolute Value Inequalities

For the following exercises, solve the inequality. Write your final answer in interval notation.

5 x - 8 \leq 12

- 2 x + 5 > x - 7

(- \infty, 4)

\frac{x - 1}{3} + \frac{x + 2}{5} \leq \frac{3}{5}

\| 3 x + 2 \| + 1 \leq 9

[\frac{- 10}{3}, 2]

\| 5 x - 1 \| > 14

\| x - 3 \| < −4

No solution

For the following exercises, solve the compound inequality. Write your answer in interval notation.

−4 < 3 x + 2 \leq 18

3 y < 1 - 2 y < 5 + y

(- \frac{4}{3}, \frac{1}{5})

For the following exercises, graph as described.

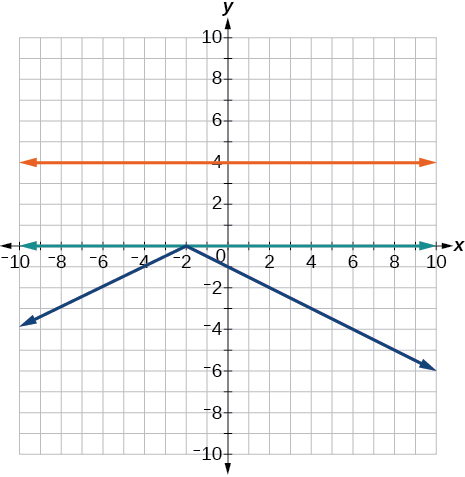
Graph the absolute value function and graph the constant function. Observe the points of intersection and shade the x-axis representing the solution set to the inequality. Show your graph and write your final answer in interval notation.

\| x + 3 \| \geq 5

Graph both straight lines (left-hand side being y1 and right-hand side being y2) on the same axes. Find the point of intersection and solve the inequality by observing where it is true comparing the y-values of the lines. See the interval where the inequality is true.

x + 3 < 3 x - 4

Where the blue is below the orange line; point of intersection is $x = 3.5.$

(3.5, \infty)

A coordinate plane with the x and y axes ranging from -10 to 10. The lines y = x + 3 and y = 3x -4 graphed on the same axes.

Chapter Practice Test

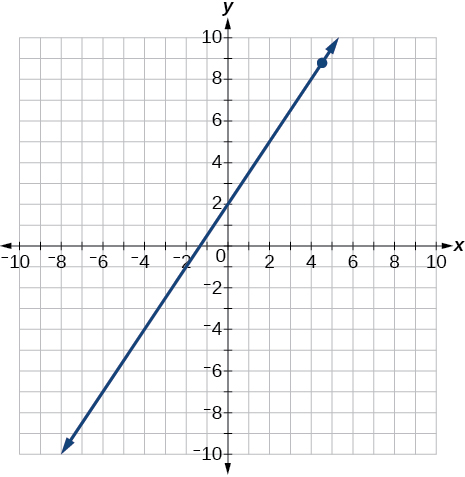
Graph the following: $2 y = 3 x + 4.$

y = \frac{3}{2} x + 2


x	y
0	2
2	5
4	8

A coordinate plane with the x and y axes ranging from -10 to 10. The line going through the points (0,2); (2,5); and (4,8) is graphed.

Find the x- and y-intercepts for the following:

2 x - 5 y = 6

Find the x- and y-intercepts of this equation, and sketch the graph of the line using just the intercepts plotted.

3 x - 4 y = 12

(0, −3)

(4, 0)

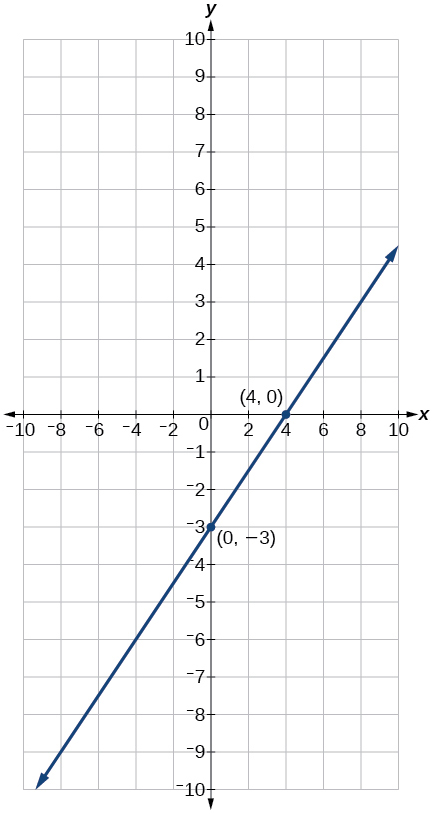
A coordinate plane with the x and y axes ranging from -10 to 10. The points (4,0) and (0,-3) are plotted with a line running through them.

Find the exact distance between $(5, −3)$

and $(- 2, 8) .$

Find the coordinates of the midpoint of the line segment joining the two points.

Write the interval notation for the set of numbers represented by ${x \| x \leq 9} .$

(- \infty, 9]

Solve for x: $5 x + 8 = 3 x - 10.$

Solve for x: $3 (2 x - 5) - 3 (x - 7) = 2 x - 9.$

x = −15

Solve for x: $\frac{x}{2} + 1 = \frac{4}{x}$

Solve for x: $\frac{5}{x + 4} = 4 + \frac{3}{x - 2} .$

x \neq −4, 2;

x = \frac{- 5}{2}, 1

The perimeter of a triangle is 30 in. The longest side is 2 less than 3 times the shortest side and the other side is 2 more than twice the shortest side. Find the length of each side.

Solve for x. Write the answer in simplest radical form.

\frac{x^{2}}{3} - x = \frac{−1}{2}

x = \frac{3 \pm \sqrt{3}}{2}

Solve: $3 x - 8 \leq 4.$

Solve: $\| 2 x + 3 \| < 5.$

(−4, 1)

Solve: $\| 3 x - 2 \| \geq 4.$

For the following exercises, find the equation of the line with the given information.

Passes through the points $(- 4, 2)$

and $(5, −3) .$

y = \frac{−5}{9} x - \frac{2}{9}

Has an undefined slope and passes through the point $(4, 3) .$

Passes through the point $(2, 1)$

and is perpendicular to $y = \frac{- 2}{5} x + 3.$

y = \frac{5}{2} x - 4

Add these complex numbers: $(3 - 2 i) + (4 - i) .$

Simplify: $\sqrt{−4} + 3 \sqrt{−16} .$

14 i

Multiply: $5 i (5 - 3 i) .$

Divide: $\frac{4 - i}{2 + 3 i} .$

\frac{5}{13} - \frac{14}{13} i

Solve this quadratic equation and write the two complex roots in $a + b i$

form: $x^{2} - 4 x + 7 = 0.$

Solve: ${(3 x - 1)}^{2} - 1 = 24.$

x = 2, \frac{- 4}{3}

Solve: $x^{2} - 6 x = 13.$

Solve: $4 x^{2} - 4 x - 1 = 0$

x = \frac{1}{2} \pm \frac{\sqrt{2}}{2}

Solve:

\sqrt{x - 7} = x - 7

Solve: $2 + \sqrt{12 - 2 x} = x$

4

Solve: ${(x - 1)}^{\frac{2}{3}} = 9$

For the following exercises, find the real solutions of each equation by factoring.

2 x^{3} - x^{2} - 8 x + 4 = 0

x = \frac{1}{2}, 2, −2

{(x + 5)}^{2} - 3 (x + 5) - 4 = 0

Glossary

compound inequality: a problem or a statement that includes two inequalities

interval: an interval describes a set of numbers within which a solution falls

interval notation: a mathematical statement that describes a solution set and uses parentheses or brackets to indicate where an interval begins and ends

linear inequality: similar to a linear equation except that the solutions will include sets of numbers

This work is licensed under a Creative Commons Attribution 4.0 International License.

You can also download for free at http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1

Attribution:

For questions regarding this license, please contact partners@openstaxcollege.org.
If you use this textbook as a bibliographic reference, then you should cite it as follows: OpenStax College, Algebra and Trigonometry. OpenStax CNX. http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1.
If you redistribute this textbook in a print format, then you must include on every physical page the following attribution: "Download for free at http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1."
If you redistribute part of this textbook, then you must retain in every digital format page view (including but not limited to EPUB, PDF, and HTML) and on every physical printed page the following attribution: "Download for free at http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1."