Factoring Polynomials

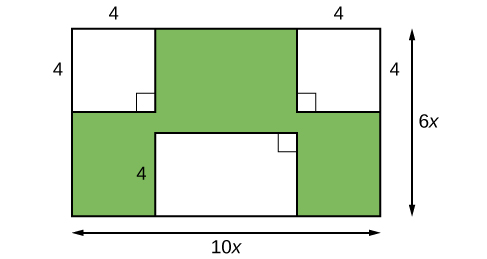
Imagine that we are trying to find the area of a lawn so that we can determine how much grass seed to purchase. The lawn is the green portion in [link].

The area of the entire region can be found using the formula for the area of a rectangle.

The areas of the portions that do not require grass seed need to be subtracted from the area of the entire region. The two square regions each have an area of

A = s^{2} = 4^{2} = 16

units². So the region that must be subtracted has an area of

2 (16) + 40 x - 32 = 40 x

The area of the region that requires grass seed is found by subtracting

60 x^{2} - 40 x

Many polynomial expressions can be written in simpler forms by factoring. In this section, we will look at a variety of methods that can be used to factor polynomial expressions.

Factoring the Greatest Common Factor of a Polynomial

When we study fractions, we learn that the greatest common factor (GCF) of two numbers is the largest number that divides evenly into both numbers. For instance,

4

When factoring a polynomial expression, our first step should be to check for a GCF. Look for the GCF of the coefficients, and then look for the GCF of the variables.

Factoring the Greatest Common Factor

Factor $6 x^{3} y^{3} + 45 x^{2} y^{2} + 21 x y .$

First, find the GCF of the expression. The GCF of $6, 45,$

and $21$

is $3.$

The GCF of $x^{3}, x^{2},$

and $x$

is $x .$

(Note that the GCF of a set of expressions in the form $x^{n}$

will always be the exponent of lowest degree.) And the GCF of $y^{3}, y^{2},$

and $y$

is $y .$

Combine these to find the GCF of the polynomial, $3 x y .$

Next, determine what the GCF needs to be multiplied by to obtain each term of the polynomial. We find that $3 x y (2 x^{2} y^{2}) = 6 x^{3} y^{3}, 3 x y (15 x y) = 45 x^{2} y^{2},$

and $3 x y (7) = 21 x y .$

Finally, write the factored expression as the product of the GCF and the sum of the terms we needed to multiply by.

(3 x y) (2 x^{2} y^{2} + 15 x y + 7)

Analysis

After factoring, we can check our work by multiplying. Use the distributive property to confirm that $(3 x y) (2 x^{2} y^{2} + 15 x y + 7) = 6 x^{3} y^{3} + 45 x^{2} y^{2} + 21 x y .$

Factoring a Trinomial with Leading Coefficient 1

Although we should always begin by looking for a GCF, pulling out the GCF is not the only way that polynomial expressions can be factored. The polynomial

x^{2} + 5 x + 6

Factoring a Trinomial with Leading Coefficient 1

Factor $x^{2} + 2 x - 15.$

We have a trinomial with leading coefficient $1, b = 2,$

and $c = −15.$

We need to find two numbers with a product of $−15$

and a sum of $2.$

In [link], we list factors until we find a pair with the desired sum.


Factors of $−15$	Sum of Factors
$1, −15$	$−14$
$−1, 15$	14
$3, −5$	$−2$
$−3, 5$	2

Now that we have identified $p$

and $q$

as $−3$

and $5,$

write the factored form as $(x - 3) (x + 5) .$

Analysis

We can check our work by multiplying. Use FOIL to confirm that $(x - 3) (x + 5) = x^{2} + 2 x - 15.$

Factoring by Grouping

Trinomials with leading coefficients other than 1 are slightly more complicated to factor. For these trinomials, we can factor by grouping by dividing the x term into the sum of two terms, factoring each portion of the expression separately, and then factoring out the GCF of the entire expression. The trinomial

2 x^{2} + 5 x + 3

using this process. We begin by rewriting the original expression as

2 x^{2} + 2 x + 3 x + 3

and then factor each portion of the expression to obtain

2 x (x + 1) + 3 (x + 1) .

Factoring a Trinomial by Grouping

Factor $5 x^{2} + 7 x - 6$

by grouping.

We have a trinomial with $a = 5, b = 7,$

and $c = −6.$

First, determine $a c = −30.$

We need to find two numbers with a product of $−30$

and a sum of $7.$

In [link], we list factors until we find a pair with the desired sum.


Factors of $−30$	Sum of Factors
$1, −30$	$−29$
$−1, 30$	29
$2, −15$	$−13$
$−2, 15$	13
$3, −10$	$−7$
$−3, 10$	7

So $p = −3$

and $q = 10.$

\begin{matrix} 5 x^{2} - 3 x + 10 x - 6 & Rewrite the original expression as a x^{2} + p x + q x + c . \\ x (5 x - 3) + 2 (5 x - 3) & Factor out the GCF of each part . \\ (5 x - 3) (x + 2) & Factor out the GCF ​ of the expression . \end{matrix}

Analysis

We can check our work by multiplying. Use FOIL to confirm that $(5 x - 3) (x + 2) = 5 x^{2} + 7 x - 6.$

Factoring a Perfect Square Trinomial

A perfect square trinomial is a trinomial that can be written as the square of a binomial. Recall that when a binomial is squared, the result is the square of the first term added to twice the product of the two terms and the square of the last term.

Factoring a Difference of Squares

A difference of squares is a perfect square subtracted from a perfect square. Recall that a difference of squares can be rewritten as factors containing the same terms but opposite signs because the middle terms cancel each other out when the two factors are multiplied.

Factoring the Sum and Difference of Cubes

Now, we will look at two new special products: the sum and difference of cubes. Although the sum of squares cannot be factored, the sum of cubes can be factored into a binomial and a trinomial.

Similarly, the sum of cubes can be factored into a binomial and a trinomial, but with different signs.

We can use the acronym SOAP to remember the signs when factoring the sum or difference of cubes. The first letter of each word relates to the signs: Same Opposite Always Positive. For example, consider the following example.

Factoring Expressions with Fractional or Negative Exponents

Expressions with fractional or negative exponents can be factored by pulling out a GCF. Look for the variable or exponent that is common to each term of the expression and pull out that variable or exponent raised to the lowest power. These expressions follow the same factoring rules as those with integer exponents. For instance,

2 x^{\frac{1}{4}} + 5 x^{\frac{3}{4}}

Key Equations

Verbal

If the terms of a polynomial do not have a GCF, does that mean it is not factorable? Explain.

The terms of a polynomial do not have to have a common factor for the entire polynomial to be factorable. For example, $4 x^{2}$

and $−9 y^{2}$

don’t have a common factor, but the whole polynomial is still factorable: $4 x^{2} −9 y^{2} = (2 x + 3 y) (2 x −3 y) .$

A polynomial is factorable, but it is not a perfect square trinomial or a difference of two squares. Can you factor the polynomial without finding the GCF?

How do you factor by grouping?

Divide the $x$

term into the sum of two terms, factor each portion of the expression separately, and then factor out the GCF of the entire expression.

Algebraic

For the following exercises, find the greatest common factor.

14 x + 4 x y - 18 x y^{2}

49 m b^{2} - 35 m^{2} b a + 77 m a^{2}

7 m

30 x^{3} y - 45 x^{2} y^{2} + 135 x y^{3}

200 p^{3} m^{3} - 30 p^{2} m^{3} + 40 m^{3}

10 m^{3}

36 j^{4} k^{2} - 18 j^{3} k^{3} + 54 j^{2} k^{4}

6 y^{4} - 2 y^{3} + 3 y^{2} - y

y

For the following exercises, factor by grouping.

6 x^{2} + 5 x - 4

2 a^{2} + 9 a - 18

(2 a −3) (a + 6)

6 c^{2} + 41 c + 63

6 n^{2} - 19 n - 11

(3 n −11) (2 n + 1)

20 w^{2} - 47 w + 24

2 p^{2} - 5 p - 7

(p + 1) (2 p −7)

For the following exercises, factor the polynomial.

7 x^{2} + 48 x - 7

10 h^{2} - 9 h - 9

(5 h + 3) (2 h −3)

2 b^{2} - 25 b - 247

9 d^{2} −73 d + 8

(9 d −1) (d −8)

90 v^{2} −181 v + 90

12 t^{2} + t - 13

(12 t + 13) (t −1)

2 n^{2} - n - 15

16 x^{2} - 100

(4 x + 10) (4 x - 10)

25 y^{2} - 196

121 p^{2} - 169

(11 p + 13) (11 p - 13)

4 m^{2} - 9

361 d^{2} - 81

(19 d + 9) (19 d - 9)

324 x^{2} - 121

144 b^{2} - 25 c^{2}

(12 b + 5 c) (12 b - 5 c)

16 a^{2} - 8 a + 1

49 n^{2} + 168 n + 144

{(7 n + 12)}^{2}

121 x^{2} - 88 x + 16

225 y^{2} + 120 y + 16

{(15 y + 4)}^{2}

m^{2} - 20 m + 100

25 p^{2} - 120 m + 144

{(5 p - 12)}^{2}

36 q^{2} + 60 q + 25

For the following exercises, factor the polynomials.

x^{3} + 216

(x + 6) (x^{2} - 6 x + 36)

27 y^{3} - 8

125 a^{3} + 343

(5 a + 7) (25 a^{2} - 35 a + 49)

b^{3} - 8 d^{3}

64 x^{3} −125

(4 x - 5) (16 x^{2} + 20 x + 25)

729 q^{3} + 1331

125 r^{3} + 1,728 s^{3}

(5 r + 12 s) (25 r^{2} - 60 r s + 144 s^{2})

4 x {(x - 1)}^{- \frac{2}{3}} + 3 {(x - 1)}^{\frac{1}{3}}

3 c {(2 c + 3)}^{- \frac{1}{4}} - 5 {(2 c + 3)}^{\frac{3}{4}}

{(2 c + 3)}^{- \frac{1}{4}} (−7 c - 15)

3 t {(10 t + 3)}^{\frac{1}{3}} + 7 {(10 t + 3)}^{\frac{4}{3}}

14 x {(x + 2)}^{- \frac{2}{5}} + 5 {(x + 2)}^{\frac{3}{5}}

{(x + 2)}^{- \frac{2}{5}} (19 x + 10)

9 y {(3 y - 13)}^{\frac{1}{5}} - 2 {(3 y - 13)}^{\frac{6}{5}}

5 z {(2 z - 9)}^{- \frac{3}{2}} + 11 {(2 z - 9)}^{- \frac{1}{2}}

{(2 z - 9)}^{- \frac{3}{2}} (27 z - 99)

6 d {(2 d + 3)}^{- \frac{1}{6}} + 5 {(2 d + 3)}^{\frac{5}{6}}

Real-World Applications

For the following exercises, consider this scenario:

Charlotte has appointed a chairperson to lead a city beautification project. The first act is to install statues and fountains in one of the city’s parks. The park is a rectangle with an area of $98 x^{2} + 105 x - 27$

m², as shown in the figure below. The length and width of the park are perfect factors of the area.

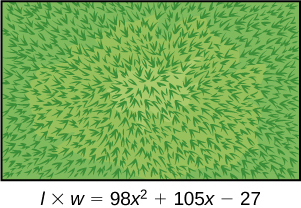
A rectangle that’s textured to look like a field. The field is labeled: l times w = ninety-eight times x squared plus one hundred five times x minus twenty-seven.

Factor by grouping to find the length and width of the park.

(14 x −3) (7 x + 9)

A statue is to be placed in the center of the park. The area of the base of the statue is $4 x^{2} + 12 x + 9 m^{2} .$

Factor the area to find the lengths of the sides of the statue.

At the northwest corner of the park, the city is going to install a fountain. The area of the base of the fountain is $9 x^{2} - 25 m^{2} .$

Factor the area to find the lengths of the sides of the fountain.

(3 x + 5) (3 x −5)

For the following exercise, consider the following scenario:

A school is installing a flagpole in the central plaza. The plaza is a square with side length 100 yd. as shown in the figure below. The flagpole will take up a square plot with area $x^{2} - 6 x + 9$

yd².

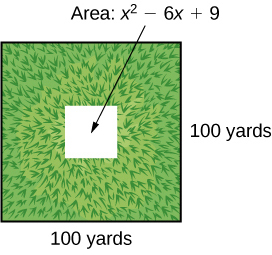
A square that’s textured to look like a field with a missing piece in the shape of a square in the center. The sides of the larger square are labeled: 100 yards. The center square is labeled: Area: x squared minus six times x plus nine.

Find the length of the base of the flagpole by factoring.

Extensions

For the following exercises, factor the polynomials completely.

16 x^{4} - 200 x^{2} + 625

{(2 x + 5)}^{2} {(2 x - 5)}^{2}

81 y^{4} - 256

16 z^{4} - 2,401 a^{4}

(4 z^{2} + 49 a^{2}) (2 z + 7 a) (2 z - 7 a)

5 x {(3 x + 2)}^{- \frac{2}{4}} + {(12 x + 8)}^{\frac{3}{2}}

{(32 x^{3} + 48 x^{2} - 162 x - 243)}^{−1}

\frac{1}{(4 x + 9) (4 x −9) (2 x + 3)}


perfect square trinomial	$a^{2} + 2 a b + b^{2} = {(a + b)}^{2}$


difference of cubes	$a^{3} - b^{3} = (a - b) (a^{2} + a b + b^{2})$

Factoring the Greatest Common Factor of a Polynomial

Factoring a Trinomial with Leading Coefficient 1

Factoring by Grouping

Factoring a Perfect Square Trinomial

Factoring a Difference of Squares

Factoring the Sum and Difference of Cubes

Factoring Expressions with Fractional or Negative Exponents

Key Equations

Verbal

Algebraic

Real-World Applications

Extensions

Glossary