Binomial Theorem

In this section, you will:

Apply the Binomial Theorem.

A polynomial with two terms is called a binomial. We have already learned to multiply binomials and to raise binomials to powers, but raising a binomial to a high power can be tedious and time-consuming. In this section, we will discuss a shortcut that will allow us to find ${(x + y)}^{n}$

without multiplying the binomial by itself $n$

times.

Identifying Binomial Coefficients

In Counting Principles, we studied combinations. In the shortcut to finding ${(x + y)}^{n},$

we will need to use combinations to find the coefficients that will appear in the expansion of the binomial. In this case, we use the notation $(\begin{matrix} n \\ r \end{matrix})$

instead of $C (n, r),$

but it can be calculated in the same way. So

(\begin{matrix} n \\ r \end{matrix}) = C (n, r) = \frac{n!}{r! (n - r)!}

The combination $(\begin{matrix} n \\ r \end{matrix})$

is called a binomial coefficient. An example of a binomial coefficient is $(\begin{matrix} 5 \\ 2 \end{matrix}) = C (5, 2) = 10.$

Binomial Coefficients

If $n$

and $r$

are integers greater than or equal to 0 with $n \geq r,$

then the binomial coefficient is

(\begin{matrix} n \\ r \end{matrix}) = C (n, r) = \frac{n!}{r! (n - r)!}

Is a binomial coefficient always a whole number?

Yes. Just as the number of combinations must always be a whole number, a binomial coefficient will always be a whole number.

Finding Binomial Coefficients

Find each binomial coefficient.

$(\begin{matrix} 5 \\ 3 \end{matrix})$
$(\begin{matrix} 9 \\ 2 \end{matrix})$
$(\begin{matrix} 9 \\ 7 \end{matrix})$

Use the formula to calculate each binomial coefficient. You can also use the $n C_{r}$

function on your calculator.

(\begin{matrix} n \\ r \end{matrix}) = C (n, r) = \frac{n!}{r! (n - r)!}

$(\begin{matrix} 5 \\ 3 \end{matrix}) = \frac{5!}{3! (5 - 3)!} = \frac{5 \cdot 4 \cdot 3!}{3! 2!} = 10$
$(\begin{matrix} 9 \\ 2 \end{matrix}) = \frac{9!}{2! (9 - 2)!} = \frac{9 \cdot 8 \cdot 7!}{2! 7!} = 36$
$(\begin{matrix} 9 \\ 7 \end{matrix}) = \frac{9!}{7! (9 - 7)!} = \frac{9 \cdot 8 \cdot 7!}{7! 2!} = 36$

Analysis

Notice that we obtained the same result for parts (b) and (c). If you look closely at the solution for these two parts, you will see that you end up with the same two factorials in the denominator, but the order is reversed, just as with combinations.

(\begin{matrix} n \\ r \end{matrix}) = (\begin{matrix} n \\ n - r \end{matrix})

Find each binomial coefficient.

$(\begin{matrix} 7 \\ 3 \end{matrix})$
$(\begin{matrix} 11 \\ 4 \end{matrix})$

Using the Binomial Theorem

When we expand ${(x + y)}^{n}$

by multiplying, the result is called a binomial expansion, and it includes binomial coefficients. If we wanted to expand ${(x + y)}^{52},$

we might multiply $(x + y)$

by itself fifty-two times. This could take hours! If we examine some simple binomial expansions, we can find patterns that will lead us to a shortcut for finding more complicated binomial expansions.

\begin{array}{l} {(x + y)}^{2} = x^{2} + 2 x y + y^{2} \\ {(x + y)}^{3} = x^{3} + 3 x^{2} y + 3 x y^{2} + y^{3} \\ {(x + y)}^{4} = x^{4} + 4 x^{3} y + 6 x^{2} y^{2} + 4 x y^{3} + y^{4} \end{array}

First, let’s examine the exponents. With each successive term, the exponent for $x$

decreases and the exponent for $y$

increases. The sum of the two exponents is $n$

for each term.

Next, let’s examine the coefficients. Notice that the coefficients increase and then decrease in a symmetrical pattern. The coefficients follow a pattern:

(\begin{matrix} n \\ 0 \end{matrix}), (\begin{matrix} n \\ 1 \end{matrix}), (\begin{matrix} n \\ 2 \end{matrix}), ..., (\begin{matrix} n \\ n \end{matrix}) .

These patterns lead us to the Binomial Theorem, which can be used to expand any binomial.

\begin{array}{l} {(x + y)}^{n} & = \sum_{k = 0}^{n} (\begin{matrix} n \\ k \end{matrix}) x^{n - k} y^{k} \\ = x^{n} + (\begin{matrix} n \\ 1 \end{matrix}) x^{n - 1} y + (\begin{matrix} n \\ 2 \end{matrix}) x^{n - 2} y^{2} + ... + (\begin{matrix} n \\ n - 1 \end{matrix}) x y^{n - 1} + y^{n} \end{array}

Another way to see the coefficients is to examine the expansion of a binomial in general form, $x + y,$

to successive powers 1, 2, 3, and 4.

\begin{array}{l} {(x + y)}^{1} = x + y \\ {(x + y)}^{2} = x^{2} + 2 x y + y^{2} \\ {(x + y)}^{3} = x^{3} + 3 x^{2} y + 3 x y^{2} + y^{3} \\ {(x + y)}^{4} = x^{4} + 4 x^{3} y + 6 x^{2} y^{2} + 4 x y^{3} + y^{4} \end{array}

Can you guess the next expansion for the binomial ${(x + y)}^{5} ?$

Graph of the function f_2.

See [link], which illustrates the following:

There are $n + 1$
terms in the expansion of
${(x + y)}^{n} .$
The degree (or sum of the exponents) for each term is $n .$
The powers on $x$
begin with
$n$
and decrease to 0.
The powers on $y$
begin with 0 and increase to
$n .$
The coefficients are symmetric.

To determine the expansion on ${(x + y)}^{5},$

we see $n = 5,$

thus, there will be 5+1 = 6 terms. Each term has a combined degree of 5. In descending order for powers of $x,$

the pattern is as follows:

Introduce $x^{5},$
and then for each successive term reduce the exponent on
$x$
by 1 until
$x^{0} = 1$
is reached.
Introduce $y^{0} = 1,$
and then increase the exponent on
$y$
by 1 until
$y^{5}$
is reached.

$x^{5}, x^{4} y, x^{3} y^{2}, x^{2} y^{3}, x y^{4}, y^{5}$

The next expansion would be

{(x + y)}^{5} = x^{5} + 5 x^{4} y + 10 x^{3} y^{2} + 10 x^{2} y^{3} + 5 x y^{4} + y^{5} .

But where do those coefficients come from? The binomial coefficients are symmetric. We can see these coefficients in an array known as Pascal's Triangle, shown in [link].

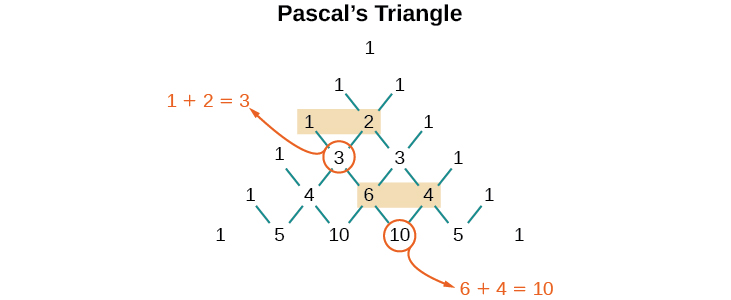
Pascal's Triangle

To generate Pascal’s Triangle, we start by writing a 1. In the row below, row 2, we write two 1’s. In the 3^rd row, flank the ends of the rows with 1’s, and add $1 + 1$

to find the middle number, 2. In the $n th$

row, flank the ends of the row with 1’s. Each element in the triangle is the sum of the two elements immediately above it.

To see the connection between Pascal’s Triangle and binomial coefficients, let us revisit the expansion of the binomials in general form.

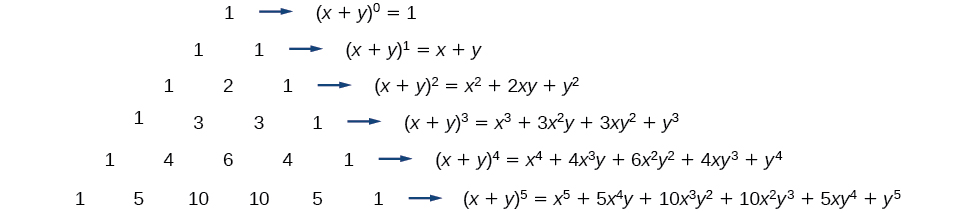Pascal's Triangle expanded to show the values of the triangle as x and y terms with exponents <div data-type="note" data-has-label="true" data-label="A General Note" markdown="1">

The Binomial Theorem

The Binomial Theorem is a formula that can be used to expand any binomial.

\begin{array}{l} {(x + y)}^{n} & = \sum_{k = 0}^{n} (\begin{matrix} n \\ k \end{matrix}) x^{n - k} y^{k} \\ = x^{n} + (\begin{matrix} n \\ 1 \end{matrix}) x^{n - 1} y + (\begin{matrix} n \\ 2 \end{matrix}) x^{n - 2} y^{2} + ... + (\begin{matrix} n \\ n - 1 \end{matrix}) x y^{n - 1} + y^{n} \end{array}

</div>

Given a binomial, write it in expanded form.

Determine the value of $n$
according to the exponent.
Evaluate the $k = 0$
through
$k = n$
using the Binomial Theorem formula.
Simplify.

Expanding a Binomial

Write in expanded form.

${(x + y)}^{5}$
${(3 x - y)}^{4}$

Substitute $n = 5$
into the formula. Evaluate the
$k = 0$
through
$k = 5$
terms. Simplify.

$\begin{array}{l} {(x + y)}^{5} & = (\begin{matrix} 5 \\ 0 \end{matrix}) x^{5} y^{0} + (\begin{matrix} 5 \\ 1 \end{matrix}) x^{4} y^{1} + (\begin{matrix} 5 \\ 2 \end{matrix}) x^{3} y^{2} + (\begin{matrix} 5 \\ 3 \end{matrix}) x^{2} y^{3} + (\begin{matrix} 5 \\ 4 \end{matrix}) x^{1} y^{4} + (\begin{matrix} 5 \\ 5 \end{matrix}) x^{0} y^{5} \\ {(x + y)}^{5} & = x^{5} + 5 x^{4} y + 10 x^{3} y^{2} + 10 x^{2} y^{3} + 5 x y^{4} + y^{5} \end{array}$
Substitute $n = 4$
into the formula. Evaluate the
$k = 0$
through
$k = 4$
terms. Notice that
$3 x$
is in the place that was occupied by
$x$
and that
$- y$
is in the place that was occupied by
$y .$
So we substitute them. Simplify.

$\begin{array}{l} {(3 x - y)}^{4} & = (\begin{matrix} 4 \\ 0 \end{matrix}) {(3 x)}^{4} {(- y)}^{0} + (\begin{matrix} 4 \\ 1 \end{matrix}) {(3 x)}^{3} {(- y)}^{1} + (\begin{matrix} 4 \\ 2 \end{matrix}) {(3 x)}^{2} {(- y)}^{2} + (\begin{matrix} 4 \\ 3 \end{matrix}) {(3 x)}^{1} {(- y)}^{3} + (\begin{matrix} 4 \\ 4 \end{matrix}) {(3 x)}^{0} {(- y)}^{4} \\ {(3 x - y)}^{4} & = 81 x^{4} - 108 x^{3} y + 54 x^{2} y^{2} - 12 x y^{3} + y^{4} \end{array}$

Analysis

Notice the alternating signs in part b. This happens because $(- y)$

raised to odd powers is negative, but $(- y)$

raised to even powers is positive. This will occur whenever the binomial contains a subtraction sign.

Write in expanded form.

${(x - y)}^{5}$
${(2 x + 5 y)}^{3}$

$x^{5} - 5 x^{4} y + 10 x^{3} y^{2} - 10 x^{2} y^{3} + 5 x y^{4} - y^{5}$
$8 x^{3} + 60 x^{2} y + 150 x y^{2} + 125 y^{3}$

Using the Binomial Theorem to Find a Single Term

Expanding a binomial with a high exponent such as ${(x + 2 y)}^{16}$

can be a lengthy process.

Sometimes we are interested only in a certain term of a binomial expansion. We do not need to fully expand a binomial to find a single specific term.

Note the pattern of coefficients in the expansion of ${(x + y)}^{5} .$

{(x + y)}^{5} = x^{5} + (\begin{matrix} 5 \\ 1 \end{matrix}) x^{4} y + (\begin{matrix} 5 \\ 2 \end{matrix}) x^{3} y^{2} + (\begin{matrix} 5 \\ 3 \end{matrix}) x^{2} y^{3} + (\begin{matrix} 5 \\ 4 \end{matrix}) x y^{4} + y^{5}

The second term is $(\begin{matrix} 5 \\ 1 \end{matrix}) x^{4} y .$

The third term is $(\begin{matrix} 5 \\ 2 \end{matrix}) x^{3} y^{2} .$

We can generalize this result.

(\begin{matrix} n \\ r \end{matrix}) x^{n - r} y^{r}

The (r+1)th Term of a Binomial Expansion

The $(r + 1) th$

term of the binomial expansion of ${(x + y)}^{n}$

is:

(\begin{matrix} n \\ r \end{matrix}) x^{n - r} y^{r}

Given a binomial, write a specific term without fully expanding.

Determine the value of $n$
according to the exponent.
Determine $(r + 1) .$
Determine $r .$
Replace $r$
in the formula for the
$(r + 1) th$
term of the binomial expansion.

Writing a Given Term of a Binomial Expansion

Find the tenth term of ${(x + 2 y)}^{16}$

without fully expanding the binomial.

Because we are looking for the tenth term, $r + 1 = 10,$

we will use $r = 9$

in our calculations.

(\begin{matrix} n \\ r \end{matrix}) x^{n - r} y^{r}

(\begin{matrix} 16 \\ 9 \end{matrix}) x^{16 - 9} {(2 y)}^{9} = 5, 857, 280 x^{7} y^{9}

Find the sixth term of ${(3 x - y)}^{9}$

without fully expanding the binomial.

- 10, 206 x^{4} y^{5}

Access these online resources for additional instruction and practice with binomial expansion.

Key Equations

Binomial Theorem

{(x + y)}^{n} = \sum_{k - 0}^{n} (\begin{matrix} n \\ k \end{matrix}) x^{n - k} y^{k}

(r + 1) t h

term of a binomial expansion

(\begin{matrix} n \\ r \end{matrix}) x^{n - r} y^{r}

Key Concepts

$(\begin{matrix} n \\ r \end{matrix})$
is called a binomial coefficient and is equal to
$C (n, r) .$
See [link].
The Binomial Theorem allows us to expand binomials without multiplying. See [link].
We can find a given term of a binomial expansion without fully expanding the binomial. See [link].

Section Exercises

Verbal

What is a binomial coefficient, and how it is calculated?

A binomial coefficient is an alternative way of denoting the combination $C (n, r).$

It is defined as $(\begin{matrix} n \\ r \end{matrix}) = C (n, r) = \frac{n!}{r! (n - r)!} .$

What role do binomial coefficients play in a binomial expansion? Are they restricted to any type of number?

What is the Binomial Theorem and what is its use?

The Binomial Theorem is defined as ${(x + y)}^{n} = \sum_{k = 0}^{n} (\begin{matrix} n \\ k \end{matrix}) x^{n - k} y^{k}$

and can be used to expand any binomial.

When is it an advantage to use the Binomial Theorem? Explain.

Algebraic

For the following exercises, evaluate the binomial coefficient.

(\begin{matrix} 6 \\ 2 \end{matrix})

(\begin{matrix} 5 \\ 3 \end{matrix})

(\begin{matrix} 7 \\ 4 \end{matrix})

(\begin{matrix} 9 \\ 7 \end{matrix})

(\begin{matrix} 10 \\ 9 \end{matrix})

(\begin{matrix} 25 \\ 11 \end{matrix})

(\begin{matrix} 17 \\ 6 \end{matrix})

12,376

(\begin{matrix} 200 \\ 199 \end{matrix})

For the following exercises, use the Binomial Theorem to expand each binomial.

{(4 a - b)}^{3}

64 a^{3} - 48 a^{2} b + 12 a b^{2} - b^{3}

{(5 a + 2)}^{3}

{(3 a + 2 b)}^{3}

27 a^{3} + 54 a^{2} b + 36 a b^{2} + 8 b^{3}

{(2 x + 3 y)}^{4}

{(4 x + 2 y)}^{5}

1024 x^{5} + 2560 x^{4} y + 2560 x^{3} y^{2} + 1280 x^{2} y^{3} + 320 x y^{4} + 32 y^{5}

{(3 x - 2 y)}^{4}

{(4 x - 3 y)}^{5}

1024 x^{5} - 3840 x^{4} y + 5760 x^{3} y^{2} - 4320 x^{2} y^{3} + 1620 x y^{4} - 243 y^{5}

{(\frac{1}{x} + 3 y)}^{5}

{(x^{- 1} + 2 y^{- 1})}^{4}

\frac{1}{x^{4}} + \frac{8}{x^{3} y} + \frac{24}{x^{2} y^{2}} + \frac{32}{x y^{3}} + \frac{16}{y^{4}}

{(\sqrt{x} - \sqrt{y})}^{5}

For the following exercises, use the Binomial Theorem to write the first three terms of each binomial.

{(a + b)}^{17}

a^{17} + 17 a^{16} b + 136 a^{15} b^{2}

{(x - 1)}^{18}

{(a - 2 b)}^{15}

a^{15} - 30 a^{14} b + 420 a^{13} b^{2}

{(x - 2 y)}^{8}

{(3 a + b)}^{20}

3, 486, 784, 401 a^{20} + 23, 245, 229, 340 a^{19} b + 73, 609, 892, 910 a^{18} b^{2}

{(2 a + 4 b)}^{7}

{(x^{3} - \sqrt{y})}^{8}

x^{24} - 8 x^{21} \sqrt{y} + 28 x^{18} y

For the following exercises, find the indicated term of each binomial without fully expanding the binomial.

The fourth term of ${(2 x - 3 y)}^{4}$

The fourth term of ${(3 x - 2 y)}^{5}$

- 720 x^{2} y^{3}

The third term of ${(6 x - 3 y)}^{7}$

The eighth term of ${(7 + 5 y)}^{14}$

220, 812, 466, 875, 000 y^{7}

The seventh term of ${(a + b)}^{11}$

The fifth term of ${(x - y)}^{7}$

35 x^{3} y^{4}

The tenth term of ${(x - 1)}^{12}$

The ninth term of ${(a - 3 b^{2})}^{11}$

1, 082, 565 a^{3} b^{16}

The fourth term of ${(x^{3} - \frac{1}{2})}^{10}$

The eighth term of ${(\frac{y}{2} + \frac{2}{x})}^{9}$

\frac{1152 y^{2}}{x^{7}}

Graphical

For the following exercises, use the Binomial Theorem to expand the binomial $f (x) = {(x + 3)}^{4} .$

Then find and graph each indicated sum on one set of axes.

Find and graph $f_{1} (x),$

such that $f_{1} (x)$

is the first term of the expansion.

Find and graph $f_{2} (x),$

such that $f_{2} (x)$

is the sum of the first two terms of the expansion.

f_{2} (x) = x^{4} + 12 x^{3}

Graph of the function f_2.

Find and graph $f_{3} (x),$

such that $f_{3} (x)$

is the sum of the first three terms of the expansion.

Find and graph $f_{4} (x),$

such that $f_{4} (x)$

is the sum of the first four terms of the expansion.

f_{4} (x) = x^{4} + 12 x^{3} + 54 x^{2} + 108 x

Graph of the function f_4.

Find and graph $f_{5} (x),$

such that $f_{5} (x)$

is the sum of the first five terms of the expansion.

Extensions

In the expansion of ${(5 x + 3 y)}^{n},$

each term has the form $(\begin{matrix} n \\ k \end{matrix}) a^{n - k} b^{k}, where k$

successively takes on the value $0, 1, 2, ..., n .$

If $(\begin{matrix} n \\ k \end{matrix}) = (\begin{matrix} 7 \\ 2 \end{matrix}),$

what is the corresponding term?

590, 625 x^{5} y^{2}

In the expansion of ${(a + b)}^{n},$

the coefficient of $a^{n - k} b^{k}$

is the same as the coefficient of which other term?

Consider the expansion of ${(x + b)}^{40} .$

What is the exponent of $b$

in the $k th$

term?

k - 1

Find $(\begin{matrix} n \\ k - 1 \end{matrix}) + (\begin{matrix} n \\ k \end{matrix})$

and write the answer as a binomial coefficient in the form $(\begin{matrix} n \\ k \end{matrix}) .$

Prove it. Hint: Use the fact that, for any integer $p,$

such that $p \geq 1, p! = p (p - 1)! .$

(\begin{matrix} n \\ k - 1 \end{matrix}) + (\begin{array}{l} n \\ k \end{array}) = (\begin{matrix} n + 1 \\ k \end{matrix});

Proof:

\begin{array}{l} (\begin{matrix} n \\ k - 1 \end{matrix}) + (\begin{array}{l} n \\ k \end{array}) \\ = \frac{n!}{k! (n - k)!} + \frac{n!}{(k - 1)! (n - (k - 1))!} \\ = \frac{n!}{k! (n - k)!} + \frac{n!}{(k - 1)! (n - k + 1)!} \\ = \frac{(n - k + 1) n!}{(n - k + 1) k! (n - k)!} + \frac{k n!}{k (k - 1)! (n - k + 1)!} \\ = \frac{(n - k + 1) n! + k n!}{k! (n - k + 1)!} \\ = \frac{(n + 1) n!}{k! ((n + 1) - k)!} \\ = \frac{(n + 1)!}{k! ((n + 1) - k)!} \\ = (\begin{matrix} n + 1 \\ k \end{matrix}) \end{array}

Which expression cannot be expanded using the Binomial Theorem? Explain.

$(x^{2} - 2 x + 1)$
${(\sqrt{a} + 4 \sqrt{a} - 5)}^{8}$
${(x^{3} + 2 y^{2} - z)}^{5}$
${(3 x^{2} - \sqrt{2 y^{3}})}^{12}$

The expression ${(x^{3} + 2 y^{2} - z)}^{5}$

cannot be expanded using the Binomial Theorem because it cannot be rewritten as a binomial.

Glossary

binomial coefficient: the number of ways to choose r objects from n objects where order does not matter; equivalent to $C (n, r),$
denoted
$(\begin{matrix} n \\ r \end{matrix})$

binomial expansion: the result of expanding ${(x + y)}^{n}$
by multiplying

Binomial Theorem: a formula that can be used to expand any binomial

This work is licensed under a Creative Commons Attribution 4.0 International License.

You can also download for free at http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1

Attribution:

For questions regarding this license, please contact partners@openstaxcollege.org.
If you use this textbook as a bibliographic reference, then you should cite it as follows: OpenStax College, Algebra and Trigonometry. OpenStax CNX. http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1.
If you redistribute this textbook in a print format, then you must include on every physical page the following attribution: "Download for free at http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1."
If you redistribute part of this textbook, then you must retain in every digital format page view (including but not limited to EPUB, PDF, and HTML) and on every physical printed page the following attribution: "Download for free at http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1."