In this section, you will:
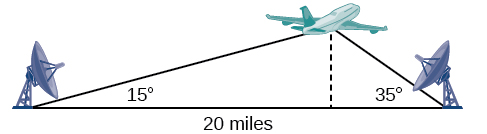
Suppose two radar stations located 20 miles apart each detect an aircraft between them. The angle of elevation measured by the first station is 35 degrees, whereas the angle of elevation measured by the second station is 15 degrees. How can we determine the altitude of the aircraft? We see in [link] that the triangle formed by the aircraft and the two stations is not a right triangle, so we cannot use what we know about right triangles. In this section, we will find out how to solve problems involving non-right triangles.

In any triangle, we can draw an altitude, a perpendicular line from one vertex to the opposite side, forming two right triangles. It would be preferable, however, to have methods that we can apply directly to non-right triangles without first having to create right triangles.
Any triangle that is not a right triangle is an oblique triangle. Solving an oblique triangle means finding the measurements of all three angles and all three sides. To do so, we need to start with at least three of these values, including at least one of the sides. We will investigate three possible oblique triangle problem situations:
ASA (angle-side-angle) We know the measurements of two angles and the included side. See [link]. 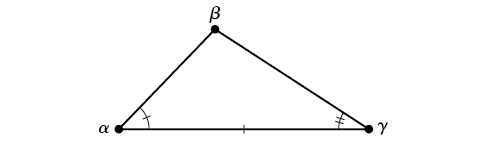
AAS (angle-angle-side) We know the measurements of two angles and a side that is not between the known angles. See [link]. 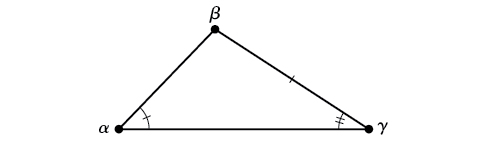
SSA (side-side-angle) We know the measurements of two sides and an angle that is not between the known sides. See [link]. 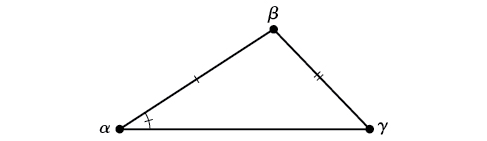
Knowing how to approach each of these situations enables us to solve oblique triangles without having to drop a perpendicular to form two right triangles. Instead, we can use the fact that the ratio of the measurement of one of the angles to the length of its opposite side will be equal to the other two ratios of angle measure to opposite side. Let’s see how this statement is derived by considering the triangle shown in [link].
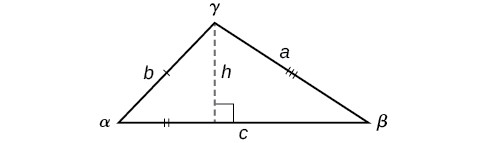
Using the right triangle relationships, we know that
and
Solving both equations for
gives two different expressions for
We then set the expressions equal to each other.
Similarly, we can compare the other ratios.
Collectively, these relationships are called the Law of Sines.
Note the standard way of labeling triangles: angle
(alpha) is opposite side
angle
(beta) is opposite side
and angle
(gamma) is opposite side
See [link].
While calculating angles and sides, be sure to carry the exact values through to the final answer. Generally, final answers are rounded to the nearest tenth, unless otherwise specified.
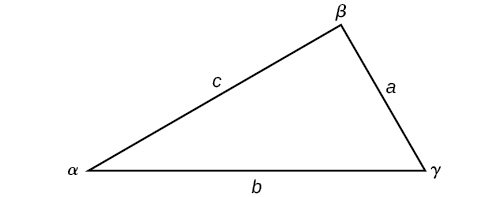
Given a triangle with angles and opposite sides labeled as in [link], the ratio of the measurement of an angle to the length of its opposite side will be equal to the other two ratios of angle measure to opposite side. All proportions will be equal. The Law of Sines is based on proportions and is presented symbolically two ways.
To solve an oblique triangle, use any pair of applicable ratios.
Solve the triangle shown in [link] to the nearest tenth.
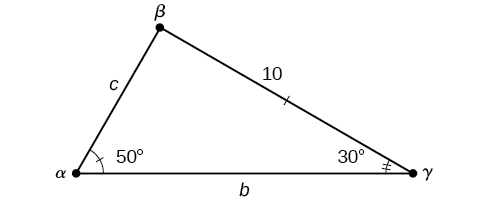
The three angles must add up to 180 degrees. From this, we can determine that
To find an unknown side, we need to know the corresponding angle and a known ratio. We know that angle
and its corresponding side
We can use the following proportion from the Law of Sines to find the length of
Similarly, to solve for
we set up another proportion.
Therefore, the complete set of angles and sides is
Solve the triangle shown in [link] to the nearest tenth.
We can use the Law of Sines to solve any oblique triangle, but some solutions may not be straightforward. In some cases, more than one triangle may satisfy the given criteria, which we describe as an ambiguous case. Triangles classified as SSA, those in which we know the lengths of two sides and the measurement of the angle opposite one of the given sides, may result in one or two solutions, or even no solution.
Oblique triangles in the category SSA may have four different outcomes. [link] illustrates the solutions with the known sides
and
and known angle
Solve the triangle in [link] for the missing side and find the missing angle measures to the nearest tenth.
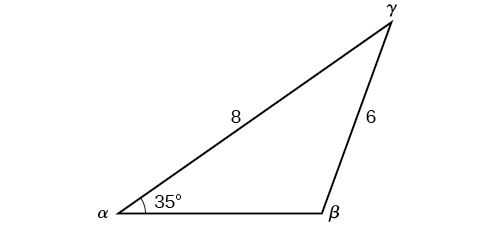
Use the Law of Sines to find angle
and angle
and then side
Solving for
we have the proportion
However, in the diagram, angle
appears to be an obtuse angle and may be greater than 90°. How did we get an acute angle, and how do we find the measurement of
Let’s investigate further. Dropping a perpendicular from
and viewing the triangle from a right angle perspective, we have [link]. It appears that there may be a second triangle that will fit the given criteria.
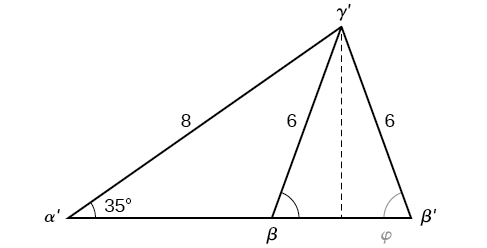
The angle supplementary to
is approximately equal to 49.9°, which means that
(Remember that the sine function is positive in both the first and second quadrants.) Solving for
we have
We can then use these measurements to solve the other triangle. Since
is supplementary to the sum of
and
we have
Now we need to find
and
We have
Finally,
To summarize, there are two triangles with an angle of 35°, an adjacent side of 8, and an opposite side of 6, as shown in [link].
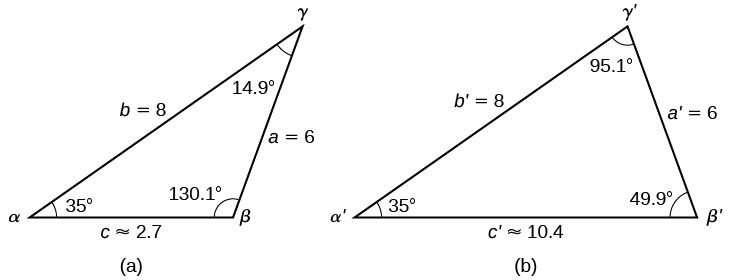
However, we were looking for the values for the triangle with an obtuse angle
We can see them in the first triangle (a) in [link].
Given
and
find the missing side and angles. If there is more than one possible solution, show both.
Solution 1
Solution 2
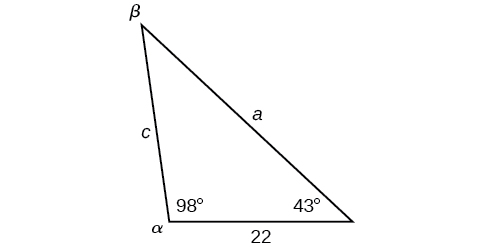
In the triangle shown in [link], solve for the unknown side and angles. Round your answers to the nearest tenth.
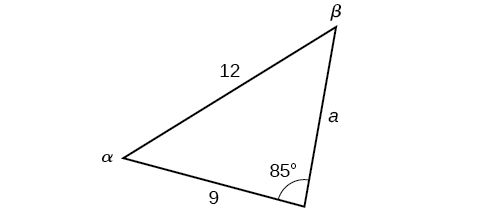
In choosing the pair of ratios from the Law of Sines to use, look at the information given. In this case, we know the angle
and its corresponding side
and we know side
We will use this proportion to solve for
To find
apply the inverse sine function. The inverse sine will produce a single result, but keep in mind that there may be two values for
It is important to verify the result, as there may be two viable solutions, only one solution (the usual case), or no solutions.
In this case, if we subtract
from 180°, we find that there may be a second possible solution. Thus,
To check the solution, subtract both angles, 131.7° and 85°, from 180°. This gives
which is impossible, and so
To find the remaining missing values, we calculate
Now, only side
is needed. Use the Law of Sines to solve for
by one of the proportions.
The complete set of solutions for the given triangle is
Given
find the missing side and angles. If there is more than one possible solution, show both. Round your answers to the nearest tenth.
Find all possible triangles if one side has length 4 opposite an angle of 50°, and a second side has length 10.
Using the given information, we can solve for the angle opposite the side of length 10. See [link].
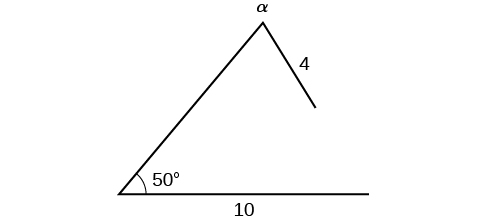
We can stop here without finding the value of
Because the range of the sine function is
it is impossible for the sine value to be 1.915. In fact, inputting
in a graphing calculator generates an ERROR DOMAIN. Therefore, no triangles can be drawn with the provided dimensions.
Determine the number of triangles possible given
two
Now that we can solve a triangle for missing values, we can use some of those values and the sine function to find the area of an oblique triangle. Recall that the area formula for a triangle is given as
where
is base and
is height. For oblique triangles, we must find
before we can use the area formula. Observing the two triangles in [link], one acute and one obtuse, we can drop a perpendicular to represent the height and then apply the trigonometric property
to write an equation for area in oblique triangles. In the acute triangle, we have
or
However, in the obtuse triangle, we drop the perpendicular outside the triangle and extend the base
to form a right triangle. The angle used in calculation is
or
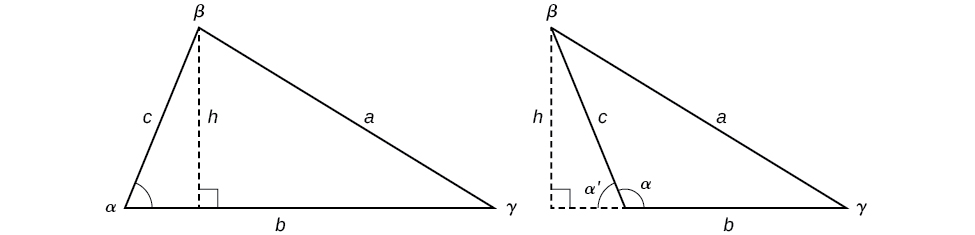
Thus,
Similarly,
The formula for the area of an oblique triangle is given by
This is equivalent to one-half of the product of two sides and the sine of their included angle.
Find the area of a triangle with sides
and angle
Round the area to the nearest integer.
Using the formula, we have
Find the area of the triangle given
Round the area to the nearest tenth.
about
The more we study trigonometric applications, the more we discover that the applications are countless. Some are flat, diagram-type situations, but many applications in calculus, engineering, and physics involve three dimensions and motion.
Find the altitude of the aircraft in the problem introduced at the beginning of this section, shown in [link]. Round the altitude to the nearest tenth of a mile.
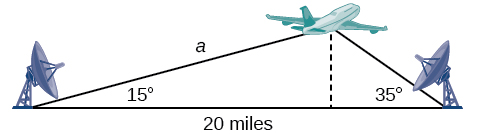
To find the elevation of the aircraft, we first find the distance from one station to the aircraft, such as the side
and then use right triangle relationships to find the height of the aircraft,
Because the angles in the triangle add up to 180 degrees, the unknown angle must be 180°−15°−35°=130°. This angle is opposite the side of length 20, allowing us to set up a Law of Sines relationship.
The distance from one station to the aircraft is about 14.98 miles.
Now that we know
we can use right triangle relationships to solve for
The aircraft is at an altitude of approximately 3.9 miles.
The diagram shown in [link] represents the height of a blimp flying over a football stadium. Find the height of the blimp if the angle of elevation at the southern end zone, point A, is 70°, the angle of elevation from the northern end zone, point
is 62°, and the distance between the viewing points of the two end zones is 145 yards.
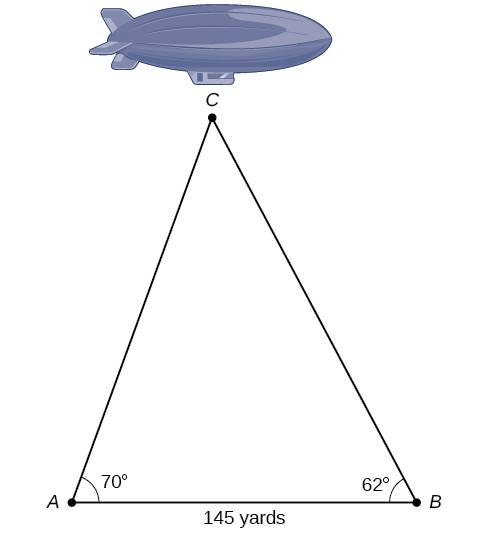
161.9 yd.
Access these online resources for additional instruction and practice with trigonometric applications.
| Law of Sines |
| Area for oblique triangles |
Describe the altitude of a triangle.
The altitude extends from any vertex to the opposite side or to the line containing the opposite side at a 90° angle.
Compare right triangles and oblique triangles.
When can you use the Law of Sines to find a missing angle?
When the known values are the side opposite the missing angle and another side and its opposite angle.
In the Law of Sines, what is the relationship between the angle in the numerator and the side in the denominator?
What type of triangle results in an ambiguous case?
A triangle with two given sides and a non-included angle.
For the following exercises, assume
is opposite side
is opposite side
and
is opposite side
Solve each triangle, if possible. Round each answer to the nearest tenth.
For the following exercises, use the Law of Sines to solve for the missing side for each oblique triangle. Round each answer to the nearest hundredth. Assume that angle
is opposite side
angle
is opposite side
and angle
is opposite side
Find side
when
Find side
when
Find side
when
For the following exercises, assume
is opposite side
is opposite side
and
is opposite side
Determine whether there is no triangle, one triangle, or two triangles. Then solve each triangle, if possible. Round each answer to the nearest tenth.
one triangle,
two triangles,
or
two triangles,
or
two triangles,
or
no triangle possible
For the following exercises, use the Law of Sines to solve, if possible, the missing side or angle for each triangle or triangles in the ambiguous case. Round each answer to the nearest tenth.
Find angle
when
Find angle
when
or
Find angle
when
For the following exercises, find the area of the triangle with the given measurements. Round each answer to the nearest tenth.
For the following exercises, find the length of side
Round to the nearest tenth.
For the following exercises, find the measure of angle
if possible. Round to the nearest tenth.
Notice that
is an obtuse angle.
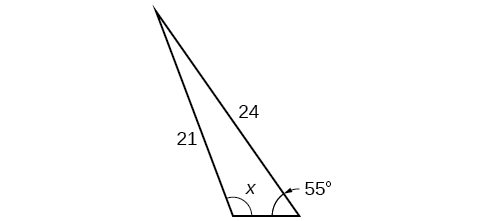
For the following exercises, find the area of each triangle. Round each answer to the nearest tenth.
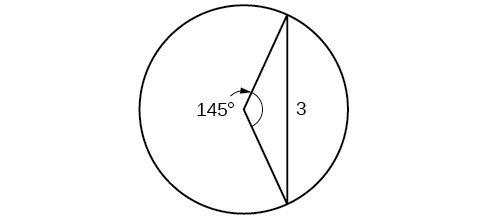
Find the radius of the circle in [link]. Round to the nearest tenth.
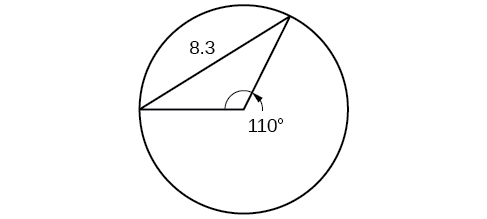
Find the diameter of the circle in [link]. Round to the nearest tenth.
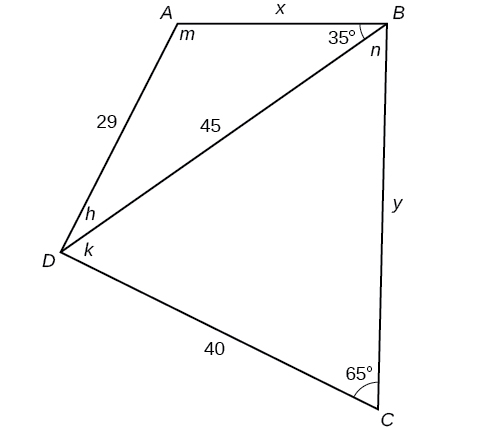
Solve both triangles in [link]. Round each answer to the nearest tenth.
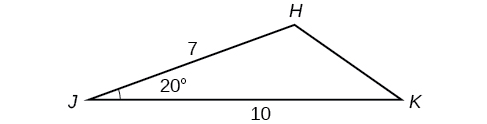
Solve the triangle in [link]. (Hint: Draw a perpendicular from
to
Round each answer to the nearest tenth.
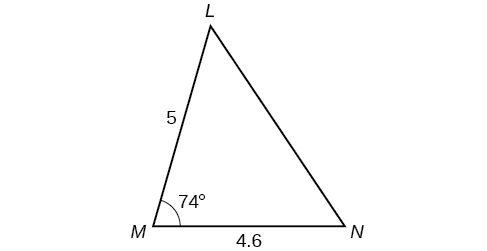
Solve the triangle in [link]. (Hint: Draw a perpendicular from
to
Round each answer to the nearest tenth.
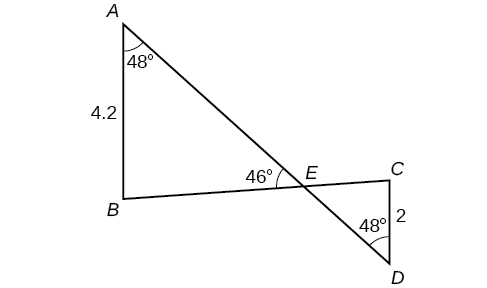
In [link],
is not a parallelogram.
is obtuse. Solve both triangles. Round each answer to the nearest tenth.
A pole leans away from the sun at an angle of
to the vertical, as shown in [link]. When the elevation of the sun is
the pole casts a shadow 42 feet long on the level ground. How long is the pole? Round the answer to the nearest tenth.
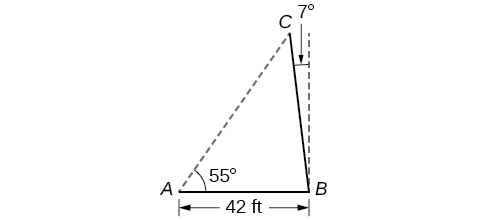
51.4 feet
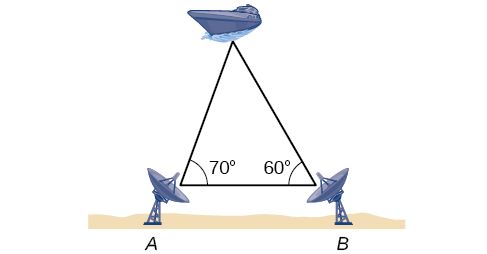
To determine how far a boat is from shore, two radar stations 500 feet apart find the angles out to the boat, as shown in [link]. Determine the distance of the boat from station
and the distance of the boat from shore. Round your answers to the nearest whole foot.
[link] shows a satellite orbiting Earth. The satellite passes directly over two tracking stations
and
which are 69 miles apart. When the satellite is on one side of the two stations, the angles of elevation at
and
are measured to be
and
respectively. How far is the satellite from station
and how high is the satellite above the ground? Round answers to the nearest whole mile.
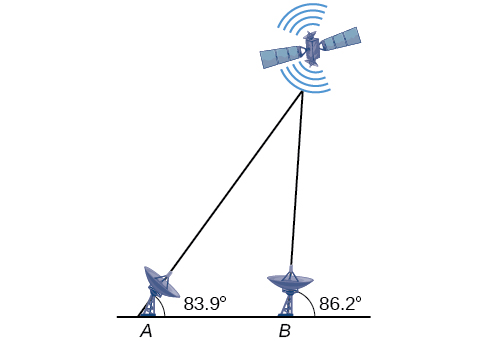
The distance from the satellite to station
is approximately 1716 miles. The satellite is approximately 1706 miles above the ground.
A communications tower is located at the top of a steep hill, as shown in [link]. The angle of inclination of the hill is
A guy wire is to be attached to the top of the tower and to the ground, 165 meters downhill from the base of the tower. The angle formed by the guy wire and the hill is
Find the length of the cable required for the guy wire to the nearest whole meter.
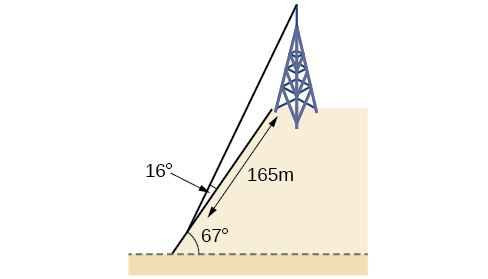
The roof of a house is at a
angle. An 8-foot solar panel is to be mounted on the roof and should be angled
relative to the horizontal for optimal results. (See [link]). How long does the vertical support holding up the back of the panel need to be? Round to the nearest tenth.
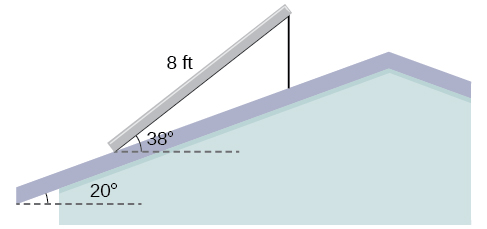
2.6 ft
Similar to an angle of elevation, an angle of depression is the acute angle formed by a horizontal line and an observer’s line of sight to an object below the horizontal. A pilot is flying over a straight highway. He determines the angles of depression to two mileposts, 6.6 km apart, to be
and
as shown in [link]. Find the distance of the plane from point
to the nearest tenth of a kilometer.
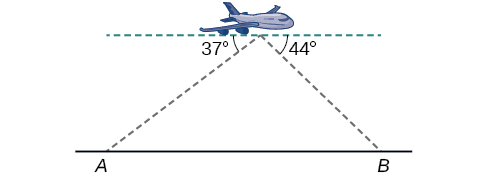
A pilot is flying over a straight highway. He determines the angles of depression to two mileposts, 4.3 km apart, to be 32° and 56°, as shown in [link]. Find the distance of the plane from point
to the nearest tenth of a kilometer.
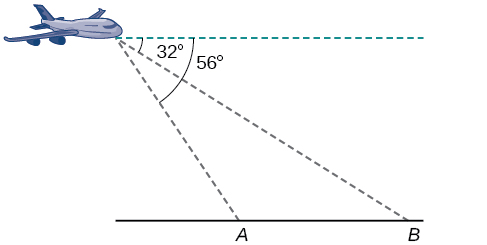
5.6 km
In order to estimate the height of a building, two students stand at a certain distance from the building at street level. From this point, they find the angle of elevation from the street to the top of the building to be 39°. They then move 300 feet closer to the building and find the angle of elevation to be 50°. Assuming that the street is level, estimate the height of the building to the nearest foot.
In order to estimate the height of a building, two students stand at a certain distance from the building at street level. From this point, they find the angle of elevation from the street to the top of the building to be 35°. They then move 250 feet closer to the building and find the angle of elevation to be 53°. Assuming that the street is level, estimate the height of the building to the nearest foot.
371 ft
Points
and
are on opposite sides of a lake. Point
is 97 meters from
The measure of angle
is determined to be 101°, and the measure of angle
is determined to be 53°. What is the distance from
to
rounded to the nearest whole meter?
A man and a woman standing
miles apart spot a hot air balloon at the same time. If the angle of elevation from the man to the balloon is 27°, and the angle of elevation from the woman to the balloon is 41°, find the altitude of the balloon to the nearest foot.
5936 ft
Two search teams spot a stranded climber on a mountain. The first search team is 0.5 miles from the second search team, and both teams are at an altitude of 1 mile. The angle of elevation from the first search team to the stranded climber is 15°. The angle of elevation from the second search team to the climber is 22°. What is the altitude of the climber? Round to the nearest tenth of a mile.
A street light is mounted on a pole. A 6-foot-tall man is standing on the street a short distance from the pole, casting a shadow. The angle of elevation from the tip of the man’s shadow to the top of his head of 28°. A 6-foot-tall woman is standing on the same street on the opposite side of the pole from the man. The angle of elevation from the tip of her shadow to the top of her head is 28°. If the man and woman are 20 feet apart, how far is the street light from the tip of the shadow of each person? Round the distance to the nearest tenth of a foot.
24.1 ft
Three cities,
and
are located so that city
is due east of city
If city
is located 35° west of north from city
and is 100 miles from city
and 70 miles from city
how far is city
from city
Round the distance to the nearest tenth of a mile.
Two streets meet at an 80° angle. At the corner, a park is being built in the shape of a triangle. Find the area of the park if, along one road, the park measures 180 feet, and along the other road, the park measures 215 feet.
19,056 ft2
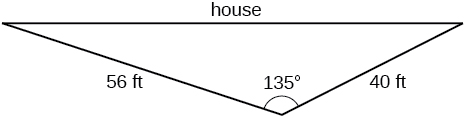
Brian’s house is on a corner lot. Find the area of the front yard if the edges measure 40 and 56 feet, as shown in [link].
The Bermuda triangle is a region of the Atlantic Ocean that connects Bermuda, Florida, and Puerto Rico. Find the area of the Bermuda triangle if the distance from Florida to Bermuda is 1030 miles, the distance from Puerto Rico to Bermuda is 980 miles, and the angle created by the two distances is 62°.
445,624 square miles
A yield sign measures 30 inches on all three sides. What is the area of the sign?
Naomi bought a modern dining table whose top is in the shape of a triangle. Find the area of the table top if two of the sides measure 4 feet and 4.5 feet, and the smaller angles measure 32° and 42°, as shown in [link].
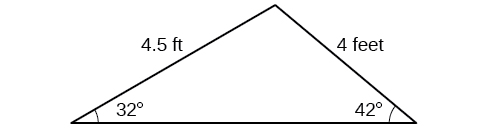
8.65 ft2

You can also download for free at http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1
Attribution: