
In this section, you will:
For any right triangle, given one other angle and the length of one side, we can figure out what the other angles and sides are. But what if we are given only two sides of a right triangle? We need a procedure that leads us from a ratio of sides to an angle. This is where the notion of an inverse to a trigonometric function comes into play. In this section, we will explore the inverse trigonometric functions.
In order to use inverse trigonometric functions, we need to understand that an inverse trigonometric function “undoes” what the original trigonometric function “does,” as is the case with any other function and its inverse. In other words, the domain of the inverse function is the range of the original function, and vice versa, as summarized in [link].

For example, if
then we would write
Be aware that
does not mean
The following examples illustrate the inverse trigonometric functions:
then
then
then
In previous sections, we evaluated the trigonometric functions at various angles, but at times we need to know what angle would yield a specific sine, cosine, or tangent value. For this, we need inverse functions. Recall that, for a one-to-one function, if
then an inverse function would satisfy
Bear in mind that the sine, cosine, and tangent functions are not one-to-one functions. The graph of each function would fail the horizontal line test. In fact, no periodic function can be one-to-one because each output in its range corresponds to at least one input in every period, and there are an infinite number of periods. As with other functions that are not one-to-one, we will need to restrict the domain of each function to yield a new function that is one-to-one. We choose a domain for each function that includes the number 0. [link] shows the graph of the sine function limited to
and the graph of the cosine function limited to
![(a) Sine function on a restricted domain of
[
−
π
2
,
π
2
];
(b) Cosine function on a restricted domain of
[
0,π
]
Two side-by-side graphs. The first graph, graph A, shows half of a period of the function sine of x. The second graph, graph B, shows half a period of the function cosine of x.](../resources/CNX_Precalc_Figure_06_03_001.jpg)
[link] shows the graph of the tangent function limited to
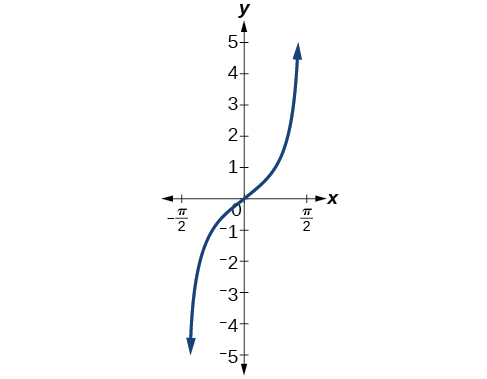
These conventional choices for the restricted domain are somewhat arbitrary, but they have important, helpful characteristics. Each domain includes the origin and some positive values, and most importantly, each results in a one-to-one function that is invertible. The conventional choice for the restricted domain of the tangent function also has the useful property that it extends from one vertical asymptote to the next instead of being divided into two parts by an asymptote.
On these restricted domains, we can define the inverse trigonometric functions.
means
The inverse sine function is sometimes called the arcsine function, and notated
means
The inverse cosine function is sometimes called the arccosine function, and notated
means
The inverse tangent function is sometimes called the arctangent function, and notated
The graphs of the inverse functions are shown in [link], [link], and [link]. Notice that the output of each of these inverse functions is a number, an angle in radian measure. We see that
has domain
and range
has domain
and range
and
has domain of all real numbers and range
To find the domain and range of inverse trigonometric functions, switch the domain and range of the original functions. Each graph of the inverse trigonometric function is a reflection of the graph of the original function about the line
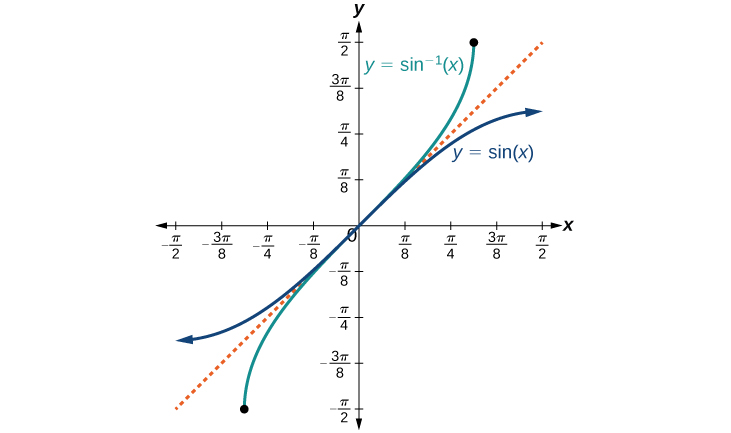
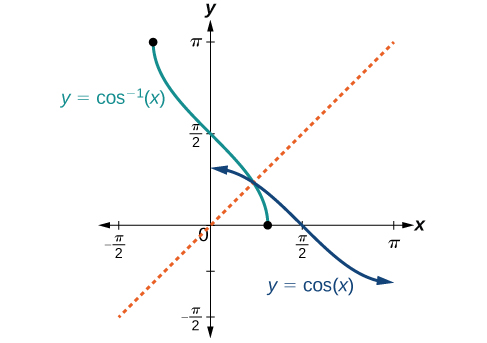
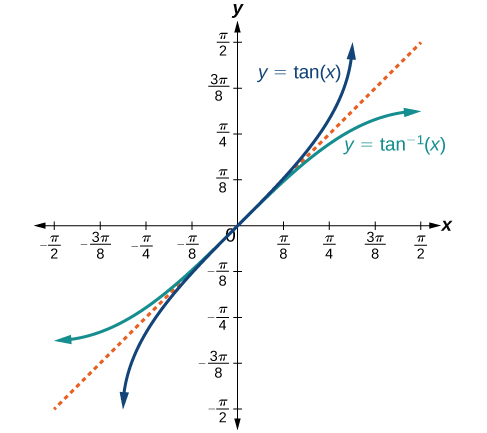
For angles in the interval
if
then
For angles in the interval
if
then
For angles in the interval
if
then
Given
write a relation involving the inverse sine.
Use the relation for the inverse sine. If
then
.
In this problem,
and
Given
write a relation involving the inverse cosine.
Now that we can identify inverse functions, we will learn to evaluate them. For most values in their domains, we must evaluate the inverse trigonometric functions by using a calculator, interpolating from a table, or using some other numerical technique. Just as we did with the original trigonometric functions, we can give exact values for the inverse functions when we are using the special angles, specifically
(30°),
(45°), and
(60°), and their reflections into other quadrants.
Given a “special” input value, evaluate an inverse trigonometric function.
for which the original trigonometric function has an output equal to the given input for the inverse trigonometric function.
is not in the defined range of the inverse, find another angle
that is in the defined range and has the same sine, cosine, or tangent as
depending on which corresponds to the given inverse function.
Evaluate each of the following.
is the same as determining the angle that would have a sine value of
In other words, what angle
would satisfy
There are multiple values that would satisfy this relationship, such as
and
but we know we need the angle in the interval
so the answer will be
Remember that the inverse is a function, so for each input, we will get exactly one output.
we know that
and
both have a sine value of
but neither is in the interval
For that, we need the negative angle coterminal with
we are looking for an angle in the interval
with a cosine value of
The angle that satisfies this is
we are looking for an angle in the interval
with a tangent value of 1. The correct angle is
Evaluate each of the following.
a.
b.
c.
d.
To evaluate inverse trigonometric functions that do not involve the special angles discussed previously, we will need to use a calculator or other type of technology. Most scientific calculators and calculator-emulating applications have specific keys or buttons for the inverse sine, cosine, and tangent functions. These may be labeled, for example, SIN
, ARCSIN, or ASIN.
In the previous chapter, we worked with trigonometry on a right triangle to solve for the sides of a triangle given one side and an additional angle. Using the inverse trigonometric functions, we can solve for the angles of a right triangle given two sides, and we can use a calculator to find the values to several decimal places.
In these examples and exercises, the answers will be interpreted as angles and we will use
as the independent variable. The value displayed on the calculator may be in degrees or radians, so be sure to set the mode appropriate to the application.
Evaluate
using a calculator.
Because the output of the inverse function is an angle, the calculator will give us a degree value if in degree mode and a radian value if in radian mode. Calculators also use the same domain restrictions on the angles as we are using.
In radian mode,
In degree mode,
Note that in calculus and beyond we will use radians in almost all cases.
Evaluate
using a calculator.
1.9823 or 113.578°
Given two sides of a right triangle like the one shown in [link], find an angle.

and the side of length
adjacent to the desired angle is given, use the equation
and the side of length
opposite to the desired angle is given, use the equation
Because we know the hypotenuse and the side adjacent to the angle, it makes sense for us to use the cosine function.
Solve the triangle in [link] for the angle
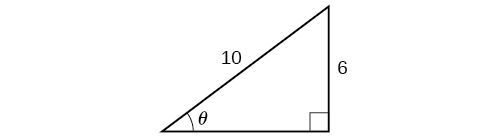
radians
There are times when we need to compose a trigonometric function with an inverse trigonometric function. In these cases, we can usually find exact values for the resulting expressions without resorting to a calculator. Even when the input to the composite function is a variable or an expression, we can often find an expression for the output. To help sort out different cases, let
and
be two different trigonometric functions belonging to the set
and let
and
be their inverses.
For any trigonometric function,
for all
in the proper domain for the given function. This follows from the definition of the inverse and from the fact that the range of
was defined to be identical to the domain of
However, we have to be a little more careful with expressions of the form
Is it correct that
</math> </strong>
No. This equation is correct ifbelongs to the restricted domainbut sine is defined for all real input values, and foroutside the restricted interval, the equation is not correct because its inverse always returns a value inThe situation is similar for cosine and tangent and their inverses. For example,
**Given an expression of the form f−1(f(θ)) where
evaluate.**
is in the restricted domain of
within the restricted domain of
such that
Then
Evaluate the following:
so
but
so
so
but
because cosine is an even function.
so
Evaluate
Now that we can compose a trigonometric function with its inverse, we can explore how to evaluate a composition of a trigonometric function and the inverse of another trigonometric function. We will begin with compositions of the form
For special values of
we can exactly evaluate the inner function and then the outer, inverse function. However, we can find a more general approach by considering the relation between the two acute angles of a right triangle where one is
making the other
Consider the sine and cosine of each angle of the right triangle in [link].
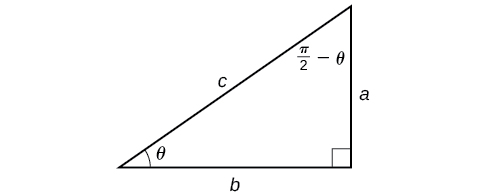
Because
we have
if
If
is not in this domain, then we need to find another angle that has the same cosine as
and does belong to the restricted domain; we then subtract this angle from
Similarly,
so
if
These are just the function-cofunction relationships presented in another way.
**Given functions of the form
and
evaluate them.**
then
then find another angle
such that
then
then find another angle
such that
Evaluate
Now, we can evaluate the inverse function as we did earlier.
and
Evaluate
To evaluate compositions of the form
where
and
are any two of the functions sine, cosine, or tangent and
is any input in the domain of
we have exact formulas, such as
When we need to use them, we can derive these formulas by using the trigonometric relations between the angles and sides of a right triangle, together with the use of Pythagoras’s relation between the lengths of the sides. We can use the Pythagorean identity,
to solve for one when given the other. We can also use the inverse trigonometric functions to find compositions involving algebraic expressions.
Find an exact value for
Beginning with the inside, we can say there is some angle such that
which means
and we are looking for
We can use the Pythagorean identity to do this.
Since
is in quadrant I,
must be positive, so the solution is
See [link].
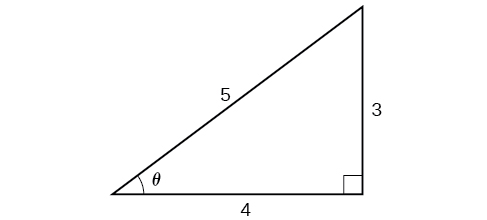
We know that the inverse cosine always gives an angle on the interval
so we know that the sine of that angle must be positive; therefore
Evaluate
Find an exact value for
While we could use a similar technique as in [link], we will demonstrate a different technique here. From the inside, we know there is an angle such that
We can envision this as the opposite and adjacent sides on a right triangle, as shown in [link].
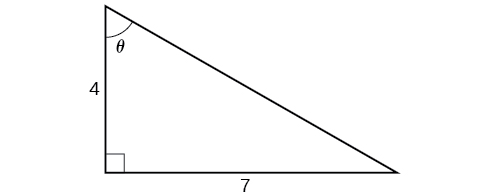
Using the Pythagorean Theorem, we can find the hypotenuse of this triangle.
Now, we can evaluate the sine of the angle as the opposite side divided by the hypotenuse.
This gives us our desired composition.
Evaluate
Find a simplified expression for
for
We know there is an angle
such that
Because we know that the inverse sine must give an angle on the interval
we can deduce that the cosine of that angle must be positive.
Find a simplified expression for
for
Access this online resource for additional instruction and practice with inverse trigonometric functions.
Visit this website for additional practice questions from Learningpod.
if
then
However,
only implies
if
is in the restricted domain of
See [link].
See [link].
See [link].
if
and
if
Why do the functions
and
have different ranges?
The function
is one-to-one on
thus, this interval is the range of the inverse function of
The function
is one-to-one on
thus, this interval is the range of the inverse function of
Since the functions
and
are inverse functions, why is
not equal to
Explain the meaning of
is the radian measure of an angle between
and
whose sine is 0.5.
Most calculators do not have a key to evaluate
Explain how this can be done using the cosine function or the inverse cosine function.
Why must the domain of the sine function,
be restricted to
for the inverse sine function to exist?
In order for any function to have an inverse, the function must be one-to-one and must pass the horizontal line test. The regular sine function is not one-to-one unless its domain is restricted in some way. Mathematicians have agreed to restrict the sine function to the interval
so that it is one-to-one and possesses an inverse.
Discuss why this statement is incorrect:
for all
Determine whether the following statement is true or false and explain your answer:
True . The angle,
that equals
,
, will be a second quadrant angle with reference angle,
, where
equals
,
. Since
is the reference angle for
,
and
=
-
For the following exercises, evaluate the expressions.
For the following exercises, use a calculator to evaluate each expression. Express answers to the nearest hundredth.
1.98
0.93
1.41
For the following exercises, find the angle
in the given right triangle. Round answers to the nearest hundredth.
0.56 radians
For the following exercises, find the exact value, if possible, without a calculator. If it is not possible, explain why.
0
0.71
-0.71
0.8
For the following exercises, find the exact value of the expression in terms of
with the help of a reference triangle.
For the following exercises, evaluate the expression without using a calculator. Give the exact value.
For the following exercises, find the function if
Graph
and state the domain and range of the function.
Graph
and state the domain and range of the function.
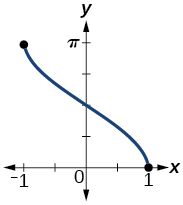 domain
domain
range
Graph one cycle of
and state the domain and range of the function.
For what value of
does
Use a graphing calculator to approximate the answer.
approximately
For what value of
does
Use a graphing calculator to approximate the answer.
Suppose a 13-foot ladder is leaning against a building, reaching to the bottom of a second-floor window 12 feet above the ground. What angle, in radians, does the ladder make with the building?
0.395 radians
Suppose you drive 0.6 miles on a road so that the vertical distance changes from 0 to 150 feet. What is the angle of elevation of the road?
An isosceles triangle has two congruent sides of length 9 inches. The remaining side has a length of 8 inches. Find the angle that a side of 9 inches makes with the 8-inch side.
1.11 radians
Without using a calculator, approximate the value of
Explain why your answer is reasonable.
A truss for the roof of a house is constructed from two identical right triangles. Each has a base of 12 feet and height of 4 feet. Find the measure of the acute angle adjacent to the 4-foot side.
1.25 radians
The line
passes through the origin in the x,y-plane. What is the measure of the angle that the line makes with the positive x-axis?
The line
passes through the origin in the x,y-plane. What is the measure of the angle that the line makes with the negative x-axis?
0.405 radians
What percentage grade should a road have if the angle of elevation of the road is 4 degrees? (The percentage grade is defined as the change in the altitude of the road over a 100-foot horizontal distance. For example a 5% grade means that the road rises 5 feet for every 100 feet of horizontal distance.)
A 20-foot ladder leans up against the side of a building so that the foot of the ladder is 10 feet from the base of the building. If specifications call for the ladder’s angle of elevation to be between 35 and 45 degrees, does the placement of this ladder satisfy safety specifications?
No. The angle the ladder makes with the horizontal is 60 degrees.
Suppose a 15-foot ladder leans against the side of a house so that the angle of elevation of the ladder is 42 degrees. How far is the foot of the ladder from the side of the house?
For the following exercises, graph the functions for two periods and determine the amplitude or stretching factor, period, midline equation, and asymptotes.
amplitude: 3; period:
midline:
no asymptotes* * *
![A graph of two periods of a function with a cosine parent function. The graph has a range of [0,6] graphed over -2pi to 2pi. Maximums as -pi and pi.](../resources/CNX_Precalc_Figure_06_03_206.jpg)
amplitude: 3; period:
midline:
no asymptotes* * *
![A graph of four periods of a function with a cosine parent function. Graphed from -4pi to 4pi. Range is [-3,3].](../resources/CNX_Precalc_Figure_06_03_208.jpg)
amplitude: 3; period:
midline:
no asymptotes* * *
![A graph of two periods of a sinusoidal function. Range is [-7,-1]. Maximums at -5pi/4 and 3pi/4.](../resources/CNX_Precalc_Figure_06_03_210.jpg)
amplitude: 6; period:
midline:
no asymptotes* * *
![A sinusoidal graph over two periods. Range is [-7,5], amplitude is 6, and period is 2pi/3.](../resources/CNX_Precalc_Figure_06_03_212.jpg)
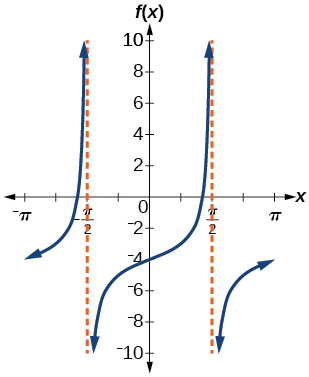
For the following exercises, graph the functions for two periods and determine the amplitude or stretching factor, period, midline equation, and asymptotes.
stretching factor: none; period:
midline:
asymptotes:
where
is an integer* * *
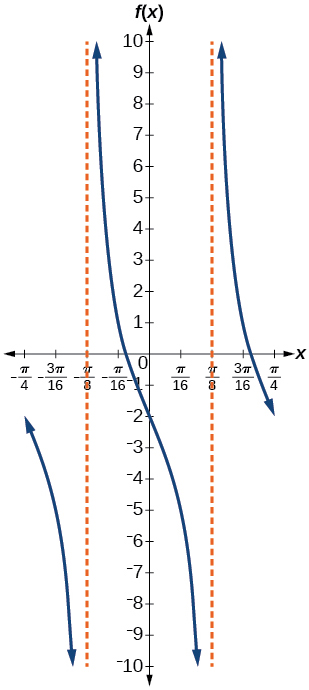
stretching factor: 3; period:
midline:
asymptotes:
where
is an integer* * *
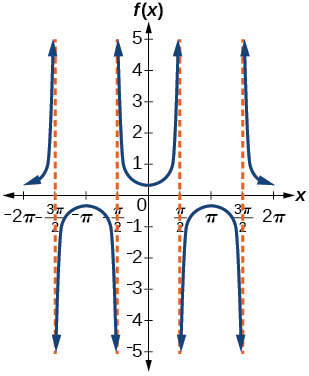
For the following exercises, graph two full periods. Identify the period, the phase shift, the amplitude, and asymptotes.
amplitude: none; period:
no phase shift; asymptotes:
where
is an odd integer* * *
amplitude: none; period:
no phase shift; asymptotes:
where
is an integer* * *
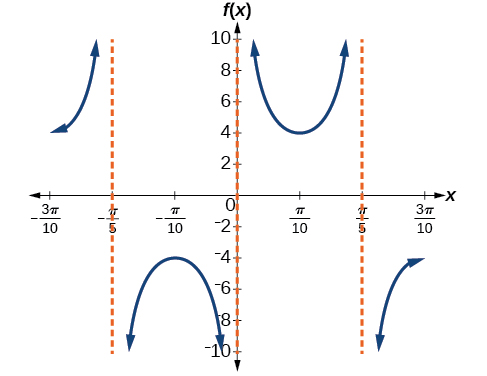
amplitude: none; period:
no phase shift; asymptotes:
where
is an integer* * *
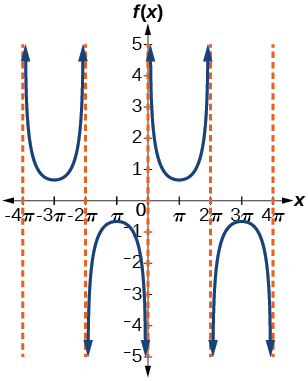
For the following exercises, use this scenario: The population of a city has risen and fallen over a 20-year interval. Its population may be modeled by the following function:
where the domain is the years since 1980 and the range is the population of the city.
What is the largest and smallest population the city may have?
largest: 20,000; smallest: 4,000
Graph the function on the domain of
.
What are the amplitude, period, and phase shift for the function?
amplitude: 8,000; period: 10; phase shift: 0
Over this domain, when does the population reach 18,000? 13,000?
What is the predicted population in 2007? 2010?
In 2007, the predicted population is 4,413. In 2010, the population will be 11,924.
For the following exercises, suppose a weight is attached to a spring and bobs up and down, exhibiting symmetry.
Suppose the graph of the displacement function is shown in [link], where the values on the x-axis represent the time in seconds and the y-axis represents the displacement in inches. Give the equation that models the vertical displacement of the weight on the spring.
![A graph of a consine function over one period. Graphed on the domain of [0,10]. Range is [-5,5].](../resources/CNX_Precalc_Figure_06_03_225.jpg)
At time = 0, what is the displacement of the weight?
5 in.
At what time does the displacement from the equilibrium point equal zero?
What is the time required for the weight to return to its initial height of 5 inches? In other words, what is the period for the displacement function?
10 seconds
For the following exercises, find the exact value without the aid of a calculator.
No solution
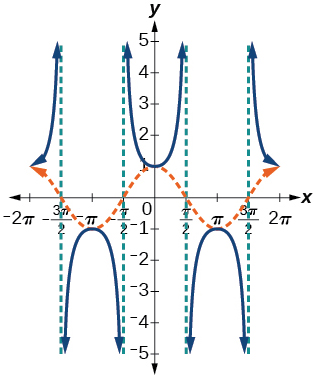
Graph
and
on the interval
and explain any observations.
The graphs are not symmetrical with respect to the line
They are symmetrical with respect to the
-axis.* * *
Graph
and
and explain any observations.
Graph the function
on the interval
and compare the graph to the graph of
on the same interval. Describe any observations.
The graphs appear to be identical.* * *
![Two graphs of two identical functions on the interval [-1 to 1]. Both graphs appear sinusoidal.](../resources/CNX_Precalc_Figure_06_03_228.jpg)
For the following exercises, sketch the graph of each function for two full periods. Determine the amplitude, the period, and the equation for the midline.
amplitude: 0.5; period:
midline
![A graph of two periods of a sinusoidal function, graphed over -2pi to 2pi. The range is [-0.5,0.5]. X-intercepts at multiples of pi.](../resources/CNX_Precalc_Figure_06_03_229.jpg)
amplitude: 5; period:
midline:
![Two periods of a sine function, graphed over -2pi to 2pi. The range is [-5,5], amplitude of 5, period of 2pi.](../resources/CNX_Precalc_Figure_06_03_231.jpg)
amplitude: 1; period:
midline:
![A graph of two periods of a cosine function, graphed over -7pi/3 to 5pi/3. Range is [0,2], Period is 2pi, amplitude is1.](../resources/CNX_Precalc_Figure_06_03_233.jpg)
amplitude: 3; period:
midline:
![A graph of two periods of a cosine function, over -7pi/2 to 17pi/2. The range is [-3,3], period is 6pi, and amplitude is 3.](../resources/CNX_Precalc_Figure_06_03_235.jpg)
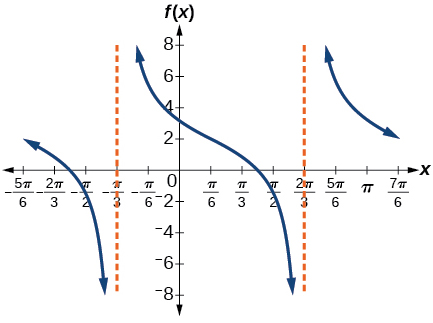
amplitude: none; period:
midline:
asymptotes:
where
is an integer* * *
amplitude: none; period:
midline:
asymptotes:
where
is an integer* * *
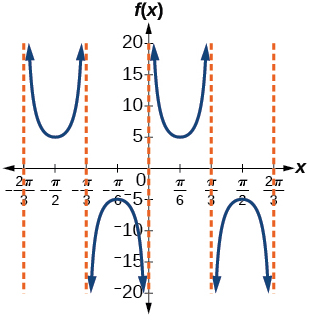
amplitude: none; period:
midline:
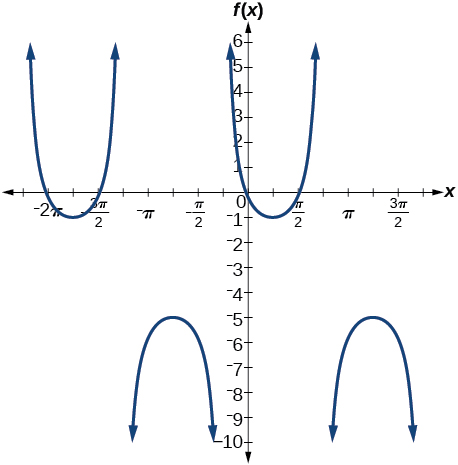
For the following exercises, determine the amplitude, period, and midline of the graph, and then find a formula for the function.
Give in terms of a sine function.* * *
![A graph of two periods of a sine function, graphed from -2 to 2. Range is [-6,-2], period is 2, and amplitude is 2.](../resources/CNX_Precalc_Figure_06_03_242.jpg)
Give in terms of a sine function.* * *
![A graph of two periods of a sine function, graphed over -2 to 2. Range is [-2,2], period is 2, and amplitude is 2.](../resources/CNX_Precalc_Figure_06_03_243.jpg)
amplitude: 2; period: 2; midline:
Give in terms of a tangent function.* * *
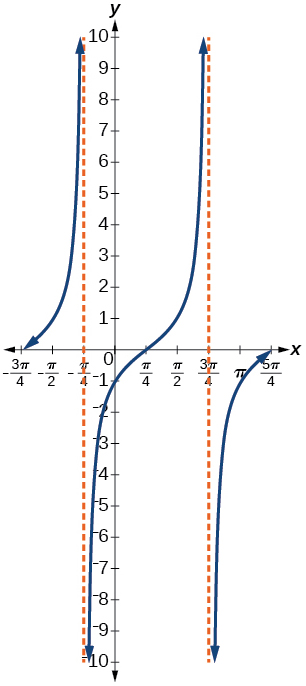
For the following exercises, find the amplitude, period, phase shift, and midline.
amplitude: 1; period: 12; phase shift:
midline
The outside temperature over the course of a day can be modeled as a sinusoidal function. Suppose you know the temperature is 68°F at midnight and the high and low temperatures during the day are 80°F and 56°F, respectively. Assuming
is the number of hours since midnight, find a function for the temperature,
in terms of
Water is pumped into a storage bin and empties according to a periodic rate. The depth of the water is 3 feet at its lowest at 2:00 a.m. and 71 feet at its highest, which occurs every 5 hours. Write a cosine function that models the depth of the water as a function of time, and then graph the function for one period.
For the following exercises, find the period and horizontal shift of each function.
period:
horizontal shift:
Write the equation for the graph in [link] in terms of the secant function and give the period and phase shift.
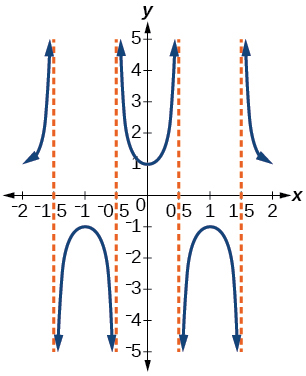
period: 2; phase shift: 0
If
find
If
find
For the following exercises, graph the functions on the specified window and answer the questions.
Graph
on the viewing window
by
Approximate the graph’s period.
Graph
on the following domains in
and
Suppose this function models sound waves. Why would these views look so different?
The views are different because the period of the wave is
Over a bigger domain, there will be more cycles of the graph.
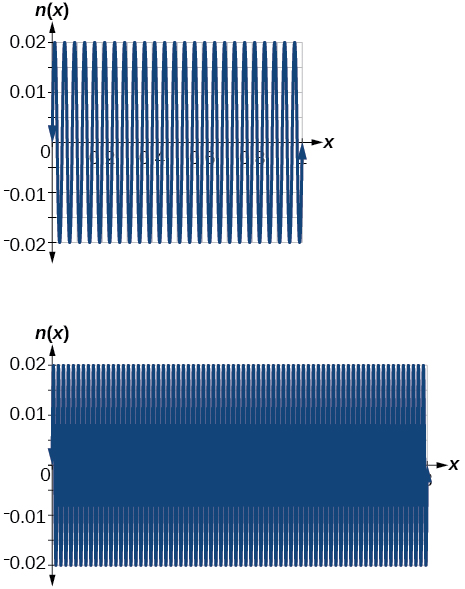
Graph
on
and explain any observations.
For the following exercises, let
What is the largest possible value for
What is the smallest possible value for
Where is the function increasing on the interval
On the approximate intervals
For the following exercises, find and graph one period of the periodic function with the given amplitude, period, and phase shift.
Sine curve with amplitude 3, period
and phase shift
Cosine curve with amplitude 2, period
and phase shift
![A graph of one period of a cosine function, graphed over -pi/4 to 0. Range is [1,5], period is pi/6.](../resources/CNX_Precalc_Figure_06_03_251.jpg)
For the following exercises, graph the function. Describe the graph and, wherever applicable, any periodic behavior, amplitude, asymptotes, or undefined points.
This graph is periodic with a period of
For the following exercises, find the exact value.
For the following exercises, suppose
Evaluate the following expressions.
For the following exercises, determine whether the equation is true or false.
False
The grade of a road is 7%. This means that for every horizontal distance of 100 feet on the road, the vertical rise is 7 feet. Find the angle the road makes with the horizontal in radians.
approximately 0.07 radians
which is the inverse of the cosine function and the angle that has a cosine equal to a given number
which is the inverse of the sine function and the angle that has a sine equal to a given number
which is the inverse of the tangent function and the angle that has a tangent equal to a given number

You can also download for free at http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1
Attribution: