
In this section, you will:
and
.

White light, such as the light from the sun, is not actually white at all. Instead, it is a composition of all the colors of the rainbow in the form of waves. The individual colors can be seen only when white light passes through an optical prism that separates the waves according to their wavelengths to form a rainbow.
Light waves can be represented graphically by the sine function. In the chapter on Trigonometric Functions, we examined trigonometric functions such as the sine function. In this section, we will interpret and create graphs of sine and cosine functions.
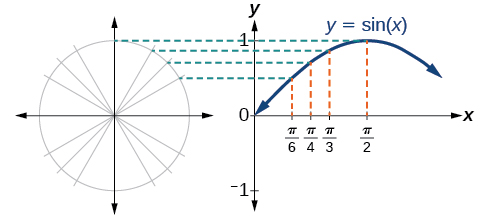
Recall that the sine and cosine functions relate real number values to the x- and y-coordinates of a point on the unit circle. So what do they look like on a graph on a coordinate plane? Let’s start with the sine function. We can create a table of values and use them to sketch a graph. [link] lists some of the values for the sine function on a unit circle.
|
</math></strong> |
| |
</math></strong> |
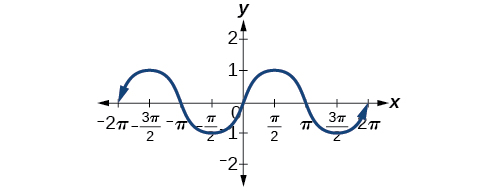
Plotting the points from the table and continuing along the x-axis gives the shape of the sine function. See [link].
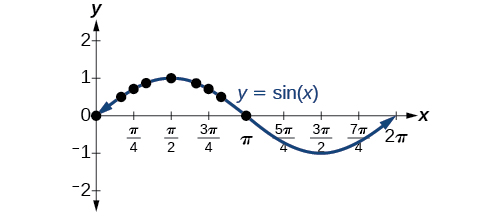
Notice how the sine values are positive between 0 and
which correspond to the values of the sine function in quadrants I and II on the unit circle, and the sine values are negative between
and
which correspond to the values of the sine function in quadrants III and IV on the unit circle. See [link].
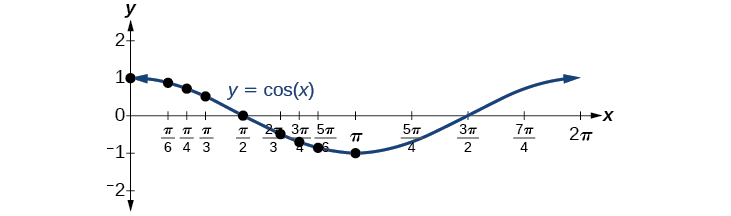
Now let’s take a similar look at the cosine function. Again, we can create a table of values and use them to sketch a graph. [link] lists some of the values for the cosine function on a unit circle.
As with the sine function, we can plots points to create a graph of the cosine function as in [link].
Because we can evaluate the sine and cosine of any real number, both of these functions are defined for all real numbers. By thinking of the sine and cosine values as coordinates of points on a unit circle, it becomes clear that the range of both functions must be the interval
In both graphs, the shape of the graph repeats after
which means the functions are periodic with a period of
A periodic function is a function for which a specific horizontal shift, P, results in a function equal to the original function:
for all values of
in the domain of
When this occurs, we call the smallest such horizontal shift with
the period of the function. [link] shows several periods of the sine and cosine functions.
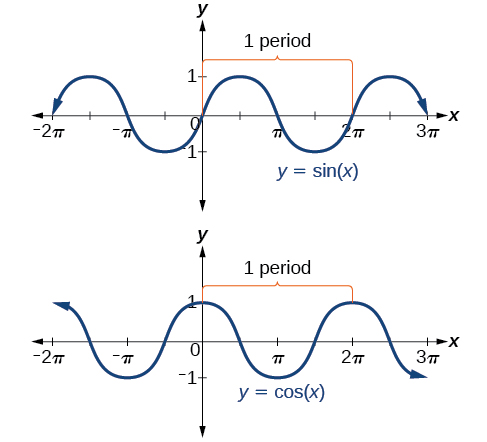
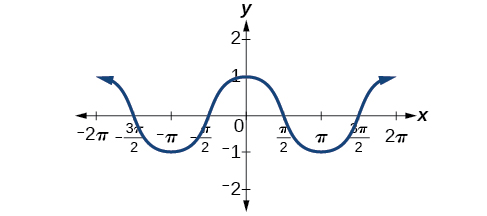
Looking again at the sine and cosine functions on a domain centered at the y-axis helps reveal symmetries. As we can see in [link], the sine function is symmetric about the origin. Recall from The Other Trigonometric Functions that we determined from the unit circle that the sine function is an odd function because
Now we can clearly see this property from the graph.
[link] shows that the cosine function is symmetric about the y-axis. Again, we determined that the cosine function is an even function. Now we can see from the graph that
The sine and cosine functions have several distinct characteristics:
and the range is
is symmetric about the origin, because it is an odd function.
is symmetric about the
axis, because it is an even function.
As we can see, sine and cosine functions have a regular period and range. If we watch ocean waves or ripples on a pond, we will see that they resemble the sine or cosine functions. However, they are not necessarily identical. Some are taller or longer than others. A function that has the same general shape as a sine or cosine function is known as a sinusoidal function. The general forms of sinusoidal functions are
Looking at the forms of sinusoidal functions, we can see that they are transformations of the sine and cosine functions. We can use what we know about transformations to determine the period.
In the general formula,
is related to the period by
If
then the period is less than
and the function undergoes a horizontal compression, whereas if
then the period is greater than
and the function undergoes a horizontal stretch. For example,
so the period is
which we knew. If
then
so the period is
and the graph is compressed. If
then
so the period is
and the graph is stretched. Notice in [link] how the period is indirectly related to
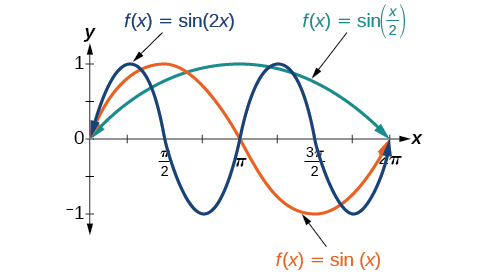
If we let
and
in the general form equations of the sine and cosine functions, we obtain the forms
The period is
Determine the period of the function
Let’s begin by comparing the equation to the general form
In the given equation,
so the period will be
Determine the period of the function
Returning to the general formula for a sinusoidal function, we have analyzed how the variable
relates to the period. Now let’s turn to the variable
so we can analyze how it is related to the amplitude, or greatest distance from rest.
represents the vertical stretch factor, and its absolute value
is the amplitude. The local maxima will be a distance
above the horizontal midline of the graph, which is the line
because
in this case, the midline is the x-axis. The local minima will be the same distance below the midline. If
the function is stretched. For example, the amplitude of
is twice the amplitude of
If
the function is compressed. [link] compares several sine functions with different amplitudes.
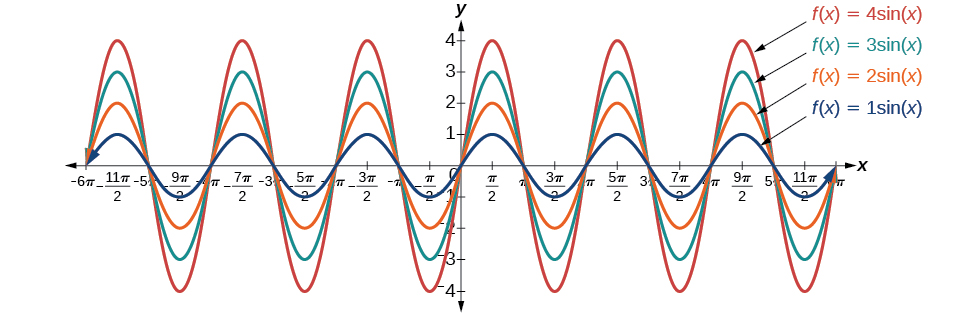
If we let
and
in the general form equations of the sine and cosine functions, we obtain the forms
The amplitude is
and the vertical height from the midline is
In addition, notice in the example that
What is the amplitude of the sinusoidal function
Is the function stretched or compressed vertically?
Let’s begin by comparing the function to the simplified form
In the given function,
so the amplitude is
The function is stretched.
The negative value of
results in a reflection across the x-axis of the sine function, as shown in [link].
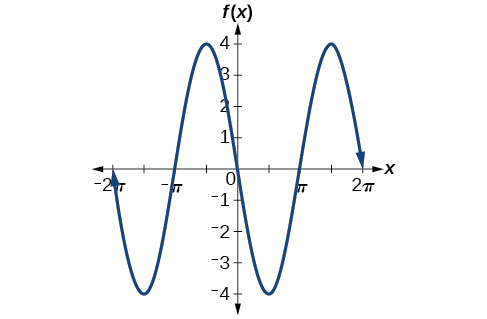
What is the amplitude of the sinusoidal function
Is the function stretched or compressed vertically?
compressed
Now that we understand how
and
relate to the general form equation for the sine and cosine functions, we will explore the variables
and
Recall the general form:
The value
for a sinusoidal function is called the phase shift, or the horizontal displacement of the basic sine or cosine function. If
the graph shifts to the right. If
the graph shifts to the left. The greater the value of
the more the graph is shifted. [link] shows that the graph of
shifts to the right by
units, which is more than we see in the graph of
which shifts to the right by
units.
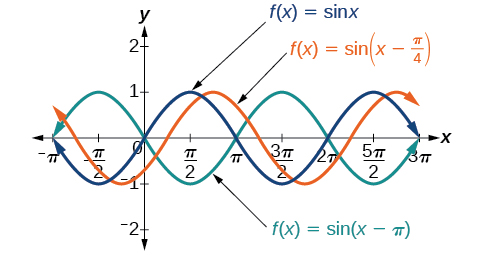
While
relates to the horizontal shift,
indicates the vertical shift from the midline in the general formula for a sinusoidal function. See [link]. The function
has its midline at
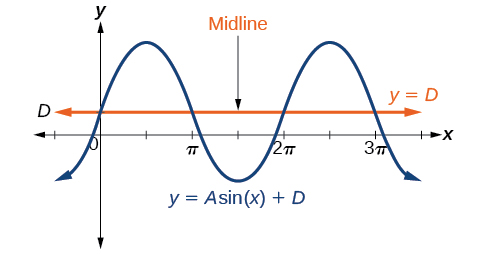
Any value of
other than zero shifts the graph up or down. [link] compares
with
which is shifted 2 units up on a graph.
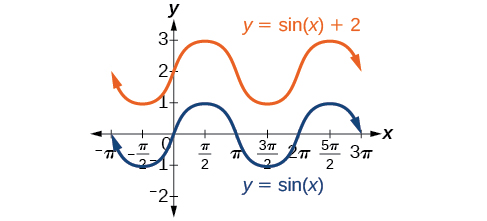
Given an equation in the form
or
is the phase shift and
is the vertical shift.
Determine the direction and magnitude of the phase shift for
Let’s begin by comparing the equation to the general form
In the given equation, notice that
and
So the phase shift is
or
units to the left.
We must pay attention to the sign in the equation for the general form of a sinusoidal function. The equation shows a minus sign before
Therefore
can be rewritten as
If the value of
is negative, the shift is to the left.
Determine the direction and magnitude of the phase shift for
right
Determine the direction and magnitude of the vertical shift for
Let’s begin by comparing the equation to the general form
In the given equation,
so the shift is 3 units downward.
Determine the direction and magnitude of the vertical shift for
2 units up
Given a sinusoidal function in the form
identify the midline, amplitude, period, and phase shift.
Determine the midline, amplitude, period, and phase shift of the function
Let’s begin by comparing the equation to the general form
so the amplitude is
Next,
so the period is
There is no added constant inside the parentheses, so
and the phase shift is
Finally,
so the midline is
Inspecting the graph, we can determine that the period is
the midline is
and the amplitude is 3. See [link].
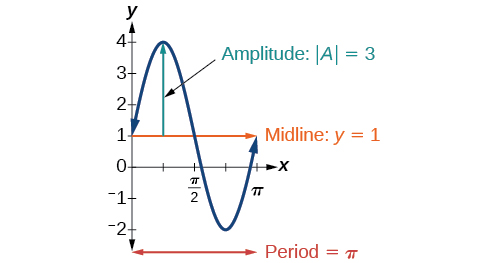
Determine the midline, amplitude, period, and phase shift of the function
midline:
amplitude:
period:
phase shift:
Determine the formula for the cosine function in [link].
![A graph of -0.5cos(x)+0.5. The graph has an amplitude of 0.5. The graph has a period of 2pi. The graph has a range of [0, 1]. The graph is also reflected about the x-axis from the parent function cos(x).](../resources/CNX_Precalc_Figure_06_01_015.jpg)
To determine the equation, we need to identify each value in the general form of a sinusoidal function.
The graph could represent either a sine or a cosine function that is shifted and/or reflected. When
the graph has an extreme point,
Since the cosine function has an extreme point for
let us write our equation in terms of a cosine function.
Let’s start with the midline. We can see that the graph rises and falls an equal distance above and below
This value, which is the midline, is
in the equation, so
The greatest distance above and below the midline is the amplitude. The maxima are 0.5 units above the midline and the minima are 0.5 units below the midline. So
Another way we could have determined the amplitude is by recognizing that the difference between the height of local maxima and minima is 1, so
Also, the graph is reflected about the x-axis so that
The graph is not horizontally stretched or compressed, so
and the graph is not shifted horizontally, so
Putting this all together,
Determine the formula for the sine function in [link].
![A graph of sin(x)+2. Period of 2pi, amplitude of 1, and range of [1, 3].](../resources/CNX_Precalc_Figure_06_01_016.jpg)
Determine the equation for the sinusoidal function in [link].
![A graph of 3cos(pi/3x-pi/3)-2. Graph has amplitude of 3, period of 6, range of [-5,1].](../resources/CNX_Precalc_Figure_06_01_017.jpg)
With the highest value at 1 and the lowest value at
the midline will be halfway between at
So
The distance from the midline to the highest or lowest value gives an amplitude of
The period of the graph is 6, which can be measured from the peak at
to the next peak at
or from the distance between the lowest points. Therefore,
Using the positive value for
we find that
So far, our equation is either
or
For the shape and shift, we have more than one option. We could write this as any one of the following:
While any of these would be correct, the cosine shifts are easier to work with than the sine shifts in this case because they involve integer values. So our function becomes
Again, these functions are equivalent, so both yield the same graph.
Write a formula for the function graphed in [link].
![A graph of 4sin((pi/5)x-pi/5)+4. Graph has period of 10, amplitude of 4, range of [0,8].](../resources/CNX_Precalc_Figure_06_01_018n.jpg)
two possibilities:
or
Throughout this section, we have learned about types of variations of sine and cosine functions and used that information to write equations from graphs. Now we can use the same information to create graphs from equations.
Instead of focusing on the general form equations
we will let
and
and work with a simplified form of the equations in the following examples.
**Given the function
sketch its graph.**
is positive or decreasing if
is negative.
there is a local maximum for
or a minimum for
with
(maximum for
) at
with
Sketch a graph of
Let’s begin by comparing the equation to the form
so the amplitude is 2.
so the period is
is negative, the graph descends as we move to the right of the origin.
the horizontal midpoints are at
and at the end of one period at
The quarter points include the minimum at
and the maximum at
A local minimum will occur 2 units below the midline, at
and a local maximum will occur at 2 units above the midline, at
[link] shows the graph of the function.
![A graph of -2sin((pi/2)x). Graph has range of [-2,2], period of 4, and amplitude of 2.](../resources/CNX_Precalc_Figure_06_01_019.jpg)
Sketch a graph of
Determine the midline, amplitude, period, and phase shift.
![A graph of -0.8cos(2x). Graph has range of [-0.8, 0.8], period of pi, amplitude of 0.8, and is reflected about the x-axis compared to it's parent function cos(x).](../resources/CNX_Precalc_Figure_06_01_020.jpg) midline:
midline:
amplitude:
period:
phase shift:
or none
Given a sinusoidal function with a phase shift and a vertical shift, sketch its graph.
shifted to the right or left by
and up or down by
Sketch a graph of
This graph will have the shape of a sine function, starting at the midline and increasing to the right.
The amplitude is 3.
we determine the period as follows.
The period is 8.
the phase shift is
The phase shift is 1 unit.
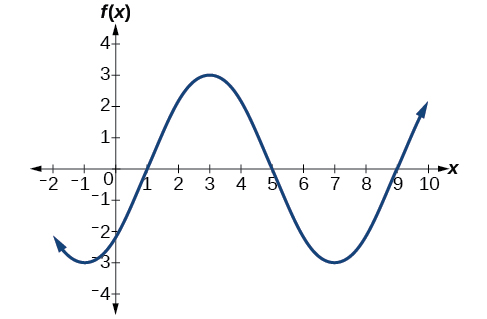
Draw a graph of
Determine the midline, amplitude, period, and phase shift.
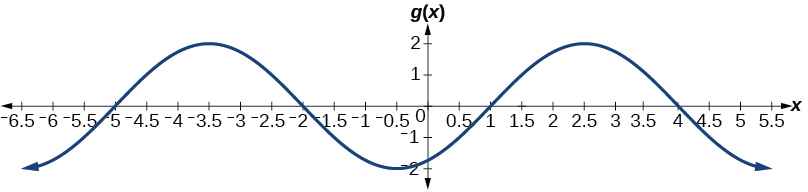 midline:
midline:
amplitude:
period:
phase shift:
Given
determine the amplitude, period, phase shift, and horizontal shift. Then graph the function.
Begin by comparing the equation to the general form and use the steps outlined in [link].
the amplitude is
so the period is
The period is 4.
so we calculate the phase shift as
The phase shift is
so the midline is
and the vertical shift is up 3.
Since
is negative, the graph of the cosine function has been reflected about the x-axis.
[link] shows one cycle of the graph of the function.
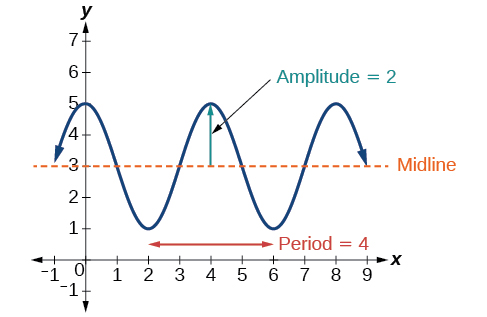
We can use the transformations of sine and cosine functions in numerous applications. As mentioned at the beginning of the chapter, circular motion can be modeled using either the sine or cosine function.
A point rotates around a circle of radius 3 centered at the origin. Sketch a graph of the y-coordinate of the point as a function of the angle of rotation.
Recall that, for a point on a circle of radius r, the y-coordinate of the point is
so in this case, we get the equation
The constant 3 causes a vertical stretch of the y-values of the function by a factor of 3, which we can see in the graph in [link].
![A graph of 3sin(x). Graph has period of 2pi, amplitude of 3, and range of [-3,3].](../resources/CNX_Precalc_Figure_06_01_023.jpg)
Notice that the period of the function is still
as we travel around the circle, we return to the point
for
Because the outputs of the graph will now oscillate between
and
the amplitude of the sine wave is
What is the amplitude of the function
Sketch a graph of this function.
7
![A graph of 7cos(x). Graph has amplitude of 7, period of 2pi, and range of [-7,7].](../resources/CNX_Precalc_Figure_06_01_024.jpg)
A circle with radius 3 ft is mounted with its center 4 ft off the ground. The point closest to the ground is labeled P, as shown in [link]. Sketch a graph of the height above the ground of the point
as the circle is rotated; then find a function that gives the height in terms of the angle of rotation.
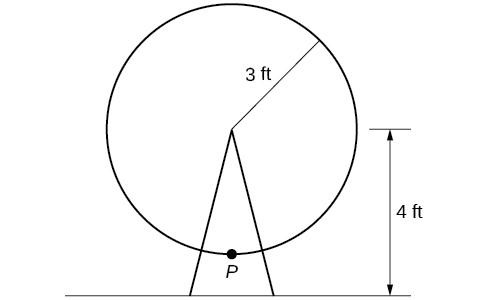
Sketching the height, we note that it will start 1 ft above the ground, then increase up to 7 ft above the ground, and continue to oscillate 3 ft above and below the center value of 4 ft, as shown in [link].
Although we could use a transformation of either the sine or cosine function, we start by looking for characteristics that would make one function easier to use than the other. Let’s use a cosine function because it starts at the highest or lowest value, while a sine function starts at the middle value. A standard cosine starts at the highest value, and this graph starts at the lowest value, so we need to incorporate a vertical reflection.
Second, we see that the graph oscillates 3 above and below the center, while a basic cosine has an amplitude of 1, so this graph has been vertically stretched by 3, as in the last example.
Finally, to move the center of the circle up to a height of 4, the graph has been vertically shifted up by 4. Putting these transformations together, we find that
A weight is attached to a spring that is then hung from a board, as shown in [link]. As the spring oscillates up and down, the position
of the weight relative to the board ranges from
in. (at time
to
in. (at time
below the board. Assume the position of
is given as a sinusoidal function of
Sketch a graph of the function, and then find a cosine function that gives the position
in terms of
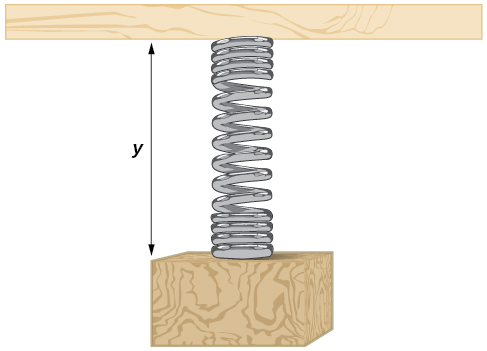
![A cosine graph with range [-1,-7]. Period is 2 pi. Local maximums at (0,-1), (2pi,-1), and (4pi, -1). Local minimums at (pi,-7) and (3pi, -7).](../resources/CNX_Precalc_Figure_06_01_027.jpg)
The London Eye is a huge Ferris wheel with a diameter of 135 meters (443 feet). It completes one rotation every 30 minutes. Riders board from a platform 2 meters above the ground. Express a rider’s height above ground as a function of time in minutes.
With a diameter of 135 m, the wheel has a radius of 67.5 m. The height will oscillate with amplitude 67.5 m above and below the center.
Passengers board 2 m above ground level, so the center of the wheel must be located
m above ground level. The midline of the oscillation will be at 69.5 m.
The wheel takes 30 minutes to complete 1 revolution, so the height will oscillate with a period of 30 minutes.
Lastly, because the rider boards at the lowest point, the height will start at the smallest value and increase, following the shape of a vertically reflected cosine curve.
so
so
so
An equation for the rider’s height would be
where
is in minutes and
is measured in meters.
Access these online resources for additional instruction and practice with graphs of sine and cosine functions.
| Sinusoidal functions |
is odd, so its graph is symmetric about the origin. The function
is even, so its graph is symmetric about the y-axis.
See [link].
represents amplitude. If
the function is stretched, whereas if
the function is compressed. See [link].
in the general formula for a sinusoidal function indicates the phase shift. See [link].
in the general formula for a sinusoidal function indicates the vertical shift from the midline. See [link].
Why are the sine and cosine functions called periodic functions?
The sine and cosine functions have the property that
for a certain
This means that the function values repeat for every
units on the x-axis.
How does the graph of
compare with the graph of
Explain how you could horizontally translate the graph of
to obtain
For the equation
what constants affect the range of the function and how do they affect the range?
The absolute value of the constant
(amplitude) increases the total range and the constant
(vertical shift) shifts the graph vertically.
How does the range of a translated sine function relate to the equation
How can the unit circle be used to construct the graph of
At the point where the terminal side of
intersects the unit circle, you can determine that the
equals the y-coordinate of the point.
For the following exercises, graph two full periods of each function and state the amplitude, period, and midline. State the maximum and minimum y-values and their corresponding x-values on one period for
Round answers to two decimal places if necessary.
![A graph of (2/3)cos(x). Graph has amplitude of 2/3, period of 2pi, and range of [-2/3, 2/3].](../resources/CNX_Precalc_Figure_06_01_202.jpg) amplitude:
amplitude:
period:
midline:
maximum:
occurs at
minimum:
occurs at
for one period, the graph starts at 0 and ends at
![A graph of 4sin(x). Graph has amplitude of 4, period of 2pi, and range of [-4, 4].](../resources/CNX_Precalc_Figure_06_01_204.jpg) amplitude: 4; period:
amplitude: 4; period:
midline:
maximum
occurs at
minimum:
occurs at
one full period occurs from
to
![A graph of cos(2x). Graph has amplitude of 1, period of pi, and range of [-1,1].](../resources/CNX_Precalc_Figure_06_01_206.jpg) amplitude: 1; period:
amplitude: 1; period:
midline:
maximum:
occurs at
minimum:
occurs at
one full period is graphed from
to
![A graph of 4cos(pi*x). Grpah has amplitude of 4, period of 2, and range of [-4, 4].](../resources/CNX_Precalc_Figure_06_01_208.jpg) amplitude: 4; period: 2; midline:
amplitude: 4; period: 2; midline:
maximum:
occurs at
minimum:
occurs at
![A graph of 3sin(8(x+4))+5. Graph has amplitude of 3, range of [2, 8], and period of pi/4.](../resources/CNX_Precalc_Figure_06_01_210.jpg) amplitude: 3; period:
amplitude: 3; period:
midline:
maximum:
occurs at
minimum:
occurs at
horizontal shift:
vertical translation 5; one period occurs from
to
![A graph of 5sin(5x+20)-2. Graph has an amplitude of 5, period of 2pi/5, and range of [-7,3].](../resources/CNX_Precalc_Figure_06_01_212.jpg) amplitude: 5; period:
amplitude: 5; period:
midline:
maximum:
occurs at
minimum:
occurs at
phase shift:
vertical translation:
one full period can be graphed on
to
For the following exercises, graph one full period of each function, starting at
For each function, state the amplitude, period, and midline. State the maximum and minimum y-values and their corresponding x-values on one period for
State the phase shift and vertical translation, if applicable. Round answers to two decimal places if necessary.
![A graph of -cos(t+pi/3)+1. Graph has amplitude of 1, period of 2pi, and range of [0,2]. Phase shifted pi/3 to the left.](../resources/CNX_Precalc_Figure_06_01_214.jpg) amplitude: 1 ; period:
amplitude: 1 ; period:
midline:
maximum:
occurs at
maximum:
occurs at
minimum:
occurs at
phase shift:
vertical translation: 1; one full period is from
to
![A graph of -sin((1/2)*t + 5pi/3). Graph has amplitude of 1, range of [-1,1], period of 4pi, and a phase shift of -10pi/3.](../resources/CNX_Precalc_Figure_06_01_216.jpg) amplitude: 1; period:
amplitude: 1; period:
midline:
maximum:
occurs at
minimum:
occurs at
phase shift:
vertical shift: 0
Determine the amplitude, midline, period, and an equation involving the sine function for the graph shown in [link].
![A sinusoidal graph with amplitude of 2, range of [-5, -1], period of 4, and midline at y=-3.](../resources/CNX_Precalc_Figure_06_01_218.jpg)
amplitude: 2; midline:
period: 4; equation:
Determine the amplitude, period, midline, and an equation involving cosine for the graph shown in [link].
![A graph with a cosine parent function, with amplitude of 3, period of pi, midline at y=-1, and range of [-4,2]](../resources/CNX_Precalc_Figure_06_01_219.jpg)
Determine the amplitude, period, midline, and an equation involving cosine for the graph shown in [link].
![A graph with a cosine parent function with an amplitude of 2, period of 5, midline at y=3, and a range of [1,5].](../resources/CNX_Precalc_Figure_06_01_220.jpg)
amplitude: 2; period: 5; midline:
equation:
Determine the amplitude, period, midline, and an equation involving sine for the graph shown in [link].
![A sinusoidal graph with amplitude of 4, period of 10, midline at y=0, and range [-4,4].](../resources/CNX_Precalc_Figure_06_01_221.jpg)
Determine the amplitude, period, midline, and an equation involving cosine for the graph shown in [link].
![A graph with cosine parent function, range of function is [-4,4], amplitude of 4, period of 2.](../resources/CNX_Precalc_Figure_06_01_222.jpg)
amplitude: 4; period: 2; midline:
equation:
Determine the amplitude, period, midline, and an equation involving sine for the graph shown in [link].
Determine the amplitude, period, midline, and an equation involving cosine for the graph shown in [link].
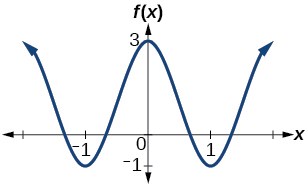
amplitude: 2; period: 2; midline
equation:
Determine the amplitude, period, midline, and an equation involving sine for the graph shown in [link].
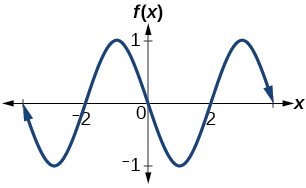
For the following exercises, let
On
solve
On
solve
Evaluate
On
Find all values of
On
the maximum value(s) of the function occur(s) at what x-value(s)?
On
the minimum value(s) of the function occur(s) at what x-value(s)?
Show that
This means that
is an odd function and possesses symmetry with respect to ________________.
For the following exercises, let
On
solve the equation
On
solve
On
find the x-intercepts of
On
find the x-values at which the function has a maximum or minimum value.
On
solve the equation
Graph
on
Explain why the graph appears as it does.
Graph
on
Did the graph appear as predicted in the previous exercise?
The graph appears linear. The linear functions dominate the shape of the graph for large values of
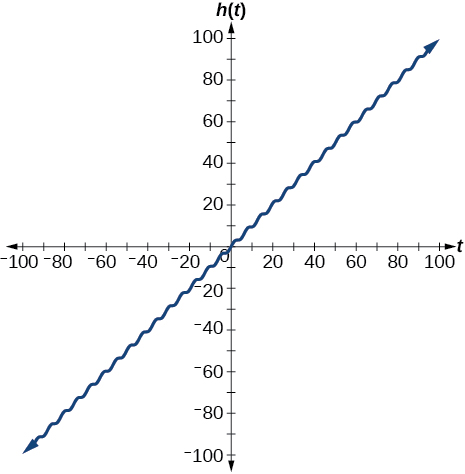
Graph
on
and verbalize how the graph varies from the graph of
Graph
on the window
and explain what the graph shows.
The graph is symmetric with respect to the y-axis and there is no amplitude because the function is not periodic.
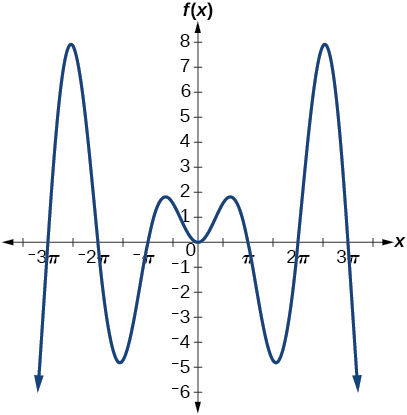
Graph
on the window
and explain what the graph shows.
A Ferris wheel is 25 meters in diameter and boarded from a platform that is 1 meter above the ground. The six o’clock position on the Ferris wheel is level with the loading platform. The wheel completes 1 full revolution in 10 minutes. The function
gives a person’s height in meters above the ground t minutes after the wheel begins to turn.
appearing in the definition of a sinusoidal function
where
appears in the general form of a sinusoidal function
that satisfies
for a specific constant
and any value of
or

You can also download for free at http://cnx.org/contents/13ac107a-f15f-49d2-97e8-60ab2e3b519c@11.1
Attribution: