 Once we see the graph, we can find the range of the function. The y-values of the function are greater than or equal to zero. The range then is
Once we see the graph, we can find the range of the function. The y-values of the function are greater than or equal to zero. The range then is By the end of this section, you will be able to:
Before you get started, take this readiness quiz.
In this section we will extend our previous work with functions to include radicals. If a function is defined by a radical expression, we call it a radical function.
The square root function is
The cube root function is
A radical function is a function that is defined by a radical expression.
To evaluate a radical function, we find the value of f(x) for a given value of x just as we did in our previous work with functions.
For the function
find ⓐ
ⓑ
ⓐ* * *
ⓑ* * *
Since the square root of a negative number is not a real number, the function does not have a value at
For the function
find ⓐ
ⓑ
ⓐ
ⓑ no value at
For the function
find ⓐ
ⓑ
ⓐ
ⓑ no value at
We follow the same procedure to evaluate cube roots.
For the function
find ⓐ
ⓑ
ⓐ* * *
ⓑ* * *
For the function
find ⓐ
ⓑ
ⓐ
ⓑ
For the function
find ⓐ
ⓑ
ⓐ
ⓑ
The next example has fourth roots.
For the function
find ⓐ
ⓑ
ⓐ* * *
ⓑ* * *
Since the fourth root of a negative number is not a real number, the function does not have a value at
For the function
find ⓐ
ⓑ
ⓐ
ⓑ
For the function
find ⓐ
ⓑ
ⓐ
ⓑ
To find the domain and range of radical functions, we use our properties of radicals. For a radical with an even index, we said the radicand had to be greater than or equal to zero as even roots of negative numbers are not real numbers. For an odd index, the radicand can be any real number. We restate the properties here for reference.
When n is an even number and:
then
is a real number.
then
is not a real number.
When n is an odd number,
is a real number for all values of a.
So, to find the domain of a radical function with even index, we set the radicand to be greater than or equal to zero. For an odd index radical, the radicand can be any real number.
When the index of the radical is even, the radicand must be greater than or equal to zero.
When the index of the radical is odd, the radicand can be any real number.
Find the domain of the function,
Write the domain in interval notation.
Since the function,
has a radical with an index of 2, which is even, we know the radicand must be greater than or equal to 0. We set the radicand to be greater than or equal to 0 and then solve to find the domain.
The domain of
is all values
and we write it in interval notation as
Find the domain of the function,
Write the domain in interval notation.
Find the domain of the function,
Write the domain in interval notation.
Find the domain of the function,
Write the domain in interval notation.
Since the function,
has a radical with an index of 2, which is even, we know the radicand must be greater than or equal to 0.
The radicand cannot be zero since the numerator is not zero.
For
to be greater than zero, the denominator must be positive since the numerator is positive. We know a positive divided by a positive is positive.
We set
and solve.
Also, since the radicand is a fraction, we must realize that the denominator cannot be zero.
We solve
to find the value that must be eliminated from the domain.
Putting this together we get the domain is
and we write it as
Find the domain of the function,
Write the domain in interval notation.
Find the domain of the function,
Write the domain in interval notation.
The next example involves a cube root and so will require different thinking.
Find the domain of the function,
Write the domain in interval notation.
Since the function,
has a radical with an index of 3, which is odd, we know the radicand can be any real number. This tells us the domain is any real number. In interval notation, we write
The domain of
is all real numbers and we write it in interval notation as
Find the domain of the function,
Write the domain in interval notation.
Find the domain of the function,
Write the domain in interval notation.
Before we graph any radical function, we first find the domain of the function. For the function,
the index is even, and so the radicand must be greater than or equal to 0.
This tells us the domain is
and we write this in interval notation as
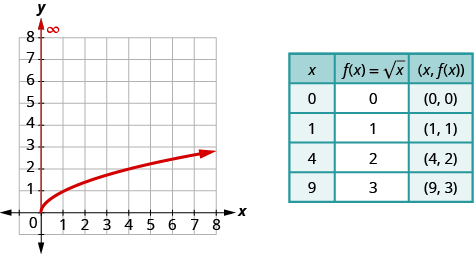
Previously we used point plotting to graph the function,
We chose x-values, substituted them in and then created a chart. Notice we chose points that are perfect squares in order to make taking the square root easier.
 Once we see the graph, we can find the range of the function. The y-values of the function are greater than or equal to zero. The range then is
Once we see the graph, we can find the range of the function. The y-values of the function are greater than or equal to zero. The range then is
For the function
ⓐ find the domain ⓑ graph the function ⓒ use the graph to determine the range.
ⓐ Since the radical has index 2, we know the radicand must be greater than or equal to zero. If
then
This tells us the domain is all values
and written in interval notation as
ⓑ To graph the function, we choose points in the interval
that will also give us a radicand which will be easy to take the square root.
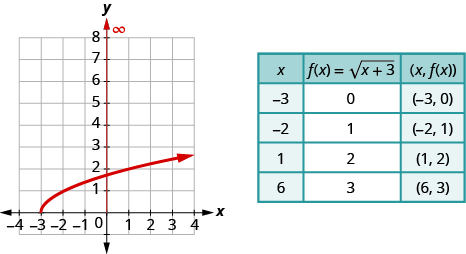 ⓒ Looking at the graph, we see the y-values of the function are greater than or equal to zero. The range then is
ⓒ Looking at the graph, we see the y-values of the function are greater than or equal to zero. The range then is
For the function
ⓐ find the domain ⓑ graph the function ⓒ use the graph to determine the range.
ⓐ domain:
ⓑ* * *
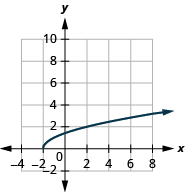
ⓒ range:
For the function
ⓐ find the domain ⓑ graph the function ⓒ use the graph to determine the range.
ⓐ domain:
ⓑ* * *
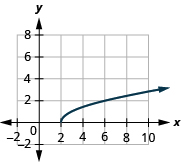
ⓒ range:
In our previous work graphing functions, we graphed
but we did not graph the function
We will do this now in the next example.
For the function
ⓐ find the domain ⓑ graph the function ⓒ use the graph to determine the range.
ⓐ Since the radical has index 3, we know the radicand can be any real number. This tells us the domain is all real numbers and written in interval notation as
ⓑ To graph the function, we choose points in the interval
that will also give us a radicand which will be easy to take the cube root.
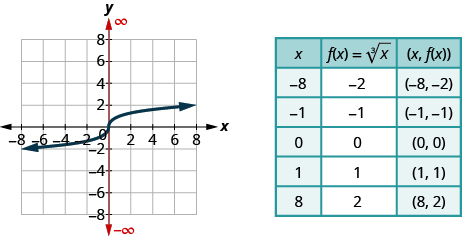 ⓒ Looking at the graph, we see the y-values of the function are all real numbers. The range then is
ⓒ Looking at the graph, we see the y-values of the function are all real numbers. The range then is
For the function
ⓐ find the domain ⓑ graph the function ⓒ use the graph to determine the range.
ⓐ domain:
ⓑ* * *
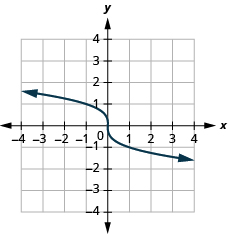
ⓒ range:
For the function
ⓐ find the domain ⓑ graph the function ⓒ use the graph to determine the range.
ⓐ domain:
ⓑ* * *
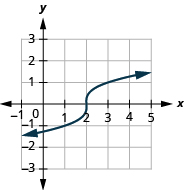
ⓒ range:
Access these online resources for additional instruction and practice with radical functions.
**Properties of
**
then
is a real number.
then
is not a real number.
is a real number for all values of a.
Domain of a Radical Function
Evaluate a Radical Function
In the following exercises, evaluate each function.
find* * *
ⓐ
ⓑ
ⓐ
ⓑ no value at
find* * *
ⓐ
ⓑ
find* * *
ⓐ
ⓑ
ⓐ
ⓑ
find* * *
ⓐ
ⓑ
find* * *
ⓐ
ⓑ
ⓐ
ⓑ
find* * *
ⓐ
ⓑ
find* * *
ⓐ
ⓑ
ⓐ
ⓑ
find* * *
ⓐ
ⓑ
find* * *
ⓐ
ⓑ
ⓐ
ⓑ
find* * *
ⓐ
ⓑ
find* * *
ⓐ
ⓑ
ⓐ
ⓑ
find* * *
ⓐ
ⓑ
For the function* * *
find* * *
ⓐ
ⓑ
ⓐ
ⓑ
For the function* * *
find* * *
ⓐ
ⓑ
For the function* * *
find* * *
ⓐ
ⓑ
ⓐ
ⓑ
For the function* * *
find* * *
ⓐ
ⓑ
Find the Domain of a Radical Function
In the following exercises, find the domain of the function and write the domain in interval notation.
Graph Radical Functions
In the following exercises, ⓐ find the domain of the function ⓑ graph the function ⓒ use the graph to determine the range.
ⓐ domain:
ⓑ* * *
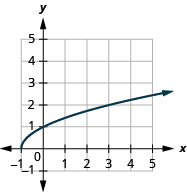
ⓒ
ⓐ domain:
ⓑ* * *
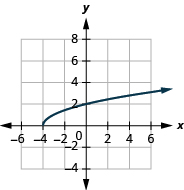
ⓒ
ⓐ domain:
ⓑ* * *
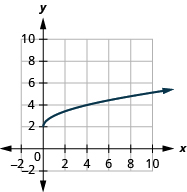
ⓒ
ⓐ domain:
ⓑ* * *
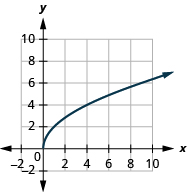
ⓒ
ⓐ domain:
ⓑ* * *
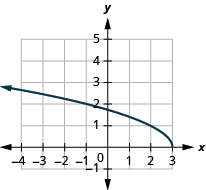
ⓒ
ⓐ domain:
ⓑ* * *
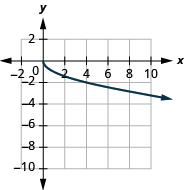
ⓒ
ⓐ domain:
ⓑ* * *
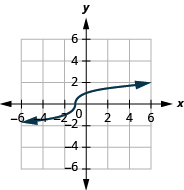
ⓒ
ⓐ domain:
ⓑ* * *
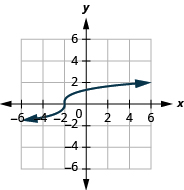
ⓒ
ⓐ domain:
ⓑ* * *
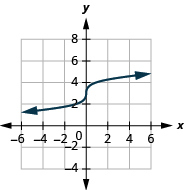
ⓒ
ⓐ domain:
ⓑ* * *
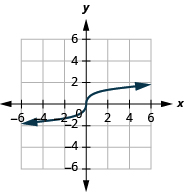
ⓒ
ⓐ domain:
ⓑ* * *
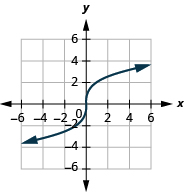
ⓒ
Explain how to find the domain of a fourth root function.
Answers will vary.
Explain how to find the domain of a fifth root function.
Explain why
is a function.
Answers will vary.
Explain why the process of finding the domain of a radical function with an even index is different from the process when the index is odd.
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
 ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?
ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?

You can also download for free at http://cnx.org/contents/02776133-d49d-49cb-bfaa-67c7f61b25a1@4.13
Attribution: