Rounding to three decimal places, approximate

|
|
| Use the Change-of-Base Formula. |
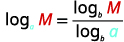
|
| Identify a and M. Choose 10 for b. |
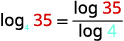
|
| Enter the expression in the calculator using the log button for base 10. Round to three decimal places. |
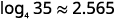
|
By the end of this section, you will be able to:
Before you get started, take this readiness quiz.
Now that we have learned about exponential and logarithmic functions, we can introduce some of the properties of logarithms. These will be very helpful as we continue to solve both exponential and logarithmic equations.
The first two properties derive from the definition of logarithms. Since
we can convert this to logarithmic form and get
Also, since
we get
In the next example we could evaluate the logarithm by converting to exponential form, as we have done previously, but recognizing and then applying the properties saves time.
Evaluate using the properties of logarithms: ⓐ
and ⓑ
ⓐ* * *
ⓑ* * *
Evaluate using the properties of logarithms: ⓐ
ⓑ
ⓐ 0 ⓑ 1
Evaluate using the properties of logarithms: ⓐ
ⓑ
ⓐ 0 ⓑ 1
The next two properties can also be verified by converting them from exponential form to logarithmic form, or the reverse.
The exponential equation
converts to the logarithmic equation
which is a true statement for positive values for x only.
The logarithmic equation
converts to the exponential equation
which is also a true statement.
These two properties are called inverse properties because, when we have the same base, raising to a power “undoes” the log and taking the log “undoes” raising to a power. These two properties show the composition of functions. Both ended up with the identity function which shows again that the exponential and logarithmic functions are inverse functions.
For
and
In the next example, apply the inverse properties of logarithms.
Evaluate using the properties of logarithms: ⓐ
and ⓑ
ⓐ* * *
ⓑ* * *
Evaluate using the properties of logarithms: ⓐ
ⓑ
ⓐ 15 ⓑ 4
Evaluate using the properties of logarithms: ⓐ
ⓑ
ⓐ 8 ⓑ 15
There are three more properties of logarithms that will be useful in our work. We know exponential functions and logarithmic function are very interrelated. Our definition of logarithm shows us that a logarithm is the exponent of the equivalent exponential. The properties of exponents have related properties for exponents.
In the Product Property of Exponents,
we see that to multiply the same base, we add the exponents. The Product Property of Logarithms,
tells us to take the log of a product, we add the log of the factors.
If
and
then,
The logarithm of a product is the sum of the logarithms.
We use this property to write the log of a product as a sum of the logs of each factor.
Use the Product Property of Logarithms to write each logarithm as a sum of logarithms. Simplify, if possible: ⓐ
and ⓑ
ⓐ* * *
ⓑ* * *
Use the Product Property of Logarithms to write each logarithm as a sum of logarithms. Simplify, if possible.
ⓐ
ⓑ
ⓐ
ⓑ
Use the Product Property of Logarithms to write each logarithm as a sum of logarithms. Simplify, if possible.
ⓐ
ⓑ
ⓐ
ⓑ
Similarly, in the Quotient Property of Exponents,
we see that to divide the same base, we subtract the exponents. The Quotient Property of Logarithms,
tells us to take the log of a quotient, we subtract the log of the numerator and denominator.
If
and
then,
The logarithm of a quotient is the difference of the logarithms.
Note that
We use this property to write the log of a quotient as a difference of the logs of each factor.
Use the Quotient Property of Logarithms to write each logarithm as a difference of logarithms. Simplify, if possible.* * *
ⓐ
and ⓑ
ⓐ* * *
ⓑ* * *
Use the Quotient Property of Logarithms to write each logarithm as a difference of logarithms. Simplify, if possible.
ⓐ
ⓑ
ⓐ
ⓑ
Use the Quotient Property of Logarithms to write each logarithm as a difference of logarithms. Simplify, if possible.
ⓐ
ⓑ
ⓐ
ⓑ
The third property of logarithms is related to the Power Property of Exponents,
we see that to raise a power to a power, we multiply the exponents. The Power Property of Logarithms,
tells us to take the log of a number raised to a power, we multiply the power times the log of the number.
If
and
is any real number then,
The log of a number raised to a power as the product product of the power times the log of the number.
We use this property to write the log of a number raised to a power as the product of the power times the log of the number. We essentially take the exponent and throw it in front of the logarithm.
Use the Power Property of Logarithms to write each logarithm as a product of logarithms. Simplify, if possible.* * *
ⓐ
and ⓑ
ⓐ* * *
ⓑ* * *
Use the Power Property of Logarithms to write each logarithm as a product of logarithms. Simplify, if possible.
ⓐ
ⓑ
ⓐ
ⓑ
Use the Power Property of Logarithms to write each logarithm as a product of logarithms. Simplify, if possible.
ⓐ
ⓑ
ⓐ
ⓑ
We summarize the Properties of Logarithms here for easy reference. While the natural logarithms are a special case of these properties, it is often helpful to also show the natural logarithm version of each property.
If
and
is any real number then,
| Property | Base |
| Base |
| {: valign=”top”} | ———- |
| {: valign=”top”} |
| {: valign=”top”} | Inverse Properties |
| {: valign=”top”} | Product Property of Logarithms |
| {: valign=”top”} | Quotient Property of Logarithms |
| {: valign=”top”} | Power Property of Logarithms |
| {: valign=”top”}{: .unnumbered summary=”.” data-label=””}
Now that we have the properties we can use them to “expand” a logarithmic expression. This means to write the logarithm as a sum or difference and without any powers.
We generally apply the Product and Quotient Properties before we apply the Power Property.
Use the Properties of Logarithms to expand the logarithm
. Simplify, if possible.
Use the Properties of Logarithms to expand the logarithm
. Simplify, if possible.
Use the Properties of Logarithms to expand the logarithm
. Simplify, if possible.
When we have a radical in the logarithmic expression, it is helpful to first write its radicand as a rational exponent.
Use the Properties of Logarithms to expand the logarithm
. Simplify, if possible.
Use the Properties of Logarithms to expand the logarithm
. Simplify, if possible.
Use the Properties of Logarithms to expand the logarithm
. Simplify, if possible.
The opposite of expanding a logarithm is to condense a sum or difference of logarithms that have the same base into a single logarithm. We again use the properties of logarithms to help us, but in reverse.
To condense logarithmic expressions with the same base into one logarithm, we start by using the Power Property to get the coefficients of the log terms to be one and then the Product and Quotient Properties as needed.
Use the Properties of Logarithms to condense the logarithm
. Simplify, if possible.
Use the Properties of Logarithms to condense the logarithm
. Simplify, if possible.
Use the Properties of Logarithms to condense the logarithm
. Simplify, if possible.
Use the Properties of Logarithms to condense the logarithm
. Simplify, if possible.
Use the Properties of Logarithms to condense the logarithm
. Simplify, if possible.
Use the Properties of Logarithms to condense the logarithm
. Simplify, if possible.
To evaluate a logarithm with any other base, we can use the Change-of-Base Formula. We will show how this is derived.
The Change-of-Base Formula introduces a new base
This can be any base b we want where
Because our calculators have keys for logarithms base 10 and base e, we will rewrite the Change-of-Base Formula with the new base as 10 or e.
For any logarithmic bases
and
When we use a calculator to find the logarithm value, we usually round to three decimal places. This gives us an approximate value and so we use the approximately equal symbol
.
Rounding to three decimal places, approximate

|
|
| Use the Change-of-Base Formula. |
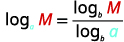
|
| Identify a and M. Choose 10 for b. |
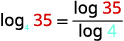
|
| Enter the expression in the calculator using the log button for base 10. Round to three decimal places. |
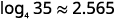
|
Rounding to three decimal places, approximate
Rounding to three decimal places, approximate
Access these online resources for additional instruction and practice with using the properties of logarithms.
and
and
then,
The logarithm of a product is the sum of the logarithms.
and
then,
The logarithm of a quotient is the difference of the logarithms.
and
is any real number then,
The log of a number raised to a power is the product of the power times the log of the number.
If
and
is any real number then,
| Property | Base |
| Base |
| Inverse Properties |
| Product Property of Logarithms |
| Quotient Property of Logarithms |
| Power Property of Logarithms |
For any logarithmic bases a and b, and
Use the Properties of Logarithms
In the following exercises, use the properties of logarithms to evaluate.
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ 0 ⓑ 1
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ 10 ⓑ 10
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ 15 ⓑ
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ 3 ⓑ 7
In the following exercises, use the Product Property of Logarithms to write each logarithm as a sum of logarithms. Simplify if possible.
In the following exercises, use the Quotient Property of Logarithms to write each logarithm as a sum of logarithms. Simplify if possible.
In the following exercises, use the Power Property of Logarithms to expand each. Simplify if possible.
In the following exercises, use the Properties of Logarithms to expand the logarithm. Simplify if possible.
In the following exercises, use the Properties of Logarithms to condense the logarithm. Simplify if possible.
2
2
0
Use the Change-of-Base Formula
In the following exercises, use the Change-of-Base Formula, rounding to three decimal places, to approximate each logarithm.
Write the Product Property in your own words. Does it apply to each of the following?
Why or why not?
Write the Power Property in your own words. Does it apply to each of the following?
Why or why not?
Answers will vary.
Use an example to show that* * *
Explain how to find the value of
using your calculator.
Answers will vary.
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
 ⓑ On a scale of
ⓑ On a scale of
how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?

You can also download for free at http://cnx.org/contents/02776133-d49d-49cb-bfaa-67c7f61b25a1@4.13
Attribution: