 To do a composition, the output of the first function,
To do a composition, the output of the first function, By the end of this section, you will be able to:
Before you get started, take this readiness quiz.
In this chapter, we will introduce two new types of functions, exponential functions and logarithmic functions. These functions are used extensively in business and the sciences as we will see.
Before we introduce the functions, we need to look at another operation on functions called composition. In composition, the output of one function is the input of a second function. For functions
and
the composition is written
and is defined by
We read
as
of
of
 To do a composition, the output of the first function,
To do a composition, the output of the first function,
becomes the input of the second function, f, and so we must be sure that it is part of the domain of f.
The composition of functions f and g is written
and is defined by
We read
as
of
of x.
We have actually used composition without using the notation many times before. When we graphed quadratic functions using translations, we were composing functions. For example, if we first graphed
as a parabola and then shifted it down vertically four units, we were using the composition defined by
where
 The next example will demonstrate that
The next example will demonstrate that
and
usually result in different outputs.
For functions
and
find: ⓐ
ⓑ
and ⓒ
ⓐ* * *
| Use the definition of |
| 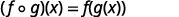 |
{: valign=”top”}|
|
{: valign=”top”}|  |
| 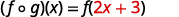 |
{: valign=”top”}|
|
{: valign=”top”}|  |
| 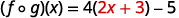 |
{: valign=”top”}| Distribute. |
|
{: valign=”top”}| Distribute. | 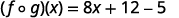 |
{: valign=”top”}| Simplify. |
|
{: valign=”top”}| Simplify. | 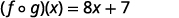 |
{: valign=”top”}{: .unnumbered .unstyled summary=”In the first step, we use the definition of f of g of x to obtain that f of g of x equals f of g of x. In the second step, we substitute 2 x plus 3 for g of x. This means that f of g of x equals f of 2 x plus 3. In the third step, we find f of 2 x plus 3 where f of x equals 4 x minus 5. This means that f of g of x equals 4 times the quantity 2 x plus 3, minus 5. In the fourth step, we distribute. This means that f of g of x equals 8 x plus 12 minus 5. In the fifth step, we simplify. This means that f of g of x equals 8 x plus 7.” data-label=””}
|
{: valign=”top”}{: .unnumbered .unstyled summary=”In the first step, we use the definition of f of g of x to obtain that f of g of x equals f of g of x. In the second step, we substitute 2 x plus 3 for g of x. This means that f of g of x equals f of 2 x plus 3. In the third step, we find f of 2 x plus 3 where f of x equals 4 x minus 5. This means that f of g of x equals 4 times the quantity 2 x plus 3, minus 5. In the fourth step, we distribute. This means that f of g of x equals 8 x plus 12 minus 5. In the fifth step, we simplify. This means that f of g of x equals 8 x plus 7.” data-label=””}
ⓑ* * *
| Use the definition of |
| 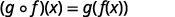 |
{: valign=”top”}|
|
{: valign=”top”}|  |
| 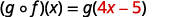 |
{: valign=”top”}|
|
{: valign=”top”}|  |
| 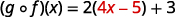 |
{: valign=”top”}| Distribute. |
|
{: valign=”top”}| Distribute. | 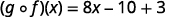 |
{: valign=”top”}| Simplify. |
|
{: valign=”top”}| Simplify. | 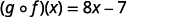 |
{: valign=”top”}{: .unnumbered .unstyled summary=”In the first step, we use the definition of g of f of x to obtain that g of f of x equals g of f of x. In the second step, we substitute 4 x minus 5 for f of x. This means that g of f of x equals g of 4 x minus 5. In the third step, we find g of 4 x minus 5 where g of x equals 2 x plus 3. This means that g of f of x equals 2 times the quantity 4 x minus 5, plus 3. In the fourth step, we distribute. This means that g of f of x equals 8 x minus 10 plus 3. In the fifth step, we simplify. This means that g of f of x equals 8 x minus 7.” data-label=””}
|
{: valign=”top”}{: .unnumbered .unstyled summary=”In the first step, we use the definition of g of f of x to obtain that g of f of x equals g of f of x. In the second step, we substitute 4 x minus 5 for f of x. This means that g of f of x equals g of 4 x minus 5. In the third step, we find g of 4 x minus 5 where g of x equals 2 x plus 3. This means that g of f of x equals 2 times the quantity 4 x minus 5, plus 3. In the fourth step, we distribute. This means that g of f of x equals 8 x minus 10 plus 3. In the fifth step, we simplify. This means that g of f of x equals 8 x minus 7.” data-label=””}
Notice the difference in the result in part ⓐ and part ⓑ.
ⓒ Notice that
is different than
In part ⓐ we did the composition of the functions. Now in part ⓒ we are not composing them, we are multiplying them.* * *
For functions
and
find ⓐ
ⓑ
ⓒ
.
ⓐ
ⓑ
ⓒ
For functions
and
find ⓐ
ⓑ
and ⓒ
ⓐ
ⓑ
ⓒ
In the next example we will evaluate a composition for a specific value.
For functions
and
find: ⓐ
ⓑ
and ⓒ
ⓐ* * *
| Use the definition of |
| 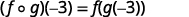 |
{: valign=”top”}|
|
{: valign=”top”}|  |
| 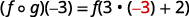 |
{: valign=”top”}| Simplify. |
|
{: valign=”top”}| Simplify. | 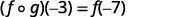 |
{: valign=”top”}|
|
{: valign=”top”}|  |
| 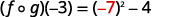 |
{: valign=”top”}| Simplify. |
|
{: valign=”top”}| Simplify. | 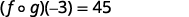 |
{: valign=”top”}{: .unnumbered .unstyled summary=”In the first step, we use the definition of f of g of negative 3 to obtain that f of g of negative 3 equals f evaluated at g of negative 3. In the second step, we find g of negative 3 where g of x equals 3 x plus 2. This means that f of g of negative 3 equals f evaluated at 3 times negative 3 plus 2. In the third step, we simplify to obtain that f of g of negative 3 equals f of negative 7. In the fourth step, we find f of negative 7 where f of x equals x squared minus 4. This means that f of g of negative 3 equals negative 7 squared minus 4. In the fifth step, we simplify to obtain that f of g of negative 3 equals 45.” data-label=””}
|
{: valign=”top”}{: .unnumbered .unstyled summary=”In the first step, we use the definition of f of g of negative 3 to obtain that f of g of negative 3 equals f evaluated at g of negative 3. In the second step, we find g of negative 3 where g of x equals 3 x plus 2. This means that f of g of negative 3 equals f evaluated at 3 times negative 3 plus 2. In the third step, we simplify to obtain that f of g of negative 3 equals f of negative 7. In the fourth step, we find f of negative 7 where f of x equals x squared minus 4. This means that f of g of negative 3 equals negative 7 squared minus 4. In the fifth step, we simplify to obtain that f of g of negative 3 equals 45.” data-label=””}
ⓑ* * *
| Use the definition of |
| 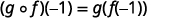 |
{: valign=”top”}|
|
{: valign=”top”}|  |
| 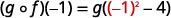 |
{: valign=”top”}| Simplify. |
|
{: valign=”top”}| Simplify. | 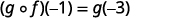 |
{: valign=”top”}|
|
{: valign=”top”}|  |
| 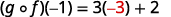 |
{: valign=”top”}| Simplify. |
|
{: valign=”top”}| Simplify. | 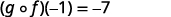 |
{: valign=”top”}{: .unnumbered .unstyled summary=”In the first step, we use the definition of g of f of negative 1 to obtain that g of f of negative 1 equals g evaluated at f of negative 1. In the second step, we find f of negative 1 where f of x equals x squared minus 4. This means that g of f of negative 1 equals g of negative 1 squared minus 4. In the third step, we simplify. This means that g of f of negative 1 equals g of negative 3. In the fourth step, we find g of negative 3 where g of x equals 3 x plus 2. This means that g of f of negative 1 equals 3 times negative 3 plus 2. In the fifth step, we simplify. This means that g of f of negative 1 equals negative 7.” data-label=””}
|
{: valign=”top”}{: .unnumbered .unstyled summary=”In the first step, we use the definition of g of f of negative 1 to obtain that g of f of negative 1 equals g evaluated at f of negative 1. In the second step, we find f of negative 1 where f of x equals x squared minus 4. This means that g of f of negative 1 equals g of negative 1 squared minus 4. In the third step, we simplify. This means that g of f of negative 1 equals g of negative 3. In the fourth step, we find g of negative 3 where g of x equals 3 x plus 2. This means that g of f of negative 1 equals 3 times negative 3 plus 2. In the fifth step, we simplify. This means that g of f of negative 1 equals negative 7.” data-label=””}
ⓒ* * *
| Use the definition of |
| 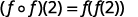 |
{: valign=”top”}|
|
{: valign=”top”}|  |
| 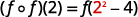 |
{: valign=”top”}| Simplify. |
|
{: valign=”top”}| Simplify. | 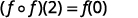 |
{: valign=”top”}|
|
{: valign=”top”}|  |
| 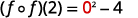 |
{: valign=”top”}| Simplify. |
|
{: valign=”top”}| Simplify. | 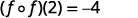 |
{: valign=”top”}{: .unnumbered .unstyled summary=”In the first step, we use the definition of f of f of 2 to obtain that f of f of 2 equals f evaluated at f of 2. In the second step, we find f of x where f of x equals x squared minus 4. This means that f of f of 2 equals f of 2 squared minus 4. In the third step, we simplify to obtain that f of f of 2 equals f of 0. In the fourth step, we find f of 0 where f of x equals x squared minus 4. This means that f of f of 2 equals 0 squared minus 4. In the fifth step, we simplify to obtain that f of f of 2 equals negative 4.” data-label=””}
|
{: valign=”top”}{: .unnumbered .unstyled summary=”In the first step, we use the definition of f of f of 2 to obtain that f of f of 2 equals f evaluated at f of 2. In the second step, we find f of x where f of x equals x squared minus 4. This means that f of f of 2 equals f of 2 squared minus 4. In the third step, we simplify to obtain that f of f of 2 equals f of 0. In the fourth step, we find f of 0 where f of x equals x squared minus 4. This means that f of f of 2 equals 0 squared minus 4. In the fifth step, we simplify to obtain that f of f of 2 equals negative 4.” data-label=””}
For functions
and
find ⓐ
ⓑ
and ⓒ
ⓐ –8 ⓑ 5 ⓒ 40
For functions
and
find ⓐ
ⓑ
and ⓒ
ⓐ 65 ⓑ 10 ⓒ 5
When we first introduced functions, we said a function is a relation that assigns to each element in its domain exactly one element in the range. For each ordered pair in the relation, each x-value is matched with only one y-value.
We used the birthday example to help us understand the definition. Every person has a birthday, but no one has two birthdays and it is okay for two people to share a birthday. Since each person has exactly one birthday, that relation is a function.
 A function is one-to-one if each value in the range has exactly one element in the domain. For each ordered pair in the function, each y-value is matched with only one x-value.
A function is one-to-one if each value in the range has exactly one element in the domain. For each ordered pair in the function, each y-value is matched with only one x-value.
Our example of the birthday relation is not a one-to-one function. Two people can share the same birthday. The range value August 2 is the birthday of Liz and June, and so one range value has two domain values. Therefore, the function is not one-to-one.
A function is one-to-one if each value in the range corresponds to one element in the domain. For each ordered pair in the function, each y-value is matched with only one x-value. There are no repeated y-values.
For each set of ordered pairs, determine if it represents a function and, if so, if the function is one-to-one.
ⓐ
and ⓑ
ⓐ* * *
Each x-value is matched with only one y-value. So this relation is a function.
But each y-value is not paired with only one x-value,
and
for example. So this function is not one-to-one.
ⓑ* * *
Each x-value is matched with only one y-value. So this relation is a function.
Since each y-value is paired with only one x-value, this function is one-to-one.
For each set of ordered pairs, determine if it represents a function and if so, is the function one-to-one.
ⓐ
ⓑ
ⓐ One-to-one function* * *
ⓑ Function; not one-to-one
For each set of ordered pairs, determine if it represents a function and if so, is the function one-to-one.
ⓐ
ⓑ
ⓐ Not a function* * *
ⓑ Function; not one-to-one
To help us determine whether a relation is a function, we use the vertical line test. A set of points in a rectangular coordinate system is the graph of a function if every vertical line intersects the graph in at most one point. Also, if any vertical line intersects the graph in more than one point, the graph does not represent a function.
The vertical line is representing an x-value and we check that it intersects the graph in only one y-value. Then it is a function.
To check if a function is one-to-one, we use a similar process. We use a horizontal line and check that each horizontal line intersects the graph in only one point. The horizontal line is representing a y-value and we check that it intersects the graph in only one x-value. If every horizontal line intersects the graph of a function in at most one point, it is a one-to-one function. This is the horizontal line test.
If every horizontal line intersects the graph of a function in at most one point, it is a one-to-one function.
We can test whether a graph of a relation is a function by using the vertical line test. We can then tell if the function is one-to-one by applying the horizontal line test.
Determine ⓐ whether each graph is the graph of a function and, if so, ⓑ whether it is one-to-one.
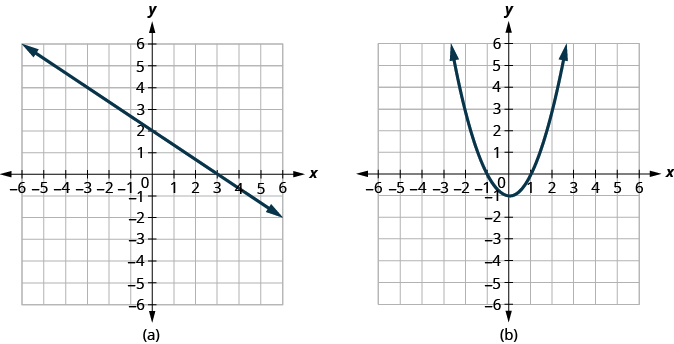
ⓐ* * *
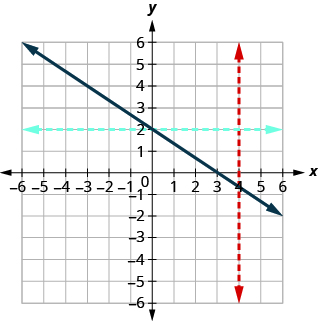 Since any vertical line intersects the graph in at most one point, the graph is the graph of a function. Since any horizontal line intersects the graph in at most one point, the graph is the graph of a one-to-one function.
Since any vertical line intersects the graph in at most one point, the graph is the graph of a function. Since any horizontal line intersects the graph in at most one point, the graph is the graph of a one-to-one function.
ⓑ* * *
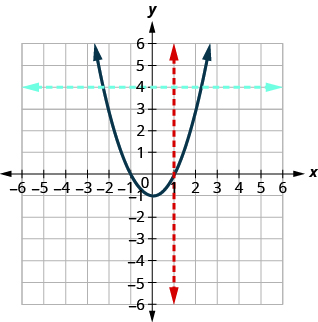 Since any vertical line intersects the graph in at most one point, the graph is the graph of a function. The horizontal line shown on the graph intersects it in two points. This graph does not represent a one-to-one function.
Since any vertical line intersects the graph in at most one point, the graph is the graph of a function. The horizontal line shown on the graph intersects it in two points. This graph does not represent a one-to-one function.
Determine ⓐ whether each graph is the graph of a function and, if so, ⓑ whether it is one-to-one.
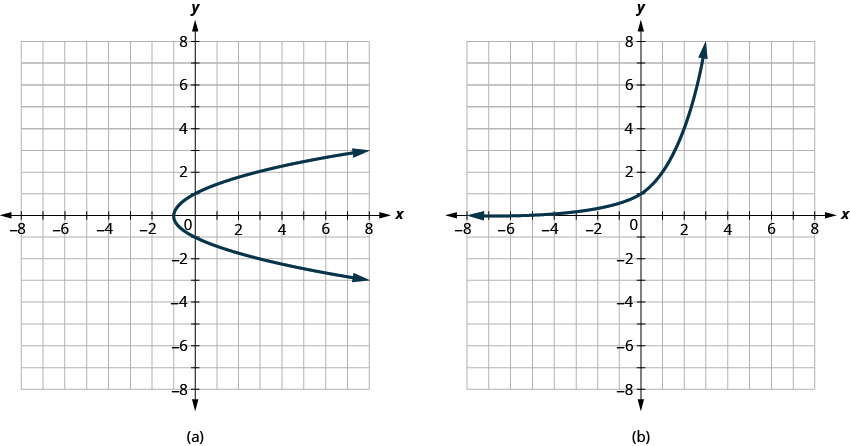
ⓐ Not a function ⓑ One-to-one function
Determine ⓐ whether each graph is the graph of a function and, if so, ⓑ whether it is one-to-one.
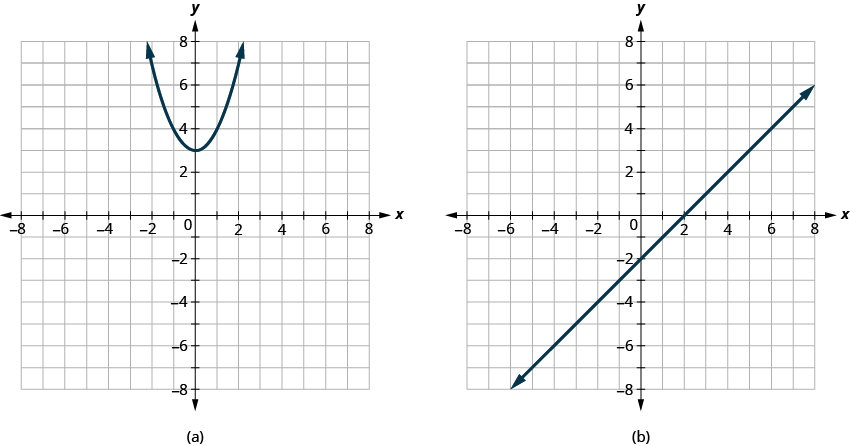
ⓐ Function; not one-to-one ⓑ One-to-one function
Let’s look at a one-to one function,
, represented by the ordered pairs
For each
-value,
adds 5 to get the
-value. To ‘undo’ the addition of 5, we subtract 5 from each
-value and get back to the original
-value. We can call this “taking the inverse of
” and name the function
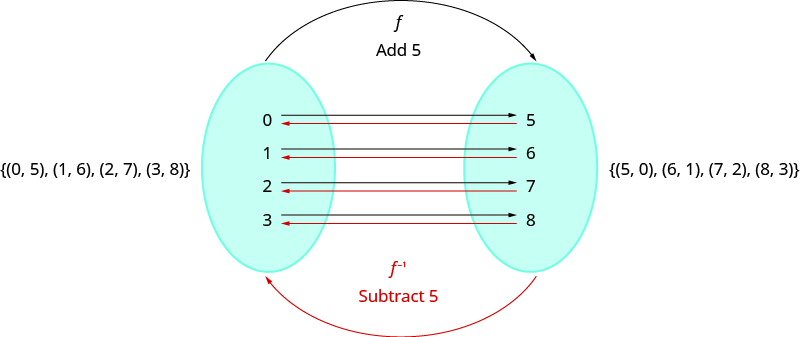 Notice that that the ordered pairs of
Notice that that the ordered pairs of
and
have their
-values and
-values reversed. The domain of
is the range of
and the domain of
is the range of
If
is a one-to-one function whose ordered pairs are of the form
then its inverse function
is the set of ordered pairs
In the next example we will find the inverse of a function defined by ordered pairs.
Find the inverse of the function
Determine the domain and range of the inverse function.
This function is one-to-one since every
-value is paired with exactly one
-value.
To find the inverse we reverse the
-values and
-values in the ordered pairs of the function.* * *
Find the inverse of
Determine the domain and range of the inverse function.
Inverse function:
Domain:
Range:
Find the inverse of
Determine the domain and range of the inverse function.
Inverse function:
Domain:
Range:
We just noted that if
is a one-to-one function whose ordered pairs are of the form
then its inverse function
is the set of ordered pairs
So if a point
is on the graph of a function
then the ordered pair
is on the graph of
See [link].
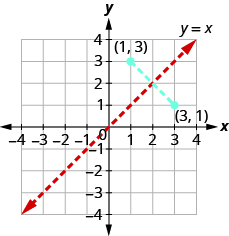
The distance between any two pairs
and
is cut in half by the line
So we say the points are mirror images of each other through the line
Since every point on the graph of a function
is a mirror image of a point on the graph of
we say the graphs are mirror images of each other through the line
We will use this concept to graph the inverse of a function in the next example.
Graph, on the same coordinate system, the inverse of the one-to one function shown.
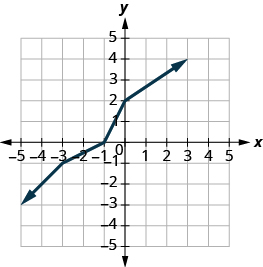
We can use points on the graph to find points on the inverse graph. Some points on the graph are:
.
So, the inverse function will contain the points:
.* * *
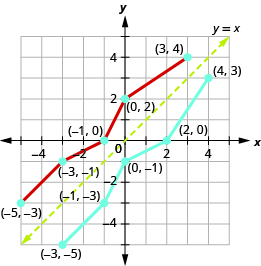 Notice how the graph of the original function and the graph of the inverse functions are mirror images through the line
Notice how the graph of the original function and the graph of the inverse functions are mirror images through the line
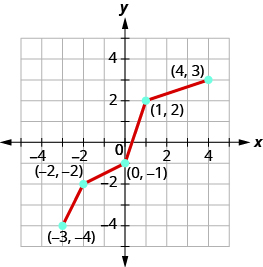
Graph, on the same coordinate system, the inverse of the one-to one function.
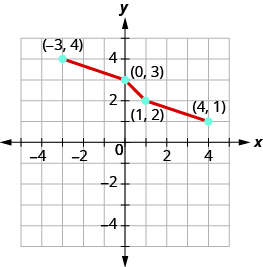
Graph, on the same coordinate system, the inverse of the one-to one function.
When we began our discussion of an inverse function, we talked about how the inverse function ‘undoes’ what the original function did to a value in its domain in order to get back to the original x-value.
 <div data-type="note">
<div data-type="note">
</div>
We can use this property to verify that two functions are inverses of each other.
Verify that
and
are inverse functions.
The functions are inverses of each other if
and
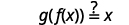 |
|
| {: valign=”top”} | Substitute |
for
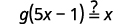 |
||
| {: valign=”top”} |  |
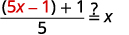 |
| {: valign=”top”} | Simplify. | 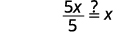 |
| {: valign=”top”} | Simplify. |  |
| {: valign=”top”} | ||
| {: valign=”top”} | 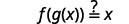 |
|
| {: valign=”top”} | Substitute |
for
| 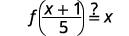 |
{: valign=”top”}|
|
{: valign=”top”}|  |
| 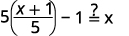 |
{: valign=”top”}| Simplify. |
|
{: valign=”top”}| Simplify. | 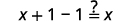 |
{: valign=”top”}| Simplify. |
|
{: valign=”top”}| Simplify. |  |
{: valign=”top”}{: .unnumbered .unstyled summary=”We want to examine whether g of f of x equals x In the first step, we substitute 5 x minus 1 for f of x which means that we are checking whether g of 5 x minus 1 equals x Then we find g of 5 x minus 1 where g of x equals the quantity x plus 1 all over 5. This means that we are trying to check whether the quantity 5 x plus 1 minus 1 all over 5 equals x. When we simplify we see that we are trying to check whether 5 x over 5 equals x. After simplifying further, we see that x equals x so this result holds. To investigate the other way, we are trying to determine whether f of g of x equals x. In the first step, we substitute the quantity x plus 1 all over 5 for g of x which means that we are trying to check whether f of quantity x plus 1 all over 5 equals x. Then we find f of quantity x plus 1 all over 5 where f of x equals 5 x minus 1. This means that we are trying to determine whether 5 times the quantity x plus 1 all over 5, minus 1 equals x. We simplify to see that to get x plus 1 minus 1 equals x. Simplifying further, we see that x does indeed equal x.” data-label=””}
|
{: valign=”top”}{: .unnumbered .unstyled summary=”We want to examine whether g of f of x equals x In the first step, we substitute 5 x minus 1 for f of x which means that we are checking whether g of 5 x minus 1 equals x Then we find g of 5 x minus 1 where g of x equals the quantity x plus 1 all over 5. This means that we are trying to check whether the quantity 5 x plus 1 minus 1 all over 5 equals x. When we simplify we see that we are trying to check whether 5 x over 5 equals x. After simplifying further, we see that x equals x so this result holds. To investigate the other way, we are trying to determine whether f of g of x equals x. In the first step, we substitute the quantity x plus 1 all over 5 for g of x which means that we are trying to check whether f of quantity x plus 1 all over 5 equals x. Then we find f of quantity x plus 1 all over 5 where f of x equals 5 x minus 1. This means that we are trying to determine whether 5 times the quantity x plus 1 all over 5, minus 1 equals x. We simplify to see that to get x plus 1 minus 1 equals x. Simplifying further, we see that x does indeed equal x.” data-label=””}
Since both
and
are true, the functions
and
are inverse functions. That is, they are inverses of each other.
Verify that the functions are inverse functions.
and
and
so they are inverses.
Verify that the functions are inverse functions.
and
and
so they are inverses.
We have found inverses of function defined by ordered pairs and from a graph. We will now look at how to find an inverse using an algebraic equation. The method uses the idea that if
is a one-to-one function with ordered pairs
then its inverse function
is the set of ordered pairs
If we reverse the x and y in the function and then solve for y, we get our inverse function.
Find the inverse of
Find the inverse of the function
Find the inverse of the function
We summarize the steps below.
for y.
Find the inverse of
Verify that the functions are inverses.* * *
Find the inverse of the function
Find the inverse of the function
and
is written
and is defined by
We read
as
of
of
is a one-to-one function whose ordered pairs are of the form
then its inverse function
is the set of ordered pairs
in the domain of one-to-one function
and
for
Find and Evaluate Composite Functions
In the following exercises, find ⓐ (f ∘ g)(x), ⓑ (g ∘ f)(x), and ⓒ (f · g)(x).
and
ⓐ
ⓑ
ⓒ* * *
and
and
ⓐ
ⓑ
ⓒ
and
and
ⓐ
ⓑ
ⓒ
and
and
ⓐ
ⓑ
ⓒ
and
In the following exercises, find the values described.
For functions
and
find* * *
ⓐ
ⓑ
ⓒ
ⓐ 245 ⓑ 104 ⓒ 53
For functions
and
find* * *
ⓐ
ⓑ
ⓒ
For functions
and
find* * *
ⓐ
ⓑ
ⓒ
ⓐ 250 ⓑ 14 ⓒ 77
For functions
and
find* * *
ⓐ
ⓑ
ⓒ
Determine Whether a Function is One-to-One
In the following exercises, determine if the set of ordered pairs represents a function and if so, is the function one-to-one.
,* * *
Function; not one-to-one
,* * *
,* * *
One-to-one function
,* * *
In the following exercises, determine whether each graph is the graph of a function and if so, is it one-to-one.
ⓐ* * *
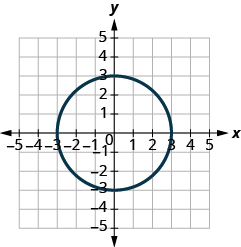
ⓑ* * *
ⓐ Not a function ⓑ Function; not one-to-one
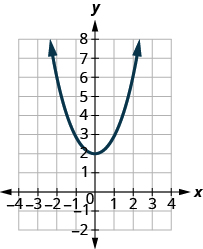
ⓐ* * *
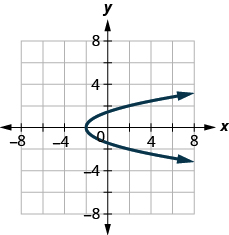
ⓑ* * *
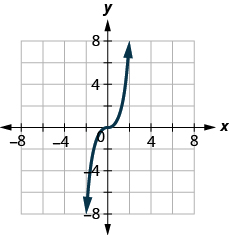
ⓐ* * *
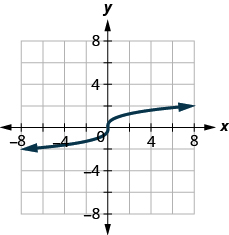
ⓑ* * *
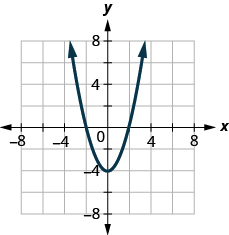
ⓐ One-to-one function* * *
ⓑ Function; not one-to-one
ⓐ* * *
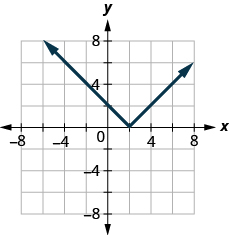
ⓑ* * *
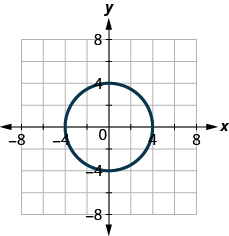
In the following exercises, find the inverse of each function. Determine the domain and range of the inverse function.
Inverse function:
Domain:
Range:
Inverse function:
Domain:
Range:
Inverse function:
Domain:
Range:
In the following exercises, graph, on the same coordinate system, the inverse of the one-to-one function shown.
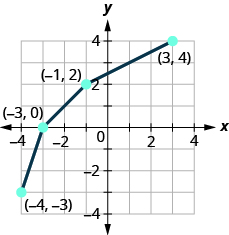
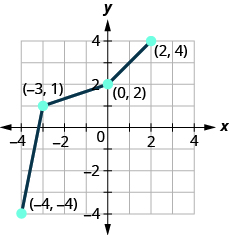
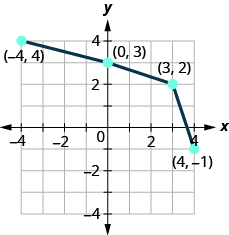
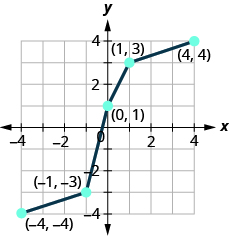
In the following exercises, determine whether or not the given functions are inverses.
and
and
so they are inverses.
and
and
and
so they are inverses.
and
and
and
so they are inverses.
and
and
and
so they are inverses (for nonnegative
and
In the following exercises, find the inverse of each function.
,
,
Explain how the graph of the inverse of a function is related to the graph of the function.
Answers will vary.
Explain how to find the inverse of a function from its equation. Use an example to demonstrate the steps.
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
 ⓑ If most of your checks were:
ⓑ If most of your checks were:
…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.
…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no—I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.

You can also download for free at http://cnx.org/contents/02776133-d49d-49cb-bfaa-67c7f61b25a1@4.13
Attribution: