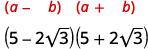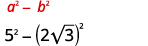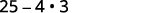Add, Subtract, and Multiply Radical Expressions
By the end of this section, you will be able to:
- Add and subtract radical expressions
- Multiply radical expressions
- Use polynomial multiplication to multiply radical expressions
Before you get started, take this readiness quiz.
- Add:
If you missed this problem, review [link].
- Simplify:
If you missed this problem, review [link].
- Simplify:
If you missed this problem, review [link].
Add and Subtract Radical Expressions
Adding radical expressions with the same index and the same radicand is just like adding like terms. We call radicals with the same index and the same radicand like radicals to remind us they work the same as like terms.
Like Radicals
Like radicals are radical expressions with the same index and the same radicand.
We add and subtract like radicals in the same way we add and subtract like terms. We know that
is
Similarly we add
and the result is
Think about adding like terms with variables as you do the next few examples. When you have like radicals, you just add or subtract the coefficients. When the radicals are not like, you cannot combine the terms.
Simplify: ⓐ
ⓑ
ⓒ
ⓐ* * *
ⓑ* * *
ⓒ* * *
The indices are the same but the radicals are different. These are not like radicals. Since the radicals are not like, we cannot subtract them.
Simplify: ⓐ
ⓑ
ⓒ
Simplify: ⓐ
ⓑ
ⓒ
For radicals to be like, they must have the same index and radicand. When the radicands contain more than one variable, as long as all the variables and their exponents are identical, the radicands are the same.
Simplify: ⓐ
ⓑ
ⓐ* * *
ⓑ* * *
Simplify: ⓐ
ⓑ
Simplify: ⓐ
ⓑ
Remember that we always simplify radicals by removing the largest factor from the radicand that is a power of the index. Once each radical is simplified, we can then decide if they are like radicals.
Simplify: ⓐ
ⓑ
ⓒ
ⓐ* * *
ⓑ* * *
ⓒ* * *
Simplify: ⓐ
ⓑ
ⓒ
Simplify: ⓐ
ⓑ
ⓒ
In the next example, we will remove both constant and variable factors from the radicals. Now that we have practiced taking both the even and odd roots of variables, it is common practice at this point for us to assume all variables are greater than or equal to zero so that absolute values are not needed. We will use this assumption thoughout the rest of this chapter.
Simplify: ⓐ
ⓑ
ⓐ* * *
ⓑ* * *
Simplify: ⓐ
ⓑ
Simplify: ⓐ
ⓑ
Multiply Radical Expressions
We have used the Product Property of Roots to simplify square roots by removing the perfect square factors. We can use the Product Property of Roots ‘in reverse’ to multiply square roots. Remember, we assume all variables are greater than or equal to zero.
We will rewrite the Product Property of Roots so we see both ways together.
Product Property of Roots
For any real numbers,
and
and for any integer
When we multiply two radicals they must have the same index. Once we multiply the radicals, we then look for factors that are a power of the index and simplify the radical whenever possible.
Multiplying radicals with coefficients is much like multiplying variables with coefficients. To multiply
we multiply the coefficients together and then the variables. The result is 12xy. Keep this in mind as you do these examples.
Simplify: ⓐ
ⓑ
ⓐ* * *
ⓑ* * *
Simplify: ⓐ
ⓑ
Simplify: ⓐ
ⓑ
We follow the same procedures when there are variables in the radicands.
Simplify: ⓐ
ⓑ
ⓐ* * *
ⓑ When the radicands involve large numbers, it is often advantageous to factor them in order to find the perfect powers.
Simplify: ⓐ
ⓑ
Simplify: ⓐ
ⓑ
Use Polynomial Multiplication to Multiply Radical Expressions
In the next a few examples, we will use the Distributive Property to multiply expressions with radicals. First we will distribute and then simplify the radicals when possible.
Simplify: ⓐ
ⓑ
ⓐ* * *
ⓑ* * *
Simplify: ⓐ
ⓑ
Simplify: ⓐ
ⓑ
When we worked with polynomials, we multiplied binomials by binomials. Remember, this gave us four products before we combined any like terms. To be sure to get all four products, we organized our work—usually by the FOIL method.
Simplify: ⓐ
ⓑ
ⓐ* * *
ⓑ* * *
Simplify: ⓐ
ⓑ
Simplify: ⓐ
ⓑ
Recognizing some special products made our work easier when we multiplied binomials earlier. This is true when we multiply radicals, too. The special product formulas we used are shown here.
Special Products
We will use the special product formulas in the next few examples. We will start with the Product of Binomial Squares Pattern.
Simplify: ⓐ
ⓑ
Simplify: ⓐ
ⓑ
Simplify: ⓐ
ⓑ
In the next example, we will use the Product of Conjugates Pattern. Notice that the final product has no radical.
Key Concepts
- Product Property of Roots
- For any real numbers,
and
and for any integer
and
- Special Products
Practice Makes Perfect
Add and Subtract Radical Expressions
In the following exercises, simplify.
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ
ⓑ
Multiply Radical Expressions
In the following exercises, simplify.
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ
ⓑ
Use Polynomial Multiplication to Multiply Radical Expressions
In the following exercises, multiply.
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ
ⓑ
Mixed Practice
Writing Exercises
Explain the when a radical expression is in simplest form.
Explain the process for determining whether two radicals are like or unlike. Make sure your answer makes sense for radicals containing both numbers and variables.
ⓐ Explain why
is always non-negative, for
ⓑ Explain why
is always non-positive, for
Use the binomial square pattern to simplify
Explain all your steps.
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
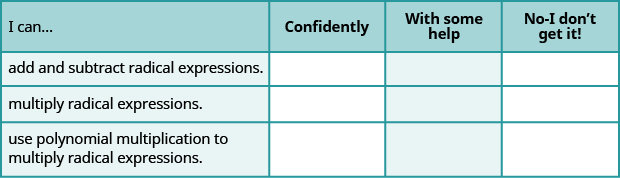 ⓑ On a scale of 1-10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?
ⓑ On a scale of 1-10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?
Glossary
- like radicals
- Like radicals are radical expressions with the same index and the same radicand.

This work is licensed under a Creative Commons Attribution 4.0 International License.
You can also download for free at http://cnx.org/contents/02776133-d49d-49cb-bfaa-67c7f61b25a1@4.13
Attribution:
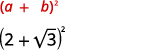 |
{: valign=”top”}| Multiply, using the Product of Binomial Squares Pattern. |
|
{: valign=”top”}| Multiply, using the Product of Binomial Squares Pattern. | 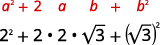 |
{: valign=”top”}| Simplify. |
|
{: valign=”top”}| Simplify. | 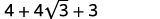 |
{: valign=”top”}| Combine like terms. |
|
{: valign=”top”}| Combine like terms. |  |
{: valign=”top”}{: .unnumbered .unstyled summary=”The binomial square formula tells us that the quantity a plus b in parentheses squared is equal to a squared plus 2 a b plus b squared. Then the quantity 2 plus square root 3 in parentheses squared is equal to 2 squared plus 2 times 2 times square root 3 plus the quantity square root 3 in parentheses squared. Simplifying we get 4 plus 4 square root 3 plus 3. Combining like terms we get 7 plus 4 square root 3.” data-label=””}
|
{: valign=”top”}{: .unnumbered .unstyled summary=”The binomial square formula tells us that the quantity a plus b in parentheses squared is equal to a squared plus 2 a b plus b squared. Then the quantity 2 plus square root 3 in parentheses squared is equal to 2 squared plus 2 times 2 times square root 3 plus the quantity square root 3 in parentheses squared. Simplifying we get 4 plus 4 square root 3 plus 3. Combining like terms we get 7 plus 4 square root 3.” data-label=””}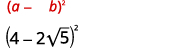 |
{: valign=”top”}| Multiply, using the Product of Binomial Squares Pattern. |
|
{: valign=”top”}| Multiply, using the Product of Binomial Squares Pattern. | 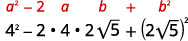 |
{: valign=”top”}| Simplify. |
|
{: valign=”top”}| Simplify. | 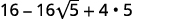 |
{: valign=”top”}| |
|
{: valign=”top”}| | 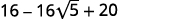 |
{: valign=”top”}| Combine like terms. |
|
{: valign=”top”}| Combine like terms. |  |
{: valign=”top”}{: .unnumbered .unstyled .can-break summary=”The binomial square formula tells us that the quantity a minus b in parentheses squared is equal to a squared minus 2 a b plus b squared. Then the quantity 4 minus 2 square root 5 in parentheses squared is equal to 4 squared minus 2 times 4 times 2 square root 5 plus the quantity 2 square root 5 in parentheses squared. Simplifying we get 16 minus 16 square root 5 plus 4 times 5. Simplifying we get 16 minus 16 square root 5 plus 20. Combining like terms we get 36 minus 16 square root 5.” data-label=””}
|
{: valign=”top”}{: .unnumbered .unstyled .can-break summary=”The binomial square formula tells us that the quantity a minus b in parentheses squared is equal to a squared minus 2 a b plus b squared. Then the quantity 4 minus 2 square root 5 in parentheses squared is equal to 4 squared minus 2 times 4 times 2 square root 5 plus the quantity 2 square root 5 in parentheses squared. Simplifying we get 16 minus 16 square root 5 plus 4 times 5. Simplifying we get 16 minus 16 square root 5 plus 20. Combining like terms we get 36 minus 16 square root 5.” data-label=””}