Simplify Radical Expressions
By the end of this section, you will be able to:
- Use the Product Property to simplify radical expressions
- Use the Quotient Property to simplify radical expressions
Before you get started, take this readiness quiz.
- Simplify:
If you missed this problem, review [link].
- Simplify:
If you missed this problem, review [link].
- Simplify:
If you missed this problem, review [link].
Use the Product Property to Simplify Radical Expressions
We will simplify radical expressions in a way similar to how we simplified fractions. A fraction is simplified if there are no common factors in the numerator and denominator. To simplify a fraction, we look for any common factors in the numerator and denominator.
A radical expression,
is considered simplified if it has no factors of
So, to simplify a radical expression, we look for any factors in the radicand that are powers of the index.
Simplified Radical Expression
For real numbers a and m, and
For example,
is considered simplified because there are no perfect square factors in 5. But
is not simplified because 12 has a perfect square factor of 4.
Similarly,
is simplified because there are no perfect cube factors in 4. But
is not simplified because 24 has a perfect cube factor of 8.
To simplify radical expressions, we will also use some properties of roots. The properties we will use to simplify radical expressions are similar to the properties of exponents. We know that
The corresponding of Product Property of Roots says that
Product Property of *n*th Roots
If
and
are real numbers, and
is an integer, then
We use the Product Property of Roots to remove all perfect square factors from a square root.
Simplify Square Roots Using the Product Property of Roots
  
Notice in the previous example that the simplified form of
is
which is the product of an integer and a square root. We always write the integer in front of the square root.
Be careful to write your integer so that it is not confused with the index. The expression
is very different from
Simplify a radical expression using the Product Property.
- Find the largest factor in the radicand that is a perfect power of the index. Rewrite the radicand as a product of two factors, using that factor.
- Use the product rule to rewrite the radical as the product of two radicals.
- Simplify the root of the perfect power.
We will apply this method in the next example. It may be helpful to have a table of perfect squares, cubes, and fourth powers.
Simplify: ⓐ
ⓑ
ⓒ
ⓐ* * *
ⓑ* * *
ⓒ* * *
Simplify: ⓐ
ⓑ
ⓒ
Simplify: ⓐ
ⓑ
ⓒ
The next example is much like the previous examples, but with variables. Don’t forget to use the absolute value signs when taking an even root of an expression with a variable in the radical.
Simplify: ⓐ
ⓑ
ⓒ
ⓐ* * *
ⓑ* * *
ⓒ* * *
Simplify: ⓐ
ⓑ
ⓒ
Simplify: ⓐ
ⓑ
ⓒ
We follow the same procedure when there is a coefficient in the radicand. In the next example, both the constant and the variable have perfect square factors.
Simplify: ⓐ
ⓑ
ⓒ
ⓐ* * *
ⓑ* * *
ⓒ* * *
Simplify: ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
Simplify: ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
In the next example, we continue to use the same methods even though there are more than one variable under the radical.
Simplify: ⓐ
ⓑ
ⓒ
ⓐ* * *
ⓑ* * *
ⓒ* * *
Simplify: ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
Simplify: ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ* * *
ⓑ* * *
Simplify: ⓐ
ⓑ
We have seen how to use the order of operations to simplify some expressions with radicals. In the next example, we have the sum of an integer and a square root. We simplify the square root but cannot add the resulting expression to the integer since one term contains a radical and the other does not. The next example also includes a fraction with a radical in the numerator. Remember that in order to simplify a fraction you need a common factor in the numerator and denominator.
Simplify: ⓐ
ⓑ
ⓐ* * *
The terms cannot be added as one has a radical and the other does not. Trying to add an integer and a radical is like trying to add an integer and a variable. They are not like terms!
ⓑ* * *
Simplify: ⓐ
ⓑ
Use the Quotient Property to Simplify Radical Expressions
Whenever you have to simplify a radical expression, the first step you should take is to determine whether the radicand is a perfect power of the index. If not, check the numerator and denominator for any common factors, and remove them. You may find a fraction in which both the numerator and the denominator are perfect powers of the index.
Simplify: ⓐ
ⓑ
ⓒ
ⓐ* * *
ⓑ* * *
ⓒ* * *
Simplify: ⓐ
ⓑ
ⓒ
Simplify: ⓐ
ⓑ
ⓒ
In the last example, our first step was to simplify the fraction under the radical by removing common factors. In the next example we will use the Quotient Property to simplify under the radical. We divide the like bases by subtracting their exponents,
Simplify: ⓐ
ⓑ
ⓒ
ⓐ* * *
ⓑ* * *
ⓒ* * *
Simplify: ⓐ
ⓑ
ⓒ
Simplify: ⓐ
ⓑ
ⓒ
Remember the Quotient to a Power Property? It said we could raise a fraction to a power by raising the numerator and denominator to the power separately.
We can use a similar property to simplify a root of a fraction. After removing all common factors from the numerator and denominator, if the fraction is not a perfect power of the index, we simplify the numerator and denominator separately.
Quotient Property of Radical Expressions
If
and
are real numbers,
and for any integer
then,
How to Simplify the Quotient of Radical Expressions
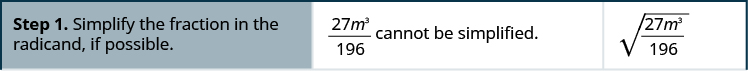  
Simplify a square root using the Quotient Property.
- Simplify the fraction in the radicand, if possible.
- Use the Quotient Property to rewrite the radical as the quotient of two radicals.
- Simplify the radicals in the numerator and the denominator.
Simplify: ⓐ
ⓑ
ⓒ
ⓐ* * *
ⓑ* * *
ⓒ* * *
Simplify: ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
Simplify: ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
Be sure to simplify the fraction in the radicand first, if possible.
Simplify: ⓐ
ⓑ
ⓒ
ⓐ* * *
ⓑ* * *
ⓒ* * *
Simplify: ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
Simplify: ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
In the next example, there is nothing to simplify in the denominators. Since the index on the radicals is the same, we can use the Quotient Property again, to combine them into one radical. We will then look to see if we can simplify the expression.
Simplify: ⓐ
ⓑ
ⓒ
ⓐ* * *
ⓑ* * *
ⓒ* * *
Simplify: ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
Simplify: ⓐ
ⓑ
ⓒ
Key Concepts
Practice Makes Perfect
Use the Product Property to Simplify Radical Expressions
In the following exercises, use the Product Property to simplify radical expressions.
In the following exercises, simplify using absolute value signs as needed.
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
Use the Quotient Property to Simplify Radical Expressions
In the following exercises, use the Quotient Property to simplify square roots.
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
Writing Exercises
Explain why
Then explain why
Explain why
is not equal to
Explain how you know that
Explain why
is not a real number but
is.
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
 ⓑ After reviewing this checklist, what will you do to become confident for all objectives?
ⓑ After reviewing this checklist, what will you do to become confident for all objectives?

This work is licensed under a Creative Commons Attribution 4.0 International License.
You can also download for free at http://cnx.org/contents/02776133-d49d-49cb-bfaa-67c7f61b25a1@4.13
Attribution:
 ⓑ After reviewing this checklist, what will you do to become confident for all objectives?
ⓑ After reviewing this checklist, what will you do to become confident for all objectives?