 Removing the x’s from
Removing the x’s from By the end of this section, you will be able to:
Before you get started, take this readiness quiz.
We previously reviewed the properties of fractions and their operations. We introduced rational numbers, which are just fractions where the numerators and denominators are integers. In this chapter, we will work with fractions whose numerators and denominators are polynomials. We call this kind of expression a rational expression.
A rational expression is an expression of the form
where p and q are polynomials and
Here are some examples of rational expressions:
Notice that the first rational expression listed above,
, is just a fraction. Since a constant is a polynomial with degree zero, the ratio of two constants is a rational expression, provided the denominator is not zero.
We will do the same operations with rational expressions that we did with fractions. We will simplify, add, subtract, multiply, divide and use them in applications.
If the denominator is zero, the rational expression is undefined. The numerator of a rational expression may be 0—but not the denominator.
When we work with a numerical fraction, it is easy to avoid dividing by zero because we can see the number in the denominator. In order to avoid dividing by zero in a rational expression, we must not allow values of the variable that will make the denominator be zero.
So before we begin any operation with a rational expression, we examine it first to find the values that would make the denominator zero. That way, when we solve a rational equation for example, we will know whether the algebraic solutions we find are allowed or not.
Determine the value for which each rational expression is undefined:
ⓐ
ⓑ
ⓒ
The expression will be undefined when the denominator is zero.
ⓐ* * *
ⓑ* * *
ⓒ* * *
Determine the value for which each rational expression is undefined.
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
Determine the value for which each rational expression is undefined.
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
A fraction is considered simplified if there are no common factors, other than 1, in its numerator and denominator. Similarly, a simplified rational expression has no common factors, other than 1, in its numerator and denominator.
A rational expression is considered simplified if there are no common factors in its numerator and denominator.
For example,
We use the Equivalent Fractions Property to simplify numerical fractions. We restate it here as we will also use it to simplify rational expressions.
If a, b, and c are numbers where
Notice that in the Equivalent Fractions Property, the values that would make the denominators zero are specifically disallowed. We see
clearly stated.
To simplify rational expressions, we first write the numerator and denominator in factored form. Then we remove the common factors using the Equivalent Fractions Property.
Be very careful as you remove common factors. Factors are multiplied to make a product. You can remove a factor from a product. You cannot remove a term from a sum.
 Removing the x’s from
Removing the x’s from
would be like cancelling the 2’s in the fraction
Simplify:
.
Simplify:
Simplify:
We now summarize the steps you should follow to simplify rational expressions.
Usually, we leave the simplified rational expression in factored form. This way, it is easy to check that we have removed all the common factors.
We’ll use the methods we have learned to factor the polynomials in the numerators and denominators in the following examples.
Every time we write a rational expression, we should make a statement disallowing values that would make a denominator zero. However, to let us focus on the work at hand, we will omit writing it in the examples.
Simplify:
.
Simplify:
.
Simplify:
.
Now we will see how to simplify a rational expression whose numerator and denominator have opposite factors. We previously introduced opposite notation: the opposite of a is
and
The numerical fraction, say
simplifies to
. We also recognize that the numerator and denominator are opposites.
The fraction
, whose numerator and denominator are opposites also simplifies to
.
This tells us that
is the opposite of
In general, we could write the opposite of
as
So the rational expression
simplifies to
The opposite of
is
An expression and its opposite divide to
We will use this property to simplify rational expressions that contain opposites in their numerators and denominators. Be careful not to treat
and
as opposites. Recall that in addition, order doesn’t matter so
. So if
, then
Simplify:
| | 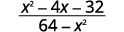 |
{: valign=”top”}| Factor the numerator and the denominator. |
|
{: valign=”top”}| Factor the numerator and the denominator. | 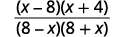 |
{: valign=”top”}| Recognize the factors that are opposites. |
|
{: valign=”top”}| Recognize the factors that are opposites. | 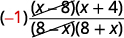 |
{: valign=”top”}| Simplify. |
|
{: valign=”top”}| Simplify. | 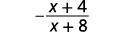 |
{: valign=”top”}{: .unnumbered .unstyled summary=”Factor the numerator and denominator of the rational expression, the quantity x squared minus 4 x minus 32 divided by the quantity 64 minus x squared. The numerator factors into the quantity x minus 8 times the quantity x plus 4. The denominator factors into the quantity 8 minus x times the quantity 8 plus x. The factors x minus 8 and 8 minus x are opposites, so multiply the rational expression by negative 1. The result is the negative of the quantity x plus 4 divided by the quantity x plus 8.” data-label=””}
|
{: valign=”top”}{: .unnumbered .unstyled summary=”Factor the numerator and denominator of the rational expression, the quantity x squared minus 4 x minus 32 divided by the quantity 64 minus x squared. The numerator factors into the quantity x minus 8 times the quantity x plus 4. The denominator factors into the quantity 8 minus x times the quantity 8 plus x. The factors x minus 8 and 8 minus x are opposites, so multiply the rational expression by negative 1. The result is the negative of the quantity x plus 4 divided by the quantity x plus 8.” data-label=””}
Simplify:
Simplify:
To multiply rational expressions, we do just what we did with numerical fractions. We multiply the numerators and multiply the denominators. Then, if there are any common factors, we remove them to simplify the result.
If p, q, r, and s are polynomials where
then
To multiply rational expressions, multiply the numerators and multiply the denominators.
Remember, throughout this chapter, we will assume that all numerical values that would make the denominator be zero are excluded. We will not write the restrictions for each rational expression, but keep in mind that the denominator can never be zero. So in this next example,
and
Simplify:
Simplify:
Simplify:
Multiply:
Simplify:
Simplify:
Just like we did for numerical fractions, to divide rational expressions, we multiply the first fraction by the reciprocal of the second.
If p, q, r, and s are polynomials where
then
To divide rational expressions, multiply the first fraction by the reciprocal of the second.
Once we rewrite the division as multiplication of the first expression by the reciprocal of the second, we then factor everything and look for common factors.
Divide:
Simplify:
Simplify:
Recall from Use the Language of Algebra that a complex fraction is a fraction that contains a fraction in the numerator, the denominator or both. Also, remember a fraction bar means division. A complex fraction is another way of writing division of two fractions.
Divide:
Simplify:
Simplify:
If we have more than two rational expressions to work with, we still follow the same procedure. The first step will be to rewrite any division as multiplication by the reciprocal. Then, we factor and multiply.
Perform the indicated operations:
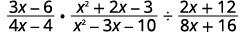 |
|
| Rewrite the division as multiplication by the reciprocal. |
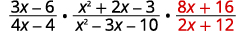 |
| Factor the numerators and the denominators. | 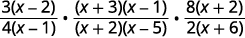 |
| Multiply the fractions. Bringing the constants to the front will help when removing common factors. |
|
| Simplify by dividing out common factors. | 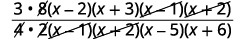 |
| Simplify. | 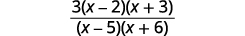 |
Perform the indicated operations:
Perform the indicated operations:
We started this section stating that a rational expression is an expression of the form
where p and q are polynomials and
Similarly, we define a rational function as a function of the form
where
and
are polynomial functions and
is not zero.
A rational function is a function of the form
where
and
are polynomial functions and
is not zero.
The domain of a rational function is all real numbers except for those values that would cause division by zero. We must eliminate any values that make
Find the domain of
The domain will be all real numbers except those values that make the denominator zero. We will set the denominator equal to zero , solve that equation, and then exclude those values from the domain.
Find the domain of
The domain of
is all real numbers where
and
Find the domain of
The domain of
is all real numbers where
and
To multiply rational functions, we multiply the resulting rational expressions on the right side of the equation using the same techniques we used to multiply rational expressions.
Find
where
and
Find
where
and
Find
where
and
To divide rational functions, we divide the resulting rational expressions on the right side of the equation using the same techniques we used to divide rational expressions.
Find
where
and
Find
where
and
Find
where
and
If a, b, and c are numbers where
then
and
The opposite of
is
An expression and its opposite divide to
If p, q, r, and s are polynomials where
then
If p, q, r, and s are polynomials where
then
Determine the Values for Which a Rational Expression is Undefined
In the following exercises, determine the values for which the rational expression is undefined.
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
ⓐ
ⓑ
ⓒ
Simplify Rational Expressions
In the following exercises, simplify each rational expression.
Multiply Rational Expressions
In the following exercises, multiply the rational expressions.
Divide Rational Expressions
In the following exercises, divide the rational expressions.
For the following exercises, perform the indicated operations.
Multiply and Divide Rational Functions
In the following exercises, find the domain of each function.
and
and
For the following exercises, find
where
and
are given.
For the following exercises, find
where
and
are given.
Explain how you find the values of x for which the rational expression
is undefined.
Answers will vary.
Explain all the steps you take to simplify the rational expression
ⓐ Multiply
and explain all your steps.* * *
ⓑ Multiply
and explain all your steps.* * *
ⓒ Evaluate your answer to part ⓑ when
. Did you get the same answer you got in part ⓐ? Why or why not?
Answers will vary.
ⓐ Divide
and explain all your steps.* * *
ⓑ Divide
and explain all your steps.* * *
ⓒ Evaluate your answer to part ⓑ when
Did you get the same answer you got in part ⓐ? Why or why not?
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
 ⓑ If most of your checks were:
ⓑ If most of your checks were:
…confidently. Congratulations! You have achieved your goals in this section! Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific!
…with some help. This must be addressed quickly as topics you do not master become potholes in your road to success. Math is sequential - every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no - I don’t get it! This is critical and you must not ignore it. You need to get help immediately or you will quickly be overwhelmed. See your instructor as soon as possible to discuss your situation. Together you can come up with a plan to get you the help you need.
where p and q are polynomials and
where
and
are polynomial functions and
is not zero.

You can also download for free at http://cnx.org/contents/02776133-d49d-49cb-bfaa-67c7f61b25a1@4.13
Attribution: