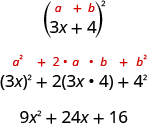 The trinomial
The trinomial By the end of this section, you will be able to:
Before you get started, take this readiness quiz.
We have seen that some binomials and trinomials result from special products—squaring binomials and multiplying conjugates. If you learn to recognize these kinds of polynomials, you can use the special products patterns to factor them much more quickly.
Some trinomials are perfect squares. They result from multiplying a binomial times itself. We squared a binomial using the Binomial Squares pattern in a previous chapter.
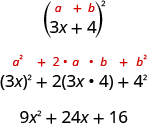 The trinomial
The trinomial
is called a perfect square trinomial. It is the square of the binomial
In this chapter, you will start with a perfect square trinomial and factor it into its prime factors.
You could factor this trinomial using the methods described in the last section, since it is of the form
But if you recognize that the first and last terms are squares and the trinomial fits the perfect square trinomials pattern, you will save yourself a lot of work.
Here is the pattern—the reverse of the binomial squares pattern.
If a and b are real numbers
To make use of this pattern, you have to recognize that a given trinomial fits it. Check first to see if the leading coefficient is a perfect square,
Next check that the last term is a perfect square,
Then check the middle term—is it the product,
If everything checks, you can easily write the factors.
Factor:
Factor:
Factor:
The sign of the middle term determines which pattern we will use. When the middle term is negative, we use the pattern
which factors to
The steps are summarized here.
We’ll work one now where the middle term is negative.
Factor:
The first and last terms are squares. See if the middle term fits the pattern of a perfect square trinomial. The middle term is negative, so the binomial square would be
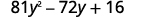 |
|
| Are the first and last terms perfect squares? |  |
| Check the middle term. | 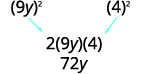 |
| Does it match Yes. | 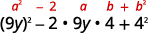 |
| Write as the square of a binomial. | 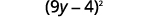 |
| Check by multiplying: |
Factor:
Factor:
The next example will be a perfect square trinomial with two variables.
Factor:
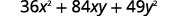 |
|
| Test each term to verify the pattern. | 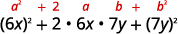 |
| Factor. | 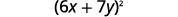 |
| Check by multiplying. |
Factor:
Factor:
Remember the first step in factoring is to look for a greatest common factor. Perfect square trinomials may have a GCF in all three terms and it should be factored out first. And, sometimes, once the GCF has been factored, you will recognize a perfect square trinomial.
Factor:
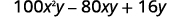 |
|
| {: valign=”top”} | Is there a GCF? Yes, |
so factor it out. | 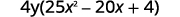 |
{: valign=”top”}| Is this a perfect square trinomial? | |
{: valign=”top”}| Verify the pattern. |
|
{: valign=”top”}| Is this a perfect square trinomial? | |
{: valign=”top”}| Verify the pattern. | 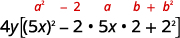 |
{: valign=”top”}| Factor. |
|
{: valign=”top”}| Factor. | 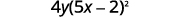 |
{: valign=”top”}{: .unnumbered .unstyled summary=”Is there a GCF in 100 x squared y minus 80xy plus 16y? Yes. Factoring it out, we get 4y open parentheses 25 x squared minus 20x plus 4 close parentheses. Is this a perfect square trinomial? To verify the pattern, we rewrite as 4y open bracket open parentheses 5x close parentheses squared minus 2 times 5x times 2 plus 2 squared close bracket. Factor to get 4y open parentheses 5x minus 2 close parentheses squared. Finally, we check by multiplying.” data-label=””}
|
{: valign=”top”}{: .unnumbered .unstyled summary=”Is there a GCF in 100 x squared y minus 80xy plus 16y? Yes. Factoring it out, we get 4y open parentheses 25 x squared minus 20x plus 4 close parentheses. Is this a perfect square trinomial? To verify the pattern, we rewrite as 4y open bracket open parentheses 5x close parentheses squared minus 2 times 5x times 2 plus 2 squared close bracket. Factor to get 4y open parentheses 5x minus 2 close parentheses squared. Finally, we check by multiplying.” data-label=””}
Remember: Keep the factor 4y in the final product.
Check:* * *
Factor:
Factor:
The other special product you saw in the previous chapter was the Product of Conjugates pattern. You used this to multiply two binomials that were conjugates. Here’s an example:
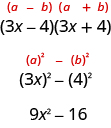 A difference of squares factors to a product of conjugates.
A difference of squares factors to a product of conjugates.
If a and b are real numbers,
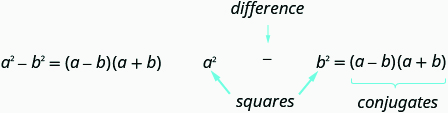
Remember, “difference” refers to subtraction. So, to use this pattern you must make sure you have a binomial in which two squares are being subtracted.
Factor:
Factor:
Factor:
It is important to remember that sums of squares do not factor into a product of binomials. There are no binomial factors that multiply together to get a sum of squares. After removing any GCF, the expression
is prime!
The next example shows variables in both terms.
Factor:
Factor:
Factor:
As always, you should look for a common factor first whenever you have an expression to factor. Sometimes a common factor may “disguise” the difference of squares and you won’t recognize the perfect squares until you factor the GCF.
Also, to completely factor the binomial in the next example, we’ll factor a difference of squares twice!
Factor:
The last factor, the sum of squares, cannot be factored.
Factor:
Factor:
The next example has a polynomial with 4 terms. So far, when this occurred we grouped the terms in twos and factored from there. Here we will notice that the first three terms form a perfect square trinomial.
Factor:
Notice that the first three terms form a perfect square trinomial.
| | 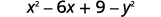 |
{: valign=”top”}| Factor by grouping the first three terms. |
|
{: valign=”top”}| Factor by grouping the first three terms. | 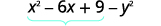 |
{: valign=”top”}| Use the perfect square trinomial pattern. |
|
{: valign=”top”}| Use the perfect square trinomial pattern. | 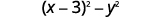 |
{: valign=”top”}| Is this a difference of squares? Yes. | |
{: valign=”top”}| Yes—write them as squares. |
|
{: valign=”top”}| Is this a difference of squares? Yes. | |
{: valign=”top”}| Yes—write them as squares. | 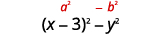 |
{: valign=”top”}| Factor as the product of conjugates. |
|
{: valign=”top”}| Factor as the product of conjugates. | 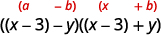 |
{: valign=”top”}| |
|
{: valign=”top”}| | 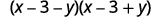 |
{: valign=”top”}{: .unnumbered .unstyled summary=”We have x squared minus 6x plus 9 minus y squared. We factor by grouping the first three terms. Use the perfect square trinomial pattern to get open parentheses x minus 3 close parentheses squared minus y squared. Is this a difference of squares? Yes. Factor as the product of conjugates, open parentheses x minus 3 minus y close parentheses open parentheses x minus 3 plus y close parentheses. You may want to rewrite the solution as open parentheses x minus y minus 3 close parentheses open parentheses x plus y minus 3 close parentheses.” data-label=””}
|
{: valign=”top”}{: .unnumbered .unstyled summary=”We have x squared minus 6x plus 9 minus y squared. We factor by grouping the first three terms. Use the perfect square trinomial pattern to get open parentheses x minus 3 close parentheses squared minus y squared. Is this a difference of squares? Yes. Factor as the product of conjugates, open parentheses x minus 3 minus y close parentheses open parentheses x minus 3 plus y close parentheses. You may want to rewrite the solution as open parentheses x minus y minus 3 close parentheses open parentheses x plus y minus 3 close parentheses.” data-label=””}
You may want to rewrite the solution as
Factor:
Factor:
There is another special pattern for factoring, one that we did not use when we multiplied polynomials. This is the pattern for the sum and difference of cubes. We will write these formulas first and then check them by multiplication.
We’ll check the first pattern and leave the second to you.
| | 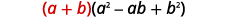 |
{: valign=”top”}| Distribute. |
|
{: valign=”top”}| Distribute. | 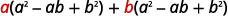 |
{: valign=”top”}| Multiply. |
|
{: valign=”top”}| Multiply. | 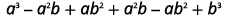 |
{: valign=”top”}| Combine like terms. |
|
{: valign=”top”}| Combine like terms. | 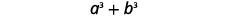 |
{: valign=”top”}{: .unnumbered .unstyled summary=”Open parentheses a plus b close parentheses open parentheses a squared minus ab plus b squared. Distribute: a open parentheses a squared minus ab plus b squared plus b open parentheses a squared minus ab plus b squared close parentheses. Multiply: a cubed minus a squared b plus ab squared plus a squared b minus ab squared plus b cubed. Combine like terms: a cubed plus b cubed.” data-label=””}
|
{: valign=”top”}{: .unnumbered .unstyled summary=”Open parentheses a plus b close parentheses open parentheses a squared minus ab plus b squared. Distribute: a open parentheses a squared minus ab plus b squared plus b open parentheses a squared minus ab plus b squared close parentheses. Multiply: a cubed minus a squared b plus ab squared plus a squared b minus ab squared plus b cubed. Combine like terms: a cubed plus b cubed.” data-label=””}
The two patterns look very similar, don’t they? But notice the signs in the factors. The sign of the binomial factor matches the sign in the original binomial. And the sign of the middle term of the trinomial factor is the opposite of the sign in the original binomial. If you recognize the pattern of the signs, it may help you memorize the patterns.
 The trinomial factor in the sum and difference of cubes pattern cannot be factored.
The trinomial factor in the sum and difference of cubes pattern cannot be factored.
It be very helpful if you learn to recognize the cubes of the integers from 1 to 10, just like you have learned to recognize squares. We have listed the cubes of the integers from 1 to 10 in [link].
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| {: valign=”top”} | ———- | |||||||||
| 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 | 1000 | {: valign=”top”}{: summary=”This table has 11 columns and 2 columns. The first column labels each row n and n cubed. The remaining columns of the first row have the numbers 1 through 10. The remaining columns of the second row have the numbers 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000.”}
Factor:
Factor:
Factor:
Is it a sum or difference?
Are the first and last terms perfect cubes?
Factor:
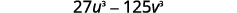 |
|
| This binomial is a difference. The first and last terms are perfect cubes. |
|
| Write the terms as cubes. | 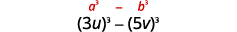 |
| Use the difference of cubes pattern. | 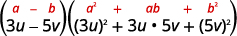 |
| Simplify. | 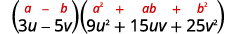 |
| Check by multiplying. | We’ll leave the check to you. |
Factor:
Factor:
In the next example, we first factor out the GCF. Then we can recognize the sum of cubes.
Factor:
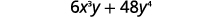 |
|
| Factor the common factor. | 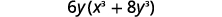 |
| This binomial is a sum The first and last terms are perfect cubes. |
|
| Write the terms as cubes. | 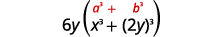 |
| Use the sum of cubes pattern. | 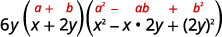 |
| Simplify. | 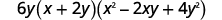 |
Check:
To check, you may find it easier to multiply the sum of cubes factors first, then multiply that product by
We’ll leave the multiplication for you.
Factor:
Factor:
The first term in the next example is a binomial cubed.
Factor:
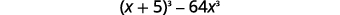 |
|
| This binomial is a difference. The first and last terms are perfect cubes. |
|
| Write the terms as cubes. | 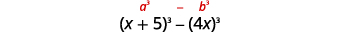 |
| Use the difference of cubes pattern. | 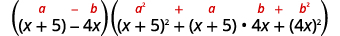 |
| Simplify. | 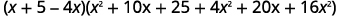 |
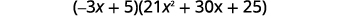 |
|
| Check by multiplying. | We’ll leave the check to you. |
Factor:
Factor:
Access this online resource for additional instruction and practice with factoring special products.
are real numbers,
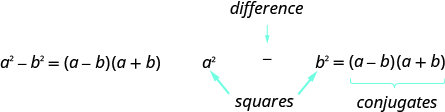
Is it a sum or difference?
Are the first and last terms perfect cubes?
Factor Perfect Square Trinomials
In the following exercises, factor completely using the perfect square trinomials pattern.
Factor Differences of Squares
In the following exercises, factor completely using the difference of squares pattern, if possible.
Factor Sums and Differences of Cubes
In the following exercises, factor completely using the sums and differences of cubes pattern, if possible.
Mixed Practice
In the following exercises, factor completely.
Why was it important to practice using the binomial squares pattern in the chapter on multiplying polynomials?
Answers will vary.
How do you recognize the binomial squares pattern?
Explain why
Use algebra, words, or pictures.
Answers will vary.
Maribel factored
as
Was she right or wrong? How do you know?
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
 ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?
ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?

You can also download for free at http://cnx.org/contents/02776133-d49d-49cb-bfaa-67c7f61b25a1@4.13
Attribution: