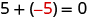 The missing number was the opposite of the number!
The missing number was the opposite of the number!By the end of this section, you will be able to:
A more thorough introduction to the topics covered in this section can be found in the Elementary Algebra chapter, Foundations.
The order we add two numbers doesn’t affect the result. If we add
or
the results are the same—they both equal 17. So,
The order in which we add does not matter!
Similarly, when multiplying two numbers, the order does not affect the result. If we multiply
or
the results are the same—they both equal 72. So,
The order in which we multiply does not matter!
These examples illustrate the Commutative Property.
When adding or multiplying, changing the order gives the same result.
The Commutative Property has to do with order. We subtract
and
, and see that
Since changing the order of the subtraction does not give the same result, we know that subtraction is not commutative.
Division is not commutative either. Since
changing the order of the division did not give the same result. The commutative properties apply only to addition and multiplication!
Addition and multiplication are commutative.
Subtraction and division are not commutative.
When adding three numbers, changing the grouping of the numbers gives the same result. For example,
since each side of the equation equals 17.
This is true for multiplication, too. For example,
since each side of the equation equals 5.
These examples illustrate the Associative Property.
When adding or multiplying, changing the grouping gives the same result.
The Associative Property has to do with grouping. If we change how the numbers are grouped, the result will be the same. Notice it is the same three numbers in the same order—the only difference is the grouping.
We saw that subtraction and division were not commutative. They are not associative either.
When simplifying an expression, it is always a good idea to plan what the steps will be. In order to combine like terms in the next example, we will use the Commutative Property of addition to write the like terms together.
Simplify:
Simplify:
Simplify:
When we have to simplify algebraic expressions, we can often make the work easier by applying the Commutative Property or Associative Property first.
Simplify:
Simplify:
Simplify:
What happens when we add 0 to any number? Adding 0 doesn’t change the value. For this reason, we call 0 the additive identity. The Identity Property of Addition that states that for any real number
and
What happens when we multiply any number by one? Multiplying by 1 doesn’t change the value. So we call 1 the multiplicative identity. The Identity Property of Multiplication that states that for any real number
and
We summarize the Identity Properties here.
What number added to 5 gives the additive identity, 0? We know
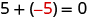 The missing number was the opposite of the number!
The missing number was the opposite of the number!
We call
the additive inverse of
The opposite of a number is its additive inverse. A number and its opposite add to zero, which is the additive identity. This leads to the Inverse Property of Addition that states for any real number
What number multiplied by
gives the multiplicative identity, 1? In other words,
times what results in 1? We know
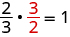 The missing number was the reciprocal of the number!
The missing number was the reciprocal of the number!
We call
the multiplicative inverse of a. The reciprocal of a number is its multiplicative inverse. This leads to the Inverse Property of Multiplication that states that for any real number
We’ll formally state the inverse properties here.
The Identity Property of addition says that when we add 0 to any number, the result is that same number. What happens when we multiply a number by 0? Multiplying by 0 makes the product equal zero.
What about division involving zero? What is
Think about a real example: If there are no cookies in the cookie jar and 3 people are to share them, how many cookies does each person get? There are no cookies to share, so each person gets 0 cookies. So,
We can check division with the related multiplication fact. So we know
because
Now think about dividing by zero. What is the result of dividing 4 by
Think about the related multiplication fact:
 Is there a number that multiplied by 0 gives
Is there a number that multiplied by 0 gives
Since any real number multiplied by 0 gives 0, there is no real number that can be multiplied by 0 to obtain 4. We conclude that there is no answer to
and so we say that division by 0 is undefined.
We summarize the properties of zero here.
Multiplication by Zero: For any real number a,
Division by Zero: For any real number a,
We will now practice using the properties of identities, inverses, and zero to simplify expressions.
Simplify:
Simplify:
Simplify:
Now we will see how recognizing reciprocals is helpful. Before multiplying left to right, look for reciprocals—their product is 1.
Simplify:
Simplify:
Simplify:
The next example makes us aware of the distinction between dividing 0 by some number or some number being divided by 0.
Simplify: ⓐ
where
ⓑ
where
ⓐ* * *
ⓑ* * *
Simplify: ⓐ
where
ⓑ
where
ⓐ 0 ⓑ undefined
Simplify: ⓐ
where
ⓑ
where
ⓐ 0 ⓑ undefined
Suppose that three friends are going to the movies. They each need $9.25—that’s 9 dollars and 1 quarter—to pay for their tickets. How much money do they need all together?
You can think about the dollars separately from the quarters. They need 3 times $9 so $27 and 3 times 1 quarter, so 75 cents. In total, they need $27.75. If you think about doing the math in this way, you are using the Distributive Property.
In algebra, we use the Distributive Property to remove parentheses as we simplify expressions.
Simplify:
Simplify:
Simplify:
Some students find it helpful to draw in arrows to remind them how to use the Distributive Property. Then the first step in [link] would look like this:
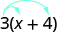 <div data-type="example">
<div data-type="example">
Simplify:
| | 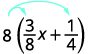 |
{: valign=”top”}| Distribute. |
|
{: valign=”top”}| Distribute. | 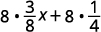 |
{: valign=”top”}| Multiply. |
|
{: valign=”top”}| Multiply. | 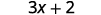 |
{: valign=”top”}{: .unnumbered .unstyled summary=”The expression is 8 open parentheses 3 by 8 x plus 1 by 4 close parentheses. There are arrows from 8 to 3 by 8 and 1 by 4. Distribute to get 8 into 3 by 8 x plus 8 into 1 by 4. Multiply to get 3x plus 2.” data-label=””}
|
{: valign=”top”}{: .unnumbered .unstyled summary=”The expression is 8 open parentheses 3 by 8 x plus 1 by 4 close parentheses. There are arrows from 8 to 3 by 8 and 1 by 4. Distribute to get 8 into 3 by 8 x plus 8 into 1 by 4. Multiply to get 3x plus 2.” data-label=””}
</div>
Simplify:
Simplify:
Using the Distributive Property as shown in the next example will be very useful when we solve money applications in later chapters.
Simplify:
| | 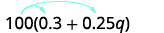 |
{: valign=”top”}| Distribute. |
|
{: valign=”top”}| Distribute. | 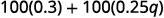 |
{: valign=”top”}| Multiply. |
|
{: valign=”top”}| Multiply. | 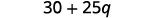 |
{: valign=”top”}{: .unnumbered .unstyled summary=”The expression is 100 open parentheses 0.3 plus 0.25q close parentheses. There are arrows from 100 to 0.3 and 0.25 q. Distribute to get 100 times 0.3 plus 100 times 0.25 q. Multiply to get 30 plus 25 q.” data-label=””}
|
{: valign=”top”}{: .unnumbered .unstyled summary=”The expression is 100 open parentheses 0.3 plus 0.25q close parentheses. There are arrows from 100 to 0.3 and 0.25 q. Distribute to get 100 times 0.3 plus 100 times 0.25 q. Multiply to get 30 plus 25 q.” data-label=””}
Simplify:
Simplify:
When we distribute a negative number, we need to be extra careful to get the signs correct!
Simplify:
Notice that you could also write the result as
Do you know why?
Simplify:
Simplify:
In the next example, we will show how to use the Distributive Property to find the opposite of an expression.
Simplify:
Simplify:
Simplify:
There will be times when we’ll need to use the Distributive Property as part of the order of operations. Start by looking at the parentheses. If the expression inside the parentheses cannot be simplified, the next step would be multiply using the Distributive Property, which removes the parentheses. The next two examples will illustrate this.
Simplify:
We follow the order of operations. Multiplication comes before subtraction, so we will distribute the 2 first and then subtract.
Simplify:
Simplify:
Simplify:
Simplify:
Simplify:
All the properties of real numbers we have used in this chapter are summarized here.
| Commutative Property When adding or multiplying, changing the order gives the same result |
| Associative Property When adding or multiplying, changing the grouping gives the same result. |
| Distributive Property |
| Identity Property |
| Inverse Property |
| Properties of Zero |
| Commutative Property When adding or multiplying, changing the order gives the same result |
| Associative Property When adding or multiplying, changing the grouping gives the same result. |
| Distributive Property |
| Identity Property |
| Inverse Property |
| Properties of Zero |
Use the Commutative and Associative Properties
In the following exercises, simplify.
Use the Properties of Identity, Inverse and Zero
In the following exercises, simplify.
where
0
where
where
undefined
where
where
undefined
where
Simplify Expressions Using the Distributive Property
In the following exercises, simplify using the Distributive Property.
In your own words, state the Associative Property of addition.
Answers will vary.
What is the difference between the additive inverse and the multiplicative inverse of a number?
Simplify
using the Distributive Property and explain each step.
Answers will vary.
Explain how you can multiply
without paper or calculator by thinking of
as
and then using the Distributive Property.
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
 ⓑ After reviewing this checklist, what will you do to become confident for all objectives?
ⓑ After reviewing this checklist, what will you do to become confident for all objectives?
Identify Multiples and Factors
Use the divisibility tests to determine whether 180 is divisible by 2, by 3, by 5, by 6, and by 10.
Divisible by
Find the prime factorization of 252.
Find the least common multiple of 24 and 40.
120
In the following exercises, simplify each expression.
4
Evaluate an Expression
In the following exercises, evaluate the following expressions.
When
ⓐ
ⓑ
ⓒ
when
3
Simplify Expressions by Combining Like Terms
In the following exercises, simplify the following expressions by combining like terms.
Translate an English Phrase to an Algebraic Expression
In the following exercises, translate the phrases into algebraic expressions.
ⓐ the sum of
and
ⓑ the product of
and
ⓒ twelve more than
ⓓ
less than
ⓐ eleven times the difference of
and two* * *
ⓑ the difference of eleven times
and two
ⓐ
ⓑ
Dushko has nickels and pennies in his pocket. The number of pennies is four less than five the number of nickels. Let
represent the number of nickels. Write an expression for the number of pennies.
Simplify Expressions with Absolute Value
In the following exercise, fill in
or
for each of the following pairs of numbers.
ⓐ
ⓑ
ⓒ
ⓓ
ⓐ
ⓑ
ⓒ
ⓓ
In the following exercises, simplify.
Add and Subtract Integers
In the following exercises, simplify each expression.
ⓐ
ⓑ
ⓒ
ⓓ
ⓐ 8 ⓑ
ⓒ
ⓓ 22
ⓐ
ⓑ
ⓐ 40 ⓑ 40
Multiply and Divide Integers
In the following exercise, multiply or divide.
ⓐ
ⓑ
ⓒ
ⓓ
ⓐ
ⓑ
ⓒ
ⓓ 17
Simplify and Evaluate Expressions with Integers
In the following exercises, simplify each expression.
ⓐ
ⓑ
16
For the following exercises, evaluate each expression.
when* * *
9
when* * *
Translate English Phrases to Algebraic Expressions
In the following exercises, translate to an algebraic expression and simplify if possible.
the sum of
and
increased by 23
ⓐ the difference of 17 and
ⓑ subtract 17 from
Use Integers in Applications
In the following exercise, solve.
Temperature On July 10, the high temperature in Phoenix, Arizona, was 109°, and the high temperature in Juneau, Alaska, was 63°. What was the difference between the temperature in Phoenix and the temperature in Juneau?
Simplify Fractions
In the following exercises, simplify.
Multiply and Divide Fractions
In the following exercises, perform the indicated operation.
Add and Subtract Fractions
In the following exercises, perform the indicated operation.
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ
ⓑ
Use the Order of Operations to Simplify Fractions
In the following exercises, simplify.
75
Evaluate Variable Expressions with Fractions
In the following exercises, evaluate.
when* * *
and
when* * *
Round Decimals
Round
to the nearest ⓐ hundredth ⓑ tenth ⓒ whole number.
Add and Subtract Decimals
In the following exercises, perform the indicated operation.
Multiply and Divide Decimals
In the following exercises, perform the indicated operation.
488.1813
Convert Decimals, Fractions and Percents
In the following exercises, write each decimal as a fraction.
In the following exercises, convert each fraction to a decimal.
In the following exercises, convert each decimal to a percent.
Simplify Expressions with Square Roots
In the following exercises, simplify.
no real number
Identify Integers, Rational Numbers, Irrational Numbers, and Real Numbers
In the following exercise, list the ⓐ whole numbers ⓑ integers ⓒ rational numbers ⓓ irrational numbers ⓔ real numbers for each set of numbers
Locate Fractions and Decimals on the Number Line
In the following exercises, locate the numbers on a number line.
ⓐ
ⓑ
Use the Commutative and Associative Properties
In the following exercises, simplify.
Use the Properties of Identity, Inverse and Zero
In the following exercises, simplify.
undefined
Simplify Expressions Using the Distributive Property
In the following exercises, simplify using the Distributive Property.
Find the prime factorization of
Combine like terms:
Evaluate when
and
Translate to an algebraic expression and simplify:
ⓐ eleven less than negative eight
ⓑ the difference of
and
, increased by 5
Dushko has nickels and pennies in his pocket. The number of pennies is seven less than four times the number of nickels. Let
represent the number of nickels. Write an expression for the number of pennies.
Round
to the nearest
ⓐ hundredth ⓑ thousandth
ⓐ
ⓑ
Convert
ⓐ
to a decimal ⓑ
to a percent
Locate
on a number line.
In the following exercises, simplify each expression.
1
160
ⓐ
ⓑ
ⓐ 0 ⓑ undefined

You can also download for free at http://cnx.org/contents/02776133-d49d-49cb-bfaa-67c7f61b25a1@4.13
Attribution: