 Similarly, a multiple of 3 would be the product of a counting number and 3.
Similarly, a multiple of 3 would be the product of a counting number and 3.By the end of this section, you will be able to:
This chapter is intended to be a brief review of concepts that will be needed in an Intermediate Algebra course. A more thorough introduction to the topics covered in this chapter can be found in the Elementary Algebra chapter, Foundations.
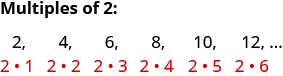
The numbers 2, 4, 6, 8, 10, 12 are called multiples of 2. A multiple of 2 can be written as the product of a counting number and 2.
 Similarly, a multiple of 3 would be the product of a counting number and 3.
Similarly, a multiple of 3 would be the product of a counting number and 3.
 We could find the multiples of any number by continuing this process.
We could find the multiples of any number by continuing this process.
| Counting Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | {: valign=”top”}|———- | Multiples of 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | {: valign=”top”}| Multiples of 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | {: valign=”top”}| Multiples of 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | {: valign=”top”}| Multiples of 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | {: valign=”top”}| Multiples of 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | {: valign=”top”}| Multiples of 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | {: valign=”top”}| Multiples of 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | {: valign=”top”}| Multiples of 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | {: valign=”top”}{: .unnumbered summary=”This table has 13 columns, 8 rows and a header row. The header row labels each column: counting number, 1, 2, 3, 4, 5, 6, 7, 8, 9. The first column labels each row: multiples of 2, multiples of 3, multiples of 4, multiples of 5, multiples of 6, multiples of 7, multiples of 8, multiples of 9. The column labeled 1 has the following values: 2, 3, 4, 5, 6, 7, 8, 9. The column labeled 2 has the following values: 4, 6, 8, 10, 12, 14, 16, 18. The column labeled 3 has the following values: 6, 9, 12, 15, 18, 21, 24, 27. The column labeled 4 has the following values: 8, 12, 16, 20, 24, 28, 32, 36. The column labeled 5 has the following values: 10, 15, 20, 25, 30, 35, 40, 45. The column labeled 6 has the following values: 12, 18, 24, 30, 36, 42, 48, 54. The column labeled 7 has the following values: 14, 21, 28, 35, 42, 49, 56, 63. The column labeled 8 has the following values: 16, 24, 32, 40, 48, 56, 64, 72. The column labeled 9 has the following values: 18, 27, 36, 45, 54, 63, 72, 81. The column labeled 10 has the following values: 20, 30, 40, 50, 60, 70, 80, 90. The column labeled 11 has the following values: 22, 33, 44, 55, 66, 77, 88, 99. The column labeled 12 has the following values: 24, 36, 48, 60, 72, 84, 96, 108.”}
A number is a multiple of
if it is the product of a counting number and
Another way to say that 15 is a multiple of 3 is to say that 15 is divisible by 3. That means that when we divide 3 into 15, we get a counting number. In fact,
is 5, so 15 is
If a number
is a multiple of n, then m is divisible by n.
If we were to look for patterns in the multiples of the numbers 2 through 9, we would discover the following divisibility tests:
A number is divisible by:
2 if the last digit is 0, 2, 4, 6, or 8.
3 if the sum of the digits is divisible by
5 if the last digit is 5 or
6 if it is divisible by both 2 and
10 if it ends with
Is 5,625 divisible by ⓐ 2? ⓑ 3? ⓒ 5 or 10? ⓓ 6?
Is 4,962 divisible by ⓐ 2? ⓑ 3? ⓒ 5? ⓓ 6? ⓔ 10?
ⓐ yes ⓑ yes ⓒ no ⓓ yes* * *
ⓔ no
Is 3,765 divisible by ⓐ 2? ⓑ 3? ⓒ 5? ⓓ 6? ⓔ 10?
ⓐ no ⓑ yes ⓒ yes ⓓ no* * *
ⓔ no
In mathematics, there are often several ways to talk about the same ideas. So far, we’ve seen that if m is a multiple of n, we can say that m is divisible by n. For example, since 72 is a multiple of 8, we say 72 is divisible by 8. Since 72 is a multiple of 9, we say 72 is divisible by 9. We can express this still another way.
Since
we say that 8 and 9 are factors of 72. When we write
we say we have factored 72.
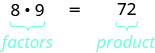 Other ways to factor 72 are
Other ways to factor 72 are
and
The number 72 has many factors:
and
If
then a and b are factors of m.
Some numbers, such as 72, have many factors. Other numbers have only two factors. A prime number is a counting number greater than 1 whose only factors are 1 and itself.
A prime number is a counting number greater than 1 whose only factors are 1 and the number itself.
A composite number is a counting number that is not prime. A composite number has factors other than 1 and the number itself.
The counting numbers from 2 to 20 are listed in the table with their factors. Make sure to agree with the “prime” or “composite” label for each!
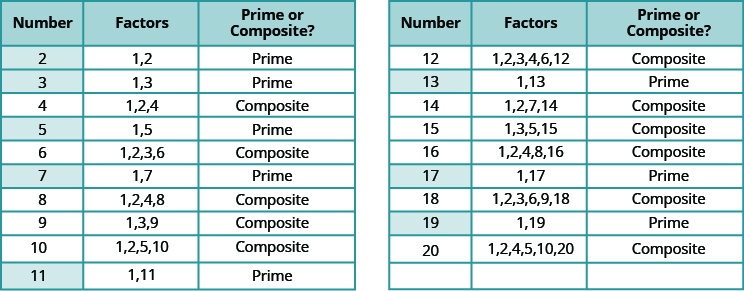 The prime numbers less than 20 are 2, 3, 5, 7, 11, 13, 17, and 19. Notice that the only even prime number is 2.
The prime numbers less than 20 are 2, 3, 5, 7, 11, 13, 17, and 19. Notice that the only even prime number is 2.
A composite number can be written as a unique product of primes. This is called the prime factorization of the number. Finding the prime factorization of a composite number will be useful in many topics in this course.
The prime factorization of a number is the product of prime numbers that equals the number.
To find the prime factorization of a composite number, find any two factors of the number and use them to create two branches. If a factor is prime, that branch is complete. Circle that prime. Otherwise it is easy to lose track of the prime numbers.
If the factor is not prime, find two factors of the number and continue the process. Once all the branches have circled primes at the end, the factorization is complete. The composite number can now be written as a product of prime numbers.
Factor 48.




We say
is the prime factorization of 48. We generally write the primes in ascending order. Be sure to multiply the factors to verify your answer.
If we first factored 48 in a different way, for example as
the result would still be the same. Finish the prime factorization and verify this for yourself.
Find the prime factorization of
Find the prime factorization of
One of the reasons we look at primes is to use these techniques to find the least common multiple of two numbers. This will be useful when we add and subtract fractions with different denominators.
The least common multiple (LCM) of two numbers is the smallest number that is a multiple of both numbers.
To find the least common multiple of two numbers we will use the Prime Factors Method. Let’s find the LCM of 12 and 18 using their prime factors.
Find the least common multiple (LCM) of 12 and 18 using the prime factors method.
Notice that the prime factors of 12
and the prime factors of 18
are included in the LCM
So 36 is the least common multiple of 12 and 18.
By matching up the common primes, each common prime factor is used only once. This way you are sure that 36 is the least common multiple.
Find the LCM of 9 and 12 using the Prime Factors Method.
Find the LCM of 18 and 24 using the Prime Factors Method.
In algebra, we use a letter of the alphabet to represent a number whose value may change. We call this a variable and letters commonly used for variables are
A variable is a letter that represents a number whose value may change.
A number whose value always remains the same is called a constant.
A constant is a number whose value always stays the same.
To write algebraically, we need some operation symbols as well as numbers and variables. There are several types of symbols we will be using. There are four basic arithmetic operations: addition, subtraction, multiplication, and division. We’ll list the symbols used to indicate these operations below.
| Operation | Notation | Say: | The result is… |
|---|---|---|---|
| Addition | plus | the sum of and | |
| Subtraction | minus | the difference of and | |
| Multiplication | times | the product of and | |
| Division | divided by | the quotient of and is called the dividend, and is called the divisor |
When two quantities have the same value, we say they are equal and connect them with an equal sign.
is read “a is equal to b.”
The symbol “=” is called the equal sign.
On the number line, the numbers get larger as they go from left to right. The number line can be used to explain the symbols “<” and “>”.
The expressions
or
can be read from left to right or right to left, though in English we usually read from left to right. In general,
| Inequality Symbols | Words | {: valign=”top”}|———- |
| a is not equal to b. | |
| {: valign=”top”} |
| a is less than b. | |
| {: valign=”top”} |
| a is less than or equal to b. | |
| {: valign=”top”} |
| a is greater than b. | |
| {: valign=”top”} |
| a is greater than or equal to b. | {: valign=”top”}{: .unnumbered summary=”The table describes inequality symbols in words. The symbols described are a is not equal to b, a is less than b, a is less than or equal to b, a is greater then b, a is greater than or equal to b.”}
Grouping symbols in algebra are much like the commas, colons, and other punctuation marks in English. They help identify an expression, which can be made up of number, a variable, or a combination of numbers and variables using operation symbols. We will introduce three types of grouping symbols now.
Here are some examples of expressions that include grouping symbols. We will simplify expressions like these later in this section.
What is the difference in English between a phrase and a sentence? A phrase expresses a single thought that is incomplete by itself, but a sentence makes a complete statement. A sentence has a subject and a verb. In algebra, we have expressions and equations.
An expression is a number, a variable, or a combination of numbers and variables using operation symbols.
Notice that the English phrases do not form a complete sentence because the phrase does not have a verb.
An equation is two expressions linked by an equal sign. When you read the words the symbols represent in an equation, you have a complete sentence in English. The equal sign gives the verb.
An equation is two expressions connected by an equal sign.
Suppose we need to multiply 2 nine times. We could write this as
This is tedious and it can be hard to keep track of all those 2s, so we use exponents. We write
as
and
as
In expressions such as
the 2 is called the base and the 3 is called the exponent. The exponent tells us how many times we need to multiply the base.
 <div data-type="note" markdown="1">
<div data-type="note" markdown="1">
We say
is in exponential notation and
is in expanded notation.
means multiply a by itself, n times.
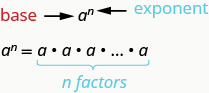 The expression
The expression
is read a to the
power.
</div>
While we read
as
to the
power”, we usually read:
We’ll see later why
and
have special names.
[link] shows how we read some expressions with exponents.
| Expression | In Words | | {: valign=”top”}|———- | 72 | 7 to the second power or | 7 squared | {: valign=”top”}| 53 | 5 to the third power or | 5 cubed | {: valign=”top”}| 94 | 9 to the fourth power | | {: valign=”top”}| 125 | 12 to the fifth power | | {: valign=”top”}{: summary=”This table shows four expressions and words to describe these. The expressions described are 7 to the second power or 7 squared, 5 to the third power or 5 cubed, 9 to the fourth power and 12 to the fifth.”}
To simplify an expression means to do all the math possible. For example, to simplify
we would first multiply
to get 8 and then add the 1 to get 9. A good habit to develop is to work down the page, writing each step of the process below the previous step. The example just described would look like this:
By not using an equal sign when you simplify an expression, you may avoid confusing expressions with equations.
To simplify an expression, do all operations in the expression.
We’ve introduced most of the symbols and notation used in algebra, but now we need to clarify the order of operations. Otherwise, expressions may have different meanings, and they may result in different values.
For example, consider the expression
Some students simplify this getting 49, by adding
and then multiplying that result by 7. Others get 25, by multiplying
first and then adding 4.
The same expression should give the same result. So mathematicians established some guidelines that are called the order of operations.
Students often ask, “How will I remember the order?” Here is a way to help you remember: Take the first letter of each key word and substitute the silly phrase “Please Excuse My Dear Aunt Sally”.
It’s good that “My Dear” goes together, as this reminds us that multiplication and division have equal priority. We do not always do multiplication before division or always do division before multiplication. We do them in order from left to right.
Similarly, “Aunt Sally” goes together and so reminds us that addition and subtraction also have equal priority and we do them in order from left to right.
Simplify:
| | 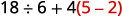 |
{: valign=”top”}| Parentheses? Yes, subtract first. |
|
{: valign=”top”}| Parentheses? Yes, subtract first. | 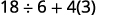 |
{: valign=”top”}| Exponents? No. | |
{: valign=”top”}| Multiplication or division? Yes. | |
{: valign=”top”}| Divide first because we multiply and divide left to right. |
|
{: valign=”top”}| Exponents? No. | |
{: valign=”top”}| Multiplication or division? Yes. | |
{: valign=”top”}| Divide first because we multiply and divide left to right. | 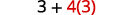 |
{: valign=”top”}| Any other multiplication or division? Yes. | |
{: valign=”top”}| Multiply. |
|
{: valign=”top”}| Any other multiplication or division? Yes. | |
{: valign=”top”}| Multiply. |  |
{: valign=”top”}| Any other multiplication of division? No. | |
{: valign=”top”}| Any addition or subtraction? Yes. | |
{: valign=”top”}| Add. |
|
{: valign=”top”}| Any other multiplication of division? No. | |
{: valign=”top”}| Any addition or subtraction? Yes. | |
{: valign=”top”}| Add. | 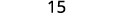 |
{: valign=”top”}{: .unnumbered .unstyled .can-break summary=”The expression is 18 divided by 6 plus 4 open parentheses 5 minus 2 close parentheses. Since there are parentheses, we first open them by performing the subtraction 5 minus 2. The expression now is 18 divided by 6 plus 4 times 3. There are no exponents. Next we check for multiplication and division. Divide first because we multiply and divide left to right. We now have 3 plus 4 times 3. Next we multiply. We now have 3 plus 12. There is no other multiplication or division. Finally, we check for addition or subtraction. We add to get the number 15.” data-label=””}
|
{: valign=”top”}{: .unnumbered .unstyled .can-break summary=”The expression is 18 divided by 6 plus 4 open parentheses 5 minus 2 close parentheses. Since there are parentheses, we first open them by performing the subtraction 5 minus 2. The expression now is 18 divided by 6 plus 4 times 3. There are no exponents. Next we check for multiplication and division. Divide first because we multiply and divide left to right. We now have 3 plus 4 times 3. Next we multiply. We now have 3 plus 12. There is no other multiplication or division. Finally, we check for addition or subtraction. We add to get the number 15.” data-label=””}
Simplify:
16
Simplify:
23
When there are multiple grouping symbols, we simplify the innermost parentheses first and work outward.
Simplify:
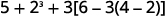 |
|
| Are there any parentheses (or other grouping symbols)? Yes. |
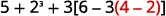 |
| Focus on the parentheses that are inside the brackets. Subtract. |
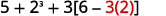 |
| Continue inside the brackets and multiply. | 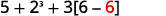 |
| Continue inside the brackets and subtract. |  |
| The expression inside the brackets requires no further simplification. |
|
| Are there any exponents? Yes. Simplify exponents. |  |
| Is there any multiplication or division? Yes. | |
| Multiply. |  |
| Is there any addition of subtraction? Yes. | |
| Add. | 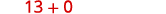 |
| Add. |  |
Simplify:
86
Simplify:
1
In the last few examples, we simplified expressions using the order of operations. Now we’ll evaluate some expressions—again following the order of operations. To evaluate an expression means to find the value of the expression when the variable is replaced by a given number.
To evaluate an expression means to find the value of the expression when the variable is replaced by a given number.
To evaluate an expression, substitute that number for the variable in the expression and then simplify the expression.
Evaluate when
ⓐ
ⓑ
ⓒ
ⓐ* * *
| | | | 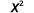 |
{: valign=”top”}|
|
{: valign=”top”}| 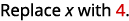 | | |
| | |  |
{: valign=”top”}| Use definition of exponent. | | |
|
{: valign=”top”}| Use definition of exponent. | | | 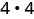 |
{: valign=”top”}| Simplify. | | |
|
{: valign=”top”}| Simplify. | | | 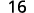 |
{: valign=”top”}{: .unnumbered .unstyled summary=”The expression is x squared. Replace x with 4 to get 4 squared. Use definition of exponent to get 4 times 4. Simplify to get 16.” data-label=””}
|
{: valign=”top”}{: .unnumbered .unstyled summary=”The expression is x squared. Replace x with 4 to get 4 squared. Use definition of exponent to get 4 times 4. Simplify to get 16.” data-label=””}
ⓑ* * *
| | | 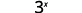 |
{: valign=”top”}|
|
{: valign=”top”}| 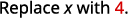 | |
| |  |
{: valign=”top”}| Use definition of exponent. | |
|
{: valign=”top”}| Use definition of exponent. | |  |
{: valign=”top”}| Simplify. | |
|
{: valign=”top”}| Simplify. | | 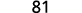 |
{: valign=”top”}{: .unnumbered .unstyled summary=”The expression is 3 raised to the power x. Replace x with 4 to get 3 to the power 4. Use definition of exponent to get 3 times 3 times 3 times 3. Simplify to get 81.” data-label=””}
|
{: valign=”top”}{: .unnumbered .unstyled summary=”The expression is 3 raised to the power x. Replace x with 4 to get 3 to the power 4. Use definition of exponent to get 3 times 3 times 3 times 3. Simplify to get 81.” data-label=””}
ⓒ* * *
| | 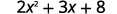 |
{: valign=”top”}|
|
{: valign=”top”}| 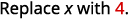 |
| 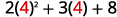 |
{: valign=”top”}| Follow the order of operations. |
|
{: valign=”top”}| Follow the order of operations. | 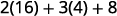 |
{: valign=”top”}| |
|
{: valign=”top”}| | 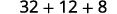 |
{: valign=”top”}| |
|
{: valign=”top”}| | 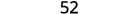 |
{: valign=”top”}{: .unnumbered .unstyled summary=”The expression is 2 x squared plus 3 x plus 8. Substitute x with 4 to get 2 open parentheses 4 close parentheses squared plus 3 open parentheses 4 close parentheses plus 8. Follow order of operations to first get 2 open parentheses 16 close parentheses plus 3 open parentheses 4 close parentheses plus 8. Then, 32 plus 12 plus 8. Then, 52.” data-label=””}
|
{: valign=”top”}{: .unnumbered .unstyled summary=”The expression is 2 x squared plus 3 x plus 8. Substitute x with 4 to get 2 open parentheses 4 close parentheses squared plus 3 open parentheses 4 close parentheses plus 8. Follow order of operations to first get 2 open parentheses 16 close parentheses plus 3 open parentheses 4 close parentheses plus 8. Then, 32 plus 12 plus 8. Then, 52.” data-label=””}
Evaluate when
ⓐ
ⓑ
ⓒ
ⓐ 9 ⓑ 64 ⓒ40
Evaluate when
ⓐ
ⓑ
ⓒ
ⓐ 216 ⓑ 64 ⓒ 185
Algebraic expressions are made up of terms. A term is a constant, or the product of a constant and one or more variables.
A term is a constant or the product of a constant and one or more variables.
Examples of terms are
and
The constant that multiplies the variable is called the coefficient.
The coefficient of a term is the constant that multiplies the variable in a term.
Think of the coefficient as the number in front of the variable. The coefficient of the term
is 3. When we write
the coefficient is 1, since
Some terms share common traits. When two terms are constants or have the same variable and exponent, we say they are like terms.
Look at the following 6 terms. Which ones seem to have traits in common?
We say,
and
are like terms.
and
are like terms.
and
are like terms.
Terms that are either constants or have the same variables raised to the same powers are called like terms.
If there are like terms in an expression, you can simplify the expression by combining the like terms. We add the coefficients and keep the same variable.
Simplify:
Simplify:
Simplify:
We listed many operation symbols that are used in algebra. Now, we will use them to translate English phrases into algebraic expressions. The symbols and variables we’ve talked about will help us do that. [link] summarizes them.
| Operation | Phrase | Expression |
|---|---|---|
| Addition | a plus b the sum of and b a increased by b b more than a the total of a and b b added to a |
|
| Subtraction | a minus the difference of a and b a decreased by b b less than a b subtracted from a |
|
| Multiplication | a times b the product of and twice a |
|
| Division | a divided by b the quotient of a and b the ratio of a and b b divided into a |
Look closely at these phrases using the four operations:
 Each phrase tells us to operate on two numbers. Look for the words of and and to find the numbers.
Each phrase tells us to operate on two numbers. Look for the words of and and to find the numbers.
Translate each English phrase into an algebraic expression:
ⓐ the difference of
and 9* * *
ⓑ the quotient of
and 3* * *
ⓒ twelve more than
ⓓ seven less than
ⓐ The key word is difference, which tells us the operation is subtraction. Look for the words of and and to find the numbers to subtract.
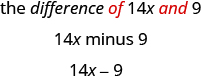 ⓑ The key word is quotient, which tells us the operation is division.
ⓑ The key word is quotient, which tells us the operation is division.
 ⓒ The key words are more than. They tell us the operation is addition. More than means “added to.”
ⓒ The key words are more than. They tell us the operation is addition. More than means “added to.”
ⓓ The key words are less than. They tell us to subtract. Less than means “subtracted from.”
Translate the English phrase into an algebraic expression:
ⓐ the difference of
and 13* * *
ⓑ the quotient of
and 2* * *
ⓒ 13 more than
ⓓ 18 less than
ⓐ
ⓑ
ⓒ
ⓓ
Translate the English phrase into an algebraic expression:
ⓐ the sum of
and 19* * *
ⓑ the product of
and *y** * *
ⓒ Eleven more than *x** * *
ⓓ Fourteen less than 11a
ⓐ
ⓑ
ⓒ
ⓓ
We look carefully at the words to help us distinguish between multiplying a sum and adding a product.
Translate the English phrase into an algebraic expression:
ⓐ eight times the sum of x and *y** * *
ⓑ the sum of eight times x and y
There are two operation words—times tells us to multiply and sum tells us to add.
ⓐ Because we are multiplying 8 times the sum, we need parentheses around the sum of x and y,
This forces us to determine the sum first. (Remember the order of operations.)
ⓑ To take a sum, we look for the words of and and to see what is being added. Here we are taking the sum of eight times x and y.
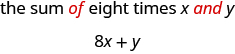
Translate the English phrase into an algebraic expression:
ⓐ four times the sum of p and *q** * *
ⓑ the sum of four times p and q
ⓐ
ⓑ
Translate the English phrase into an algebraic expression:
ⓐ the difference of two times x and 8* * *
ⓑ two times the difference of x and 8
ⓐ
ⓑ
Later in this course, we’ll apply our skills in algebra to solving applications. The first step will be to translate an English phrase to an algebraic expression. We’ll see how to do this in the next two examples.
The length of a rectangle is 14 less than the width. Let w represent the width of the rectangle. Write an expression for the length of the rectangle.
The length of a rectangle is 7 less than the width. Let w represent the width of the rectangle. Write an expression for the length of the rectangle.
The width of a rectangle is 6 less than the length. Let l represent the length of the rectangle. Write an expression for the width of the rectangle.
The expressions in the next example will be used in the typical coin mixture problems we will see soon.
June has dimes and quarters in her purse. The number of dimes is seven less than four times the number of quarters. Let q represent the number of quarters. Write an expression for the number of dimes.
Geoffrey has dimes and quarters in his pocket. The number of dimes is eight less than four times the number of quarters. Let q represent the number of quarters. Write an expression for the number of dimes.
Lauren has dimes and nickels in her purse. The number of dimes is three more than seven times the number of nickels. Let n represent the number of nickels. Write an expression for the number of dimes.
A number is divisible by:
2 if the last digit is 0, 2, 4, 6, or 8.
3 if the sum of the digits is divisible by 3.
5 if the last digit is 5 or 0.
6 if it is divisible by both 2 and 3.
10 if it ends with 0.
is read “a is equal to b.”
The symbol “=” is called the equal sign.

| Inequality Symbols | Words |
| {: valign=”top”} | ———- |
| a is not equal to b. | |
| {: valign=”top”} |
| a is less than b. | |
| {: valign=”top”} |
| a is less than or equal to b. | |
| {: valign=”top”} |
| a is greater than b. | |
| {: valign=”top”} |
| a is greater than or equal to b. | {: valign=”top”}{: summary=”The table describes inequality symbols in words. The symbols described are a is not equal to b, a is less than b, a is less than or equal to b, a is greater then b, a is greater than or equal to b.”}
means multiply a by itself, n times.
The expression
is read a to the
power.
To simplify an expression, do all operations in the expression.
| Operation | Phrase | Expression |
|---|---|---|
| Addition | a plus b the sum of and b a increased by b b more than a the total of a and b b added to a |
|
| Subtraction | a minus the difference of a and b a decreased by b b less than a b subtracted from a |
|
| Multiplication | a times b the product of and twice a |
|
| Division | a divided by b the quotient of a and b the ratio of a and b b divided into a |
Identify Multiples and Factors
In the following exercises, use the divisibility tests to determine whether each number is divisible by 2, by 3, by 5, by 6, and by 10.
84
Divisible by 2, 3, 6
96
896
Divisible by 2
942
22,335
Divisible by 3, 5
39,075
Find Prime Factorizations and Least Common Multiples
In the following exercises, find the prime factorization.
86
78
455
400
432
627
In the following exercises, find the least common multiple of each pair of numbers using the prime factors method.
8, 12
24
12, 16
28, 40
420
84, 90
55, 88
440
60, 72
Simplify Expressions Using the Order of Operations
In the following exercises, simplify each expression.
5
58
29
149
50
5
Evaluate an Expression
In the following exercises, evaluate the following expressions.
When
ⓐ
ⓑ
ⓒ
ⓐ 64 ⓑ 16 ⓒ 7
When
ⓐ
ⓑ
ⓒ
When
21
When
When
9
When
Simplify Expressions by Combining Like Terms
In the following exercises, simplify the following expressions by combining like terms.
Translate an English Phrase to an Algebraic Expression
In the following exercises, translate the phrases into algebraic expressions.
ⓐ the difference of
and
ⓑ the quotient of
and
ⓒ Twenty-one more than
ⓓ
less than
ⓐ
ⓑ
ⓒ
ⓓ
ⓐ the difference of
and
ⓑ the quotient of
and
ⓒ Eighteen more than
;* * *
ⓓ
less than
ⓐ the sum of
and
ⓑ the product of
and
ⓒ Fifteen more than
ⓓ
less than
ⓐ
ⓑ
ⓒ
ⓓ
ⓐ the sum of
and
ⓑ the product of
and
ⓒ Twelve more than
ⓓ
less than
ⓐ eight times the difference of
and nine* * *
ⓑ the difference of eight times
and 9
ⓐ
ⓑ
ⓐ seven times the difference of
and one* * *
ⓑ the difference of seven times
and 1
ⓐ five times the sum of
and
ⓑ the sum of five times
and
ⓐ
ⓑ
ⓐ eleven times the sum of
and
ⓑ the sum of eleven times
and
Eric has rock and country songs on his playlist. The number of rock songs is 14 more than twice the number of country songs. Let c represent the number of country songs. Write an expression for the number of rock songs.
The number of women in a Statistics class is 8 more than twice the number of men. Let
represent the number of men. Write an expression for the number of women.
Greg has nickels and pennies in his pocket. The number of pennies is seven less than three the number of nickels. Let n represent the number of nickels. Write an expression for the number of pennies.
Jeannette has
and
bills in her wallet. The number of fives is three more than six times the number of tens. Let
represent the number of tens. Write an expression for the number of fives.
Explain in your own words how to find the prime factorization of a composite number.
Answers will vary.
Why is it important to use the order of operations to simplify an expression?
Explain how you identify the like terms in the expression
Answers will vary.
Explain the difference between the phrases “4 times the sum of x and y” and “the sum of 4 times x and y”.
ⓐ Use this checklist to evaluate your mastery of the objectives of this section.
 ⓑ If most of your checks were:
ⓑ If most of your checks were:
…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.
…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no - I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.
then a and b are factors of m.

You can also download for free at http://cnx.org/contents/02776133-d49d-49cb-bfaa-67c7f61b25a1@4.13
Attribution: